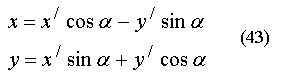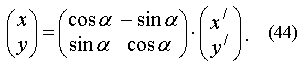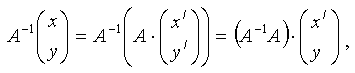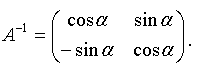- •44) Основные особенности ос unix
- •45) Принципы реализации ос реального времени
- •Отличия от операционных систем общего назначения
- •Выполнение задачи
- •Алгоритмы планирования
- •Взаимодействие между задачами и разделение ресурсов
- •46) Микроядерные и микроядерные ос. Qnx пример микроядерной ос
- •47) Архитектура Ос класса Windows nt
- •Режим пользователя
- •Режим ядра
- •48) Понятие контекста устройства windows
- •49) Основные графические примитивы windows
- •50) Физическая и логическая системы координат графического приложения
- •51) Преобразование систем координат: параллельный перенос, поворот. Поняие однородной системы координат
- •Проективная геометрия[править | править исходный текст]
- •Растровая и векторная графика
- •Растровая графика
- •53) Управление как процесс, функции управления.
- •54) Эволюция управления как научной дисциплины. Школы менеджмента.
- •55) Системный подход к управлению. Сущность подхода.
- •56) Ситуационный подход к управлению. Методология подхода.
- •57) Внешняя и внутренняя среда организации. Факторы прямого и косвенного воздействия. Характеристики внешней среды. Взаимосвязь факторов внутренней среды.
- •58) Коммуникации как связующая функция управления. Виды коммуникации. Эффективность коммуникации.
- •59) Принятие решений как связующая функция управления. Виды решений. Этапы рационального решения.
- •60) Стратегическое планирование. Миссия и стратегия организации. Виды стратегии.
- •61) Организация как функция управления. Делегирование полномочий. Виды полномочий.
- •62) Организационная структура. Бюрократические и адаптивные организационные структуры.
- •63) Контроль. Виды Контроля. Характеристики эффективного контроля.
- •64) Лидерство. Основные подходы к лидерству.
- •65) Прикладные механизмы платформы 1с:Предприятие.
- •66) Механизм бухгалтерского учёта в платформе 1с: Предприятие
- •67) Основные инструменты администрирования системы 1с: Предприятие.
49) Основные графические примитивы windows
System.Drawing, Graphics.
Класс Graphics предоставляет методы для вывода объектов в устройстве отображения. Объект Graphics связан с конкретным контекстом устройства.
Используя объект Graphics, можно нарисовать много разных фигур и линий. Дополнительные сведения о рисовании линий и фигур см. в описании метода Draw графического элемента для линии или фигуры, которую требуется нарисовать. К этим методам относятся DrawLine,DrawArc, DrawClosedCurve, DrawPolygon и DrawRectangle. Дополнительные сведения о рисовании линий и фигур см. в разделах Рисование линий и фигур с помощью пера и Использование кисти для заливки фигур.
Рисунки и значки можно также рисовать с помощью методов DrawImage иDrawIcon, соответственно. Чтобы выполнить передачу данных о цвете блоками битов с экрана на поверхность рисования объекта Graphics, см.CopyFromScreen. Дополнительные сведения о рисовании рисунков с помощью объекта Graphics см. в разделе Работа с растровыми и векторными изображениями.
Кроме того, можно манипулировать системой координат, используемой объектом Graphics. Дополнительные сведения о системе координат и манипуляциях с ней см. в разделе Системы координат и преобразования.
50) Физическая и логическая системы координат графического приложения
Физическая система координат представляет собой матрицу пикселов фиксированной ширины и высоты. Начало координат находится в левом верхнем углу. Ось X направлена слева направо, а ось Y— сверху вниз. Максимальный размер физического устройства равен 227 х 227 пикселов. Для дисплея физические координаты называют также экранными координатами1. Экранные координаты обычно используются в операциях управления окнами. Например, функция GetWindowRect возвращает ограничивающий прямоугольник окна в экранных координатах. Также экранные координаты содержатся в параметрах таких сообщений, как WM_NCM0USEM0VE. Это сообщение генерируется при перемещении курсора мыши в пределах неклиентской част окна. Следует учитывать, что бывают случаи, когда не все пикселы физической по верхности могут отображаться устройством. Например, для принтеров существу ют механические ограничения, не позволяющие печатать у краев страниц. В та ких ситуациях приложение должно получить информацию об отображаемой част! поверхности при помощи функции GetDeviceCap.
Логическая система координат во многих случаях позволяет создавать приложения, независимые от конкретного типа устройства графического вывода.
Для указания режима отображения в файле windows.h определены символьные константы с префиксом MM_. При создании контекста устройства по умолчанию устанавливается режим отображения MM_TEXT. В этом режиме используется логическая система координат, полностью эквивалентная физической. Каждая единица по оси x или у соответствует одному пикселю экрана.
51) Преобразование систем координат: параллельный перенос, поворот. Поняие однородной системы координат
|
Параллельный перенос системы координат | |
|
Однородные координаты ― координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же ненулевое число.