1.10. Метод логарифмического дифференцирования
Функцию вида
y =[u(x)]v(x) , где u(x)>0, |
(8) |
в том случае, когда основание и показатель являются функциями от x, называют степенно-показательной.
Чтобы найти производную от этой функции, сначала прологарифмируем равенство (8), а затем найдём производную полученной неявно заданной функции.
Пример 29. Найти производную степенно-показательной функции
y = (x2 + 1)sinx.
Решение.
Прологарифмируем данное равенство: lny = ln(x2 + 1)sinx ,
lny = sinx·ln(x 2 + 1) |
(по свойствам логарифмов). |
|||||
Теперь дифференцируем обе части равенства по |
x: |
|||||
1 |
(lny)'x = [sinx·ln(x2 + 1)]'x, |
|
|
|||
y' = (sinx)'·ln(x |
2 |
+ 1) + sinx· (ln(x |
2 |
+ 1))', |
||
|
y |
|
|
|||
|
y' |
|
= cosx·ln(x2 + 1) + sinx· |
|
1 |
|
|
·2x, |
||||||||
|
y |
|
x2 +1 |
|||||||||||||
|
|
|
y' |
= cosx·ln(x |
2 |
+ 1) + |
|
2x sin x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||
Выражаем y′: |
|
y |
|
|
x2 +1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
2x sin x |
|
|
||||||
|
y' = y[cosx·ln(x |
|
+ 1) + |
|
|
|
|
|
], |
|
||||||
|
|
|
|
x2 +1 |
||||||||||||
|
|
|
2 |
|
sinx |
|
2 |
|
|
|
|
2x sin x |
||||
y' = (x |
|
+ 1) · (cosx·ln(x + 1) + |
|
|
|
|
|
. |
||||||||
|
|
x2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
||||
Пример 30. Найти производную степенно-показательной
функции
y = (x + 2)arcsin2x .
22
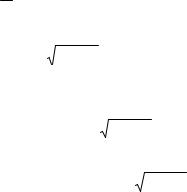
Решение.
Прологарифмируем данное равенство: lny = ln(x + 2)arcsin2x
lny = arcsin2x·ln(x + 2).
Дифференцируем последнее равенство по x: (lny)'x = (arcsin2x·ln(x + 2))'x,
yy' = (arcsin2x)'·ln(x + 2) + arcsin2x· (ln(x + 2))',
|
y' |
= |
|
1 |
|
|
2 ln(x +2) +arcsin 2x |
|
1 |
. |
|||||||||||
|
y |
|
−4x |
2 |
|
x +2 |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выражаем y′: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2ln(x +2) |
|
|
arcsin 2x |
|
|
|
|
|||||||||
|
|
|
y'= y |
|
|
|
|
+ |
|
|
|
|
|
|
, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x +2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
1−4x |
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2ln(x |
+2) |
|
arcsin 2x |
|
|||||||||
|
y'= (x +2)arcsin 2x |
|
|
|
|
|
|
+ |
|
|
|
|
|
. |
|
||||||
|
|
|
|
|
|
|
|
x +2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1−4x |
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.11. Задачи на нахождение касательной и нормали к кривой
Уравнение касательной к кривой y |
= f(x) в точке |
|||
Mo(x0, y0), лежащей на кривой, имеет вид: |
|
|||
y – y0 |
= kкас.(x – x0), |
(1) |
||
где y0 = f(x0), угловой коэффициент касательной |
kкас. = f '(x0). |
|||
Уравнение нормали в этой же точке имеет вид: |
|
|||
y – y0 |
= kнорм. (x – x0), |
(2) |
||
где y0 = f (x0 ), угловой коэффициент нормали |
|
|||
kнорм. = − |
1 |
|
(при f '(x0) ≠ 0). |
|
f '(x0 ) |
|
|||
|
|
|
||
Пример 31.Составить уравнения касательной и нормали к кривой y = x3 – 2x2 + 3 в точке с абсциссой x0 = 2.
Решение.
Вычислим значение y0 = f(x0) = 23 – 2·22 + 3 = 3.
Найдем производную функции и вычислим ее значение в точке x0=2:
23
y' = 3x2 – 4x,
kкас. = f '(x0) = 3·22 – 4·2 = 4.
Найденные значения подставим в уравнение (1) и получим урав-
нение касательной: |
|
|
|
|
|
y – 3 = 4(x – 2), |
|
|
|
|
|
y = 4x – 5. |
1 |
|
1 |
|
|
Найдём угловой коэффициент нормали: kнорм. = − |
= − |
. |
|||
kкас. |
4 |
||||
|
|
|
Запишем уравнение нормали, подставив найденные значения в уравнение (2):
y – 3 = − 14 ( x – 2), x + 4y – 14 = 0.
Пример 32. Составить уравнения касательной и нормали к кривой y = 
x +5 в точке с абсциссой x0 = 4.
Решение .Найдём y0 = f(x0) = 
4 +5 = 3.
Производная функции имеет вид:
y' = |
|
|
1 |
|
|
. |
|
|
|
|
|||
2 |
|
|
x +5 |
|
|
|
|
||||||
Вычислим угловой коэффициент касательной: |
|||||||||||||
kкас. = f '(x0) = |
|
|
|
1 |
|
|
= |
1 |
. |
||||
2 |
4 +5 |
|
|
||||||||||
|
|
|
|
|
6 |
|
|||||||
Составим уравнение касательной по формуле |
|||||||||||||
y – y0 = kкас. (x – x0): |
|||||||||||||
y – 3 = |
1 |
|
(x – 4), или |
||||||||||
|
|||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
||
x – 6y + 14 = 0. |
|
|
|
||||||||||
Найдём угловой коэффициент нормали: |
|
|
|
||||||||||
kнорм. = − |
1 |
|
= - 6. |
|
|
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
kкас. |
y – y0 = kнорм.(x – x0): |
|||||||
Запишем уравнение нормали по формуле |
|||||||||||||
y – 3 = - 6(x - 4), или 6x + y – 27 = 0.
24
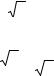
Уравнение касательной к кривой, заданной параметрическими уравнениями
x =ϕ(t), |
(9) |
|
y =ψ(t), |
||
|
||
при t = t0 имеет вид (1), если подставить в него |
|
x0 = ϕ(t0 ), y0 =ψ(t0 ), kкас. = y'x (t0 ).
Уравнение нормали имеет вид (2), если подставить в него
x0 = ϕ(t0 ), y0 =ψ(t0 ) , |
угловой коэффициент нормали |
|||||||||||||||||||||||
kнорм. = − |
|
1 |
|
= − |
|
|
1 |
|
|
|
(при y'x(t0) ≠ 0). |
|||||||||||||
|
|
|
|
|
y'x (t0 ) |
|
|
|||||||||||||||||
|
kкас. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 33. Составить уравнения касательной и нормали |
||||||||||||||||||||||||
к кривой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 3cost, |
|
|
|
|
|
при t0 = |
π |
. |
||||||||||||||||
|
= 2sin t, |
|
|
|
|
|
4 |
|||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Заметим, что это параметрические уравнения эллипса. |
||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдём координаты точки касания: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x0 = ϕ (t0) = 3cos |
π |
= |
|
3 |
2 |
|
, |
|
|
|
||||||||||||||
4 |
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y 0 = ψ (t 0 ) = 2sin |
π |
= |
2 |
2 |
|
= 2. |
||||||||||||||||||
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
Найдём производную по формуле |
(6): |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y'x |
= |
|
y't |
= |
(2sin t)' |
= |
|
2cost |
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x't |
(3cost)' |
|
−3sin t |
|
||||||||||||||||
Вычислим угловой коэффициент касательной: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|||
kкас. = y'x(t0) = |
|
2cos 4 |
= − |
|
2 |
. |
|
|||||||||||||||||
|
|
|
3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
−3sin |
π |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||
Составим уравнение касательной по формуле
25
|
|
|
|
y – y 0 |
= k кас. (x – x 0 ): |
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y - 2 = − |
|
х − |
|
|
|
или |
||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2x + 3y - 6 |
|
2 = 0. |
|
||||||||||
Найдём угловой коэффициент нормали: |
|
|||||||||||||||||
|
|
|
|
|
kнорм. = − |
|
1 |
|
= |
|
3 |
. |
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
kкас. |
|
|
||||||
Составим уравнение нормали по формуле |
|
|||||||||||||||||
|
|
|
|
y – y 0 |
= k норм. (x – x 0 ): |
|||||||||||||
|
|
3 |
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y - |
2 = |
|
|
х− |
|
|
, или |
|
|
|
6x – 4y - 5 2 = 0. |
|||||||
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В том случае, когда уравнение кривой задается в виде функции, заданной неявно, угловой коэффициент касательной найдём, подставив в выражение производной координаты точки касания M 0 (x0 , y0 ) :
kкас. = y′(x0 , y0 ).
Пример 34. Составить уравнение касательной и нормали к окружности:
(x – 1)2 + (y + 2)2 = 25
в точке M 0 (−2,2).
Решение.
Продифференцируем равенство по x:
((x – 1) 2 + (y + 2) 2 )' x = 0, 2(x – 1) + 2(y + 2) ·y' = 0.
Выразим y':
(y + 2) ·y' = 1 – x ;
26