Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный горный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

22.pdf

Скачиваний:

Добавлен:

06.06.2015

Размер:

1.26 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1513 14 15 > Следующая >>>

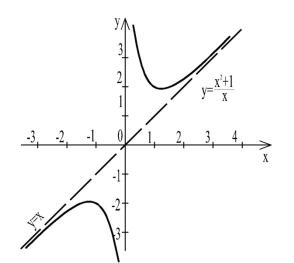
b= lim ( f (x) −kx) = lim (		x2 +1	− x) = lim	x2 +1− x2	= lim	1	= 0.
		x		x
x→∞	x→∞		x→∞		x→∞ x
Следовательно, прямая		y=x – наклонная асимптота (рис. 38).

Рис. 38

4.6. Общая схема исследования функции и построения графика

Исследование функции целесообразно вести в определенной последовательности.

1.Найти область определения функции, точки разрыва.

2.Найти вертикальные асимптоты.

3.Найти точки пересечения графика с осями координат, интервалы знакопостоянства функции.

4.Исследовать функцию на четность или нечетность, найти симметрию графика.

5.Найти наклонные асимптоты графика.

6.Найти точки экстремума, интервалы монотонности функции.

7.Найти интервалы выпуклости и точки перегиба графика функции.

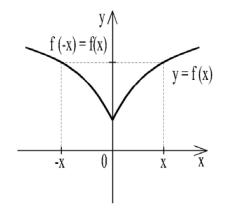
Определение. Функция f(x), определенная в области, симметричной относительно начала координат, называется четной, если f(-x)=f(x). График четной функции симметричен относительно оси ОY. Это значит, что та часть графика, которая соответствует отрицательным значениям х, получается зеркальным отражением относительно оси ОY той части графика, которая соответствует положительным значениям x (рис.39).

	Рис. 39
Например, функция f(x)=x2 – четная, так как		f(-x)=
=(-x)2=x2=f(x). Функция	f(x)=cos x – четная, так как	f(-x)=
=cos (-x)=cos(x)=f(x).
Определение.	Функция f(x), определенная в области,

симметричной относительно начала координат, называется не-

четной, если f(-x)=-f(x).

График нечетной функции симметричен относительно начала координат. Это значит, что если какая-либо точка принадлежит графику, то ему принадлежит также точка, симметричная относительно начала координат. Две точки называются симметричными относительно начала координат, если начало координат является серединой отрезка, соединяющего эти две точки

(рис.40).

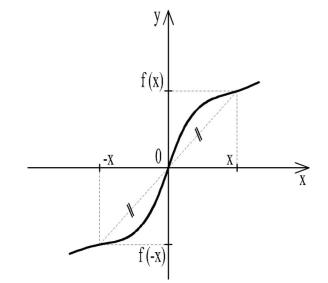
Рис. 40

Например, f(x)=x3 – нечетная, так как f(-x)=(-x)3=-=-x3=-f(x). Функция f(x)=sin x – нечетная, так как f(-x)= sin (-x)= -sin x=-f(x).

Функция y =	x2 +1	- нечетная, так как	f (−x) =	(−x)2 +1	= −	x2 +1	= − f (x) .

	x			− x		x

График этой функции симметричен относительно начала координат (см. рис. 38).

Пример 12. Исследовать функцию y =	x	и построить
	+ x2
1

ее график.

Решение.

1.Знаменатель 1+x2≠ 0, поэтому область определения функции – интервал (-∞,+∞). Точек разрыва нет.

2.Вертикальных асимптот нет (т.к. нет точек разрыва).

3. Если x=0,	то y =			0		= 0 . График пересекает ось OY в
		1		+02
точке О(0,0). Если	y =		х		= 0 , то x=0. График пересекает ось
точке О(0,0). Если	y =	+ x2			= 0 , то x=0. График пересекает ось
	1	+ x2
62

OX в точке О(0,0). Функция y =		х	> 0 при x>0, следовательно,
1		+ x2

график функции расположен выше оси Ox при x>0. Функция

y =

< 0 при

x<0, следовательно , график функции распо-

1+ x2

ложен ниже оси OX при x<0.

f (−x) =

− x

= −

= − f (x) ,

поэтому функция не-

1+(−x)2

1+ x2

четная, график симметричен относительно начала координат.

Ищем наклонную асимптоту y=kx+b

.Имеем:

k = lim

f (x)

= lim

= 0 ,

x→∞

x→∞ (1+ x2 )x

x→∞1+ x2

b = lim ( f (x) −kx) = lim

= lim

= 0.

+ x2

x→∞

x→∞1

x→∞ 1

x→∞

Следовательно, прямая y=0 – горизонтальная асимптота.

6. Находим производную

′

2 ′

)

1(1+ x )− x

y′=

(1+ x2 )2

1+ x2

1− x2

− x)(1

+ x)

(1+ x2 )2

y′ = 0

при x1=1,

Находим критические точки. Производная

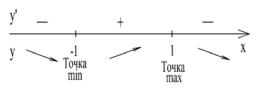
x2=-1. Критические точки разбивают ось OX на три интервала

(-∞,-1),

(-1,1), (1, +∞). Отметим на рис. 41 знаки произ-

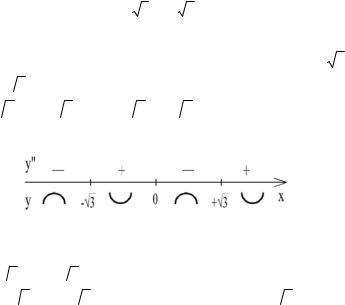
водной на каждом интервале.

Рис. 41

Следовательно, x1=1 – точка максимума,

f (1) =

+12

x2=-1

Критическая

−1

точка

–

точка

минимума,

f (−1) =

= −

Функция

возрастает на

интервале

+(−1)2

(-1,1), убывает на интервалах (-∞,-1), (1,+∞).

7. Находим вторую производную

′

(1− x

)(1+ x

) −

(1− x

+ x

)

1− x

) (1

y′′ =

(1+ x2 )

−

2x(1+ x2 )2 −

(1− x2 )2(1+ x

2 )2x

(1+ x2 )4

+ x2 )[−2x(1+ x2 )−4x(1− x2 )]

−2x −2x3 −4x + 4x3

(1+ x2 )4

(1+ x2 )3

2x(x − 3)(x +

2x3 −6x

2x(x2 −3)

(1+ x2 )3

Вторая

производная

равна

нулю

при

x1 = −

3 ,

x2 = 0, x3 = 3. Эти точки разбивают ось ОX на четыре интерва-

ла (-∞, − 3 ) , ( − 3 ,0) , (0, 3 ) , ( 3 , ∞). Отметим на рис. 42

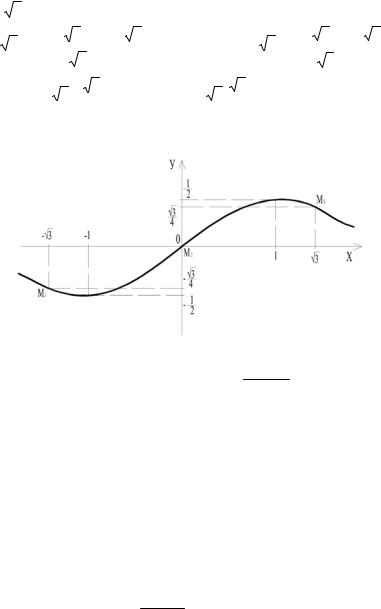
знаки второй производной на каждом интервале.

Рис. 42

Следовательно, график функции выпуклый вверх на интервалах (−∞,− 3) и (0, 3 ). График функции выпуклый вниз на интервалах (− 3,0) и ( 3,+∞). Таким образом, x1 = − 3 , x2 = 0 ,

x3 = 3			-	абсциссы						точек			перегиба.					Найдём		ординаты
f (− 3)=		− 3				= −				3		,	f (0)= 0 ,				f ( 3)=			3	=	3	.
f (− 3)=						= −						,	f (0)= 0 ,				f ( 3)=		(	3)2	=		.
	1+(− 3)2								4									1+	(	3)2		4
					3			M			(0,0), M					3
Точки M			−	3,−	3		,			2				3	3,	3		- точки перегиба.
Точки M			−	3,−			,								3,			- точки перегиба.
	1			4												4
				4												4

Пользуясь данными исследования, строим график функции

(рис. 43).

Рис. 43

Пример 13. Исследовать функцию y = (xx−−21)2 и построить её

график.

Решение.

1. Функция определена, если знаменатель x −1 ≠ 0 , x ≠1 . Таким образом, область определения – объединение интервалов (−∞,1) (1,+∞). Точка x =1 - точка разрыва функции.


2.	Так	как lim		(x −2)2		= +∞,	lim	(x −2)2	= −∞,
				x −1
		x→1+0					x→1−0 x −1
прямая х=1 – вертикальная асимптота графика функции.
3.	Если	x = 0 , то y =	(0 −2)2		= −4	. График пересекает ось ОY
			0 −1

в точке A(0,−4). Если y = (xx−−21)2 =0 , то x = 2 . График пересека-

4. f (− x)= (− x −2)2 − x −1

ет ось OX в точке	B(2,0). Функция		y =	(x −2)2	>0 , при	x >1 ,

				x −1
следовательно, график функции расположен выше оси OX при
x >1 . Функция y =	(x −2)2	< 0 при	x < 1 , следовательно, график

	x −1

функции расположен ниже оси OX при x < 1 .

≠ f (x), f (−x)≠ −f (x), поэтому функ-

ция общего вида (не является ни чётной, ни нечётной). 5. Ищем наклонную асимптоту y = kx +b . Имеем:

k = lim

f (x)

= lim

(x −2)2

= lim

−4x +4

− x

x→∞

→∞ x(x −1)

x→∞

−

= lim

=1,

x→∞

−

1−

−2)2

−2)

2 − x(x −1)

b = lim ( f (x)

−kx) = lim

−1 x

= lim

x→∞

x −1

x→∞

x −1

x→∞

x2 −4x +4 − x2 + x

−3x +4 = lim

−3x

= lim

x→∞

x −1

→∞

x −1

x→∞

−

−3 +

= lim

= −3.

x→∞ 1−

Прямая y = x −3 - наклонная асимптота графика функции. 6. Находим производную

(x −2)

′

((x −2)

)(x −1)−(x −2) (x −1)

y′ =

x −1

(x −1)

2(x −2)(x −1)−(x −2)2

(x −2)(2(x −1)−(x −2))

(x −1)2

(x −2)(2x −2 − x + 2)

(x −2)x

(x −1)2

Находим

критические

точки. Производная

′

y =0 при

x1 = 2, x2 =0.

Производная

не существует при x3 =1. Критиче-

ские

точки

разбивают

ось Ox на

четыре

интервала

(−∞,0),(0,1),(1,2),(2,+∞)

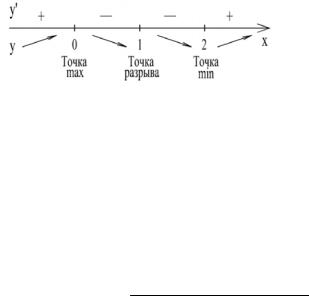
. Отметим на рис. 44

знаки производной

на каждом интервале.

Рис. 44

Следовательно,

x1 = 2 -

точка минимума, f (2)= 0 . Критиче-

ская точка

=0 – точка максимума, f (0) = −4 . Критическая

точка x3

точка разрыва. Функция возрастает на интервалах

(−∞,0) и

(2,+∞). Функция убывает на интервалах (0,1) и (1,2).

Находим вторую производную

(x − 2)x ′

−2x ′

(x2 −2x)′(x −1)2 −(x2 − 2x)((x −1)2 )′

′′

(x −1)

−1)

(x −1)

(2x −2)(x −1)2 −(x2 −2x)2(x −1)

(x −1)([2x −2)(x −1)−

(x2 − 2x)2]=

(x −1)4

2x2

−2x −2x + 2 − 2x2 + 4x

(x −1)3

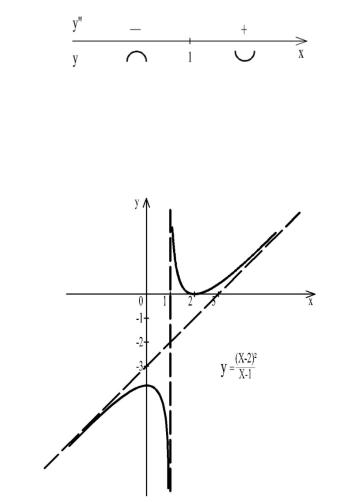
Вторая производная не существует при x =1 . Эта точка разбивает ось ОХ на два интервала (−∞,1) и (1,+∞). Отметим на рисунке 45 знаки второй производной на каждом интервале.

Рис. 45

Следовательно, график функции выпуклый вверх на интервале (−∞,1), выпуклый вниз на интервале (1,+∞). Точка x =1 - точ-

ка разрыва функции, поэтому точек перегиба нет. График исследуемой функции изображён на рис. 46.

Рис. 46

Пример 14. Исследовать функцию y =	4x +4	и построить
	(x +2)2

её график.

Решение.

1. Функция определена, если знаменатель (x + 2)2 ≠ 0 , x ≠ −2 . Таким образом, область определения функции – объединение интервалов (−∞,−2)U(−2,+∞). Точка x = −2 - точка разрыва.

Так как

lim

4x +4

= −∞, прямая x = −2

- вертикаль-

x→−2±0 (x +2)2

ная асимптота.

0 +4

Если x = 0 , то y =

=1. График пересекает ось OY в

(0 +2)2

точке

A(0,1).

Если y =

4x +4

=0 ,

то 4x + 4 = 0, x = −1.

График

(x +2)2

пересекает ось ОХ в точке B(−1,0).

4(x +1)

Функция

y =

>0 при

x > −1,

следовательно,

график

(x +2)2

функции расположен выше

оси

ОХ

при

x > −1.

Функция

4(x +1)

y =

при

x < −1,

следовательно,

график

функции

(x +2)2

расположен ниже оси ОХ при

x < −1.

f (− x)=

−4х+4

≠ f (x)

f (−x)≠−f (x),

поэтому функция

(− x +2)2

общего вида.

Ищем наклонную асимптоту y = kx +b . Имеем

k = lim

f (x)

= lim

4x +4

= lim

4x +4

x→∞

x→∞ x(x +2)2

x→∞ x3 +4x +4x

= lim

= = lim

=0,

4x2

4 4

x→∞

b = lim (f (x)−kx)= lim

4x +4

= lim

4x +4

(x +2)2

x→∞

x→∞ x2 +4x +4

= lim

= 0.

4 4

x→∞ x2

x→∞

Прямая y = 0 - ось ОХ - горизонтальная асимптота графика

функции.

6. Находим производную

4(x +1)

′

(x +1) (x + 2)

−(x +1)(x + 2)

)

y′ =

= 4

(x +

(x +2)

= 4

(x +2)2 −(x +1)2(x +2)

= 4

(x +2)((x +2)−2(x +1))

(x +2)4

(x + 2)4

= 4

x +2 −2x −2

= −

(x +2)3

(x +2)3.

Находим критические точки.

′

Производная y =0 при x1 =0 .

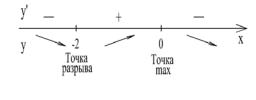
Производная не существует при x2 = −2 . Критические точки разбивают ось ОХ на три интервала (−∞,−2), (−2,0), (0,+∞). Отметим на рисунке 47 знаки производной на каждом интервале.

Рис. 47

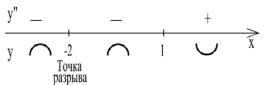
Следовательно, функция возрастает на

интервале (−2,0),

убывает на интервалах

(−∞,−2) и

(0,+∞).

Точка x1 =0 - точка

максимума,

f (0)=1. Точка x2 = −2

– точка разрыва.

Находим

вторую

производную:

′

3 ′

y′′ =

−

= −4

x (x + 2) − x((x + 2) )

+ 2)

(x + 2)

= −4

(x + 2)3 − x 3(x +2)2

= −4

(x +2)2 (x +2 −3x)

(x +2)6

= −4

2 −2x

8(x −1)

(x + 2)4

(x +2)4

Вторая производная

y′′ = 0 при x1 =1,

не существует при

x2 = −2 . Эти точки разбивают ось ОХ на три интервала. Отметим на рисунке 48 знаки второй производной на каждом интервале.

Рис. 48

Следовательно, график функции выпуклый вверх на интервалах (−∞,−2) и (−2,1), выпуклый вниз на интервале (1,+∞), x =1 - абсцисса точки перегиба. Найдем ординату точки перегиба

f (1)=	4	1+4		8			8
			=		. Точка	M 1,		- точка перегиба.
	(1+2)2		=	9	. Точка	M 1,	9	- точка перегиба.
	(1+2)2			9			9

Пользуясь данными исследования, строим график функции

(рис.49).

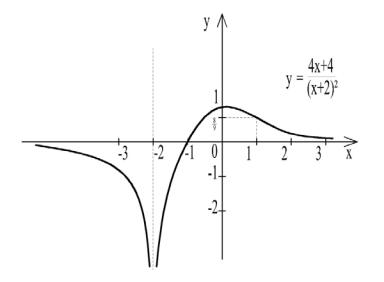
Рис. 49

ПРИЛОЖЕНИЕ Дифференцирование обратной функции


Теорема. Пусть функция	y = f (x)		возрастает (или убывает)
в некоторой окрестности точки		x0	и имеет непрерывную об-
ратную функцию x = g( y).	Если в точке x0 функция y = f (x)

имеет производную			y′x = f ′(x0 ) ≠ 0,			то обратная функция имеет
производную в соответствующей точке								y0 = f (x0 ), причем
′	′	1		или	′	1	.	(16)

xy = g ( y0 ) =		f ′(x0 )			xy =	y′x

Доказательство. Придадим аргументу обратной функции x = g( y) в точке y0 приращение y ≠ 0. Тогда обратная функ-

ция получит приращение x ≠ 0 благодаря своей монотонности. Поэтому можно написать следующее тождество:

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1513 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.04.2019516.61 Кб42012 индивидуальное задание (экономика природоп....doc
#
16.04.2019250.37 Кб32012 КОНСПЕКТ ДО САМОС РОБІТ подтки.doc
#
29.09.201996.63 Кб1520121230_pr_2287_1.docx
#
19.12.201837.92 Кб521.docx
#
08.09.201975.26 Кб422-30.doc
#
06.06.20151.26 Mб3622.pdf
#
19.12.201841.05 Кб223.docx
#
19.12.20181.29 Mб3224.docx
#
07.07.20196.08 Mб20251185.rtf
#
01.08.2019146.94 Кб225_26_27_28_29_30_31.doc
#
18.11.20192.18 Mб1026.09.07 практикум соціологія.doc