kvant_mech

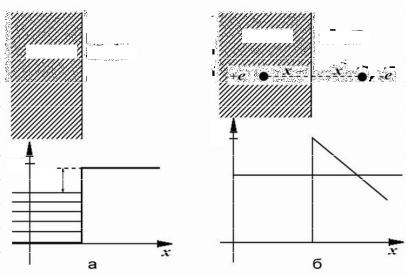
массы частицы, ширины барьера и его высоты над Е. Поэтому туннельный эффект не играет никакой роли в макроскопических явлениях. Например, для массы 10–4г, при дефиците энергии 10–8 эрг и ширине барьера 10–4 см, показатель экспоненты

равен 3·1017 и прозрачность барьера D~e−31017~10−17 !

Однако для частиц микромира он может иметь очень большое значение, например, в ядерной физике. Здесь мы рассмотрим один пример: явление холодной эмиссии.

§25 Холодная эмиссия

В электродинамике мы видели, что для электронов в куске металла поле можно представить в виде прямоугольной ямы. При включении внешнего поля, «вытягивающего» электроны напряженностью E, a добавка к потенциальной энергии электрона вне металла –eEx.

Металл Вакуум

Металл Вакуум

U U0

0 Aвых

Рис.15 а) в отсутствии внешнего поля, б) внешнее электрическое поле E

71

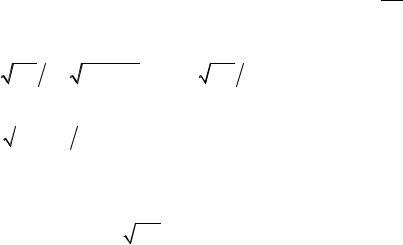
Таким образом, в области справа возникает потенциальный барьер,которыйдлясамыхбыстрыхэлектроновсэнергиейЕ=Еф в точке с координатой x имеет высоту ϕ(x)=–еЕx+U0–Еф или ϕ(x)= –еЕx+А, где А=U0–Еф –работа выхода электрона. Класси-

ческая точка поворота определяется из соотношения Тогда показатель в экспоненте равен:

Следовательно, для зависимости силы тока холодной эмиссии от напряженности поля получим I=I0e–C/E, где I0 сила тока

при E→ , а C = 4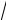2m A3/2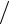3eħ , где A=U0–Еф – работа выхода электрона из металла. Ток нарастает плавно от E=0 и

становится ~ I0 при E~C (происходит “насыщение”). Сравним этот результат с предсказаниями классической

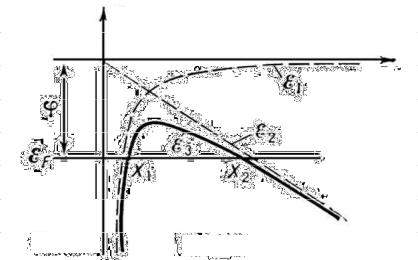
физики. На первый взгляд холодная эмиссия вообще невозможна, т.к. барьер имеет неизменную высоту при любых E, а туннельный эффект не существует. На самом деле это не так, поскольку на вылетевший электрон действует не только внешнее поле, но и сила его «изображения» е2/4х2, которая создает добавку к потенциалу –е2/4х, и полный потенциал снаружи будет U(x)= –e E х–е2/4х+U0–Еф.

72

U

x

Металл Вакуум

Рис. 16 Потенциальная энергия φ электрона вблизи поверхности металла

х—расстояниеотповерхности;Е1—вотсутствииэлектриче- ского поля; Е2 — в однородном внешнем электрическом поле; Е3 — суммарная потенциальная энергия электрона; Еф — энергия Ферми металла; x2 — x1 — ширина потенциального барьера в присутствии поля.

Максимум этой функции определяется из –e E +е2/4х02=0. Откуда х0=½(е/ E )½ и U(x0)= –e3/2 E 1/2+U0–Еф.Высота барьера понижается на e3/2 E 1/2. В классической модели холодная эмиссия начнется, когда потенциал сравняется с энергией электронов,находящихсянауровнеФерми,т.е.приe3/2E 1/2≥U0–Еф или приE0=(U0–Еф)2/е3=А2/е3.Графиктоканачинаетсясэтойточки и идет значительно ниже кривой, предсказываемой квантовой механикой. Опыт однозначно говорит здесь в пользу квантовой природы холодной эмиссии.

73

Математический аппарат квантовой механики

Операторы квантовой механики

ЛЕКЦИЯ 10

§26 Постулат средних значений. Линейность. Эрмитовость

Мы видели, что проекциям импульса в квантовой механике

ратор Uˆ =U . Обобщая эти результаты, мы введем следую-

щий постулат:

Каждой физической величине L в квантовой механике сопоставляется некоторый оператор Lˆ . Этот постулат по-

рождает вопросы:

1.Как его найти?

2.Какой смысл имеет термин «сопоставляется»?

3.Накладываются ли какие-либо ограничения на операторы,

сопоставляемые физическим величинам?

Ответы:

1. Если величина в классической механике является функцией координат и импульсов, то оператор Lˆ получается из соответствующих классических формул с помощью замены координат операторами умножения на эти координаты,

74

xˆ = x ; yˆ = y ; zˆ = z , а проекций импульса, соответствен-

но, на −i ∂∂x ; −i ∂∂y ; −i ∂∂z .

Пример:

В классической физике момент импульса частицы определяется формулой: l =[r × p], а его проекции формулами:

lx=ypz–zpy, ly=zpx–xpz, lz=xpy–ypx. В квантовой механике проекциям момента импульса сопоставляются операторы:

Если величина L в классической механике не фигурирует, для соответствующего оператора Lˆ приходится прибегать в каждом случае к специфическим рассуждениям.

2. На второй вопрос ответ дает постулат средних значений, согласно которому среднее значение физической величины L в состоянии с волновой функцией Ψ задается формулой:

L = ∫∫∫ψ*Lˆψ dV . Это соотношение для операторов Lˆ типа

умножениянакакую-либофункциюкоординатF(x,y,z)очевид- но:

F = ∫∫∫ψ *F(x,y,z)ψdV = ∫∫∫F(x,y,z)ψ *ψdV =

= ∫∫∫F(x,y,z)dw , что совпадает с определением среднего. Для других случаев мы примем это как постулат.

75

3.а. Операторы, сопоставляемые физическим вели-

Lˆ(c1ψ1 +c2ψ2) = c1Lˆψ1 +c2Lˆψ2. Можно проверить, что опе-

раторы pˆ , xˆ иихвещественныефункцииудовлетворяютусловию линейности.

3.б. Операторы квантовой механики, сопоставляемые физическим величинам, для широкого класса функций Ψ1 и Ψ2 должны удовлетворять условию:

∫∫∫ψ1* Lˆψ2dV = ∫∫∫ψ2(Lˆψ1)* dV ≡ ∫∫∫(Lˆψ1)*ψ2dV .

Это условие называется условием самосопряженности или «эрмитовости», оно позволяет «перебросить» действие оператора с функции Ψ2 на Ψ1 и гарантирует при Ψ1=Ψ2 веществен-

ность среднего значения L:

L = ∫∫∫ψ1* Lˆψ1dV = ∫∫∫ψ1(Lˆψ1)* dV = L* .

Эрмитовостьоператоров xˆ , yˆ , zˆ иихвещественныхфункций очевидна (простое умножение). Докажем эрмитовость

= ∫ψ2 −i ∂∂ψx1 *dx

Мы воспользовались интегрированием по частям и тем, что Ψ2 и Ψ1 должны обращаться в нуль при х→± . Заметим, что функции, соответствующие инфинитному движению, напри-

76

мер, exp{i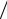 (pr − Et)}– плоская волна де Бройля, не удовлетворяют этому требованию, мы можем, однако, всегда считать, что частица находится в ящике очень больших размеров и волновая функция обращается на его стенках в нуль.

§27 Алгебра операторов. Коммутаторы. Обратный и единичный операторы. Функции оператора

1. Сумма и разность операторов определяются очевидны-

ми равенствами:

(Lˆ ± Mˆ )ψ = Lˆψ ± Mˆψ .

2.Произведение операторов LMˆ ˆ определяется как после-

довательное действие операторов Mˆ (сначала) и Lˆ (потом) на волновую функцию Ψ. В общем случае произведение операторов не подчиняется коммутативному закону и

LMˆ ˆ ≠ MLˆ ˆ .

3. Разность LMˆ ˆ − MLˆ ˆ называется коммутатором операторов Lˆ и Mˆ и обозначается [Lˆ,Mˆ ]. Вычислим, например,

коммутатор операторов xˆ и pˆx , и покажем, что они не коммутируют:

[xˆ,pˆx ]ψ ≡ (xpˆˆx − pˆx xˆ)ψ = −i x ∂∂ψx +i ∂∂x (xψ)=i ψ .

Откуда (xpˆˆx − pˆx xˆ) = i .

Оператор проекции импульса на какую-нибудь ось и оператор координаты вдоль другой оси, очевидно, коммутируют, и

77

(xˆi pˆxk − pˆxk xˆi ) = 0 при i≠k.

4. Докажем одно важное свойство эрмитовых операторов: Произведение эрмитовых операторов LMˆ ˆ есть также эрмитов оператор:

∫∫∫ψ1*LMˆ ˆψ2dV = ∫∫∫Mˆψ2(Lˆψ1)*dV = ∫∫∫(Lˆψ1)*Mˆψ2dV =

= ∫∫∫ψ2(MLˆ ˆψ1)* dV .

Откуда следует эрмитовость LMˆ ˆ . В частности, из этого сле-

дует эрмитовость операторов проекций момента импульса:

lˆx = ypˆ ˆz − zpˆˆ y .

5. Оператор Lˆ−1 называется обратным оператору Lˆ и определяется равенством: LLˆ ˆ−1 = Iˆ, где Iˆ – оператор тождественного преобразования такой, что Iˆψ =ψ .

Подействуем оператором Lˆ−1 на обе стороны определяющего равенства Lˆ−1Lˆ (Lˆ−1ψ)= Lˆ−1Iˆψ = Lˆ−1ψ = ILˆˆ−1ψ = LLˆ ˆ−1 (Lˆ−1ψ), от-

куда следует Lˆ−1Lˆ = LLˆ ˆ−1 = Iˆ .

Из сказанного следует, что для операторов Lˆ и Mˆ , если они не коммутируют друг с другом, существуют два частных

Lˆ−1Mˆ и MLˆ ˆ−1.

6. Для рациональной или разлагающейся в ряд функции

78

ЛЕКЦИЯ 11

§28 Собственные функции и собственные значения оператора

Рассмотрим физическую величину L и соответствующий ей оператор Lˆ . Найдем средний квадрат флуктуации (∆L = Lˆ − L) этой величины всостояниисволновойфункцией Ψ. Согласно определению среднего значения имеем:

∆L2 = ∫∫∫ψ* (Lˆ − L)2ψdV .

Пользуясь эрмитовостью оператора Lˆ − L, преобразуем это выражение:

∆L2 = ∫∫∫[(Lˆ − L)ψ]* (Lˆ − L)ψdV = ∫∫∫|(Lˆ − L)ψ |2 dV .

Поставим теперь себе целью найти такие состояния Ψ, в которых отсутствует разброс значений L и эта величина имеет определенное значение, совпадающее со средним значени-

ем: L = L и ∆L2 = 0. Поскольку подинтегральная функция не отрицательна, это возможно, если только эта функция тожде-

Таким образом, для того, чтобы в состоянии с волновой функцией Ψ величина L имела определенное значение, Ψ должна быть

решением этого уравнения. Иначе говоря, оператор Lˆ , действуя на Ψ, должен ее воспроизводить, но с численным коэффици-

79

ентом L, равным искомому значению величины L. Волновые функции, удовлетворяющие этому, называются собственными функциями,анаборчиселL –собственнымизначениямиопера-

тора Lˆ . Если Ψ не удовлетворяет (15.2), то в таком состоянии L не имеет определенного значения и существует разброс значений этой величины.

Проиллюстрируем это на примере частицы в ящике с непроницаемыми стенками. Мы видели, что для нее волновые

функции определяются формулой: ψn = a2 sin nπa x .

ональна Ψn, то последняя не является собственной функцией оператора pˆx , и проекция импульса не имеет определенного значения. Физически это очевидно, т.к. в силу симметрии за-

80