kvant_mech

поляризацияволнылинейнаяивектор Eω0 направленвдольоси Х,тосоставляющаясилы Fx = eEω0 cos(ωt −2πz /λ) = −∂∂Ux

и U (1) = −exEω0 cosωt , а значит Hˆ (1)(t) = −exEˆ ω0 cosωt .

Подсчитаем матричные элементы оператора Hˆ (1)(t). По определению:

Hmn(1)(t) = ∫ψm* Hˆ (1)ψndV = −eEω0 cosωt ×∫ψm* xˆψndV = = −exmn Eω0 cosωt ,

если ввести обозначение: exmn = e∫ψm* xψndV .

Чтобы уяснить смысл этого выражения рассмотрим случай

равных индексов n = m. Тогда exmm = e∫ψm* xψmdV = ex , т.е. эта величина есть средний дипольный момент атома в состоянии m в направлении х, если один из зарядов, например, ядро

поместить в начале координат. В формуле для Hmn(1) индексы смешанные, и мы можем интерпретировать это как средний «дипольный момент перехода» межу состояниями с номерами n и m. Совокупность величин xmn дает матрицу:

Таким образом, производные коэффициентов am(1)(t) могут быть представлены в виде:

161

dadtm(1) = − i (−exmn Eω0 cosωt)eiωmnt =

= 2i exmn Eω0[ei(ωmn +ω)t +ei(ωmn −ω)t ] .

Чтобы получить am(t) нужно проинтегрировать от 0 до t:

Квадратыэтихкоэффициентовописываютвероятностипереходов между уровнями с номерами n и m. Если Em>En, то переход n m происходит с поглощением энергии и ωmn>0; если Em<En, то переход n m происходит с излучением энергии и ωmn<0. Поскольку, как мы увидим, в физически содержательных случаях |ωmn| ω, в случае поглощения энергии первый член в квадратных скобках много меньше второго, в случае излучения – наоборот.

Рассмотрим случай излучения. Тогда квадрат величины am(t) определяет, очевидно, вероятность излучения кванта за время t:

Таким образом, вероятность перехода пропорциональна квадрату напряженности поля и квадрату дипольного момента перехода (поэтому оно и называется дипольным). Из формулы

162

видно, что вероятность для любого момента времени имеет острый пик при |ωmn| ω. Чтобы убедиться в этом, введем за-

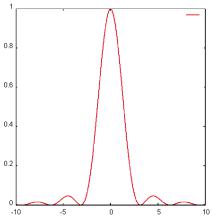
Исследуем поведение множителя f (ξ)= sin2 ξ .

ξ 2

(sin(x)**2)/x**2

f (ξ) =(2/5π)2=0,016 и т.д.

Максимум очень узкий, т.к. при ω~1015 и t 10-8 сек (время “жизни”) ξуже больше 107, а f (ξ)<10−14 !

163

Поэтому заметная вероятность перехода под действием вынуждающей силы имеет место в очень узком интервале частот вблизи ωmn, и атомные колебательные системы имеют очень высокую (~107) добротность. По своему смыслу вероятность должна быть пропорциональна времени, а не квадрату синуса! Для получения правильного результата нужно учесть еще немонохроматичность реальной волны и ширину (пусть малую!) спектральной линии. С этой целью проинтегрируем полученную формулу в пределах ширины спектральной линии по интервалу частот. Поскольку ширина очень узка, интегрировать можно в пределах от 0 до . Воспользуемся уже введенной заменой переменных и соотношением их дифференциалов

dω = 2dξ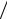t :

ность можно выразить и через плотность энергии электромаг-

Откуда wmn = 2π2e2 xmn 2 t ρω , где ρω – плотность энергии в

2

плоской электромагнитной волне на частоте ω.

164

Дипольное излучение и поглощение

Лекция 21

§59 Матрица дипольных переходов. Правила отбора их физический смысл.

«Разрешенные» и «запрещенные» переходы. Характер поляризации излучения

Итак, вероятность перехода связана с матричным элементом матрицы дипольного момента. Например, для радиальной сим-

метрии: erjk = e∫ψ*j rˆψk dV . Для многих состояний эти элементы оказываются равными нулю. Рассмотрим уже известные

системы.

∞

а). Гармонический осциллятор. xmn = ∫ψm* xψndx .

−∞

Полученные нами ранее волновые функции име-

165

только при условии, что m=n+1 или m=n–1, значит, возможны переходы только при n n 1, т.е. n= 1, откуда

ωmn = Em − En = ∆n ω0 =ω0 . Поэтому в линейном осцилляторе возможны переходы только между соседними уровнями

xjk = ∫ψ*j xψk dV , yjk = ∫ψ*j yψk dV , z jk = ∫ψ*j zψk dV .

Общий вид собственных функций оператора момента ко-

y = sinϕsinθ, z = cosθ, dV = sinθdθdϕ.

Пусть в состоянии j и k квантовые числа имеют значения l’, m’ и l, m, соответственно. Тогда, подставляя функции в интегралы, имеем:

166

Последний интеграл по φ не равен нулю только при m=m’, откуда ∆m=0. Первые два не равны нулю только при ∆m= 1.

xjk = yjk = 0,

т.е. при таких переходах колебания происходят «вдоль z” и возникающая волна поляризована линейно.

Для∆m= 1матричныйэлементz jk =0,а xjk и yjk «сдвинуты по фазе» на π/2 (из-за множителя 1/i), возникающая волна поляризована по кругу. Для рассмотрения второго интеграла ограничимся матрицей z jk , не равной нулю при m=m’, которую можно записать в виде:

z jk = 2ππ∫Plm (cosθ) Pl 'm (cosθ)sinθ cosθdθ .

так называемые, шаровые функции, для которых в математике доказана рекуррентная формула:

ηPlm (η) = 2l l++m1Pl−1,m (η)+ l −2lm++11Pl+1,m (η).

Опять в силу ортогональности:

только при l’=l 1, т.е. l= 1.

Все, что мы получили для момента количества движения верно и для атома водорода и водородоподобных ио-

167

нов, но нужно еще учесть радиальную функцию, поскольку

ψnlm = Rnl (r)Plm (θ)eimϕ и dV = r2 sinθdθdϕdr . к рассмо-

тренным уже интегралам добавится множитель вида:

∞∫Rn'l ' (r) rRnl (r)r2dr .

0

Таким образом, для l и m правила отбора сохранятся, а при их выполнении последний интеграл не обращается в нуль при любых n и n’. Следовательно, все переходы по n разрешены.

168

ЛЕКЦИЯ 22

§60 Эмпирические законы теплового излучения. Закон Вина. Формула Релея-Джинса. «Ультрафиолетовая катастрофа». Формула Планка для плотности излучения в термодинамическом равновесии

Одной из проблем, которая не подавалась решению в рамках классической физики в «допланковское» время, была проблема излучения нагретых тел, или теплового излучения (не инфракрасного, а излучения, возбуждаемого тепловым движением атомов). Еще в XIX-м веке экспериментально были установлены внешние закономерности этого явления. Распределение интенсивности излучения по частотам (длинам волн) имело вид характерной кривой с максимумом, с убыванием как в сторону малых, так и в сторону больших длин волн или частот. Высота максимума пропорциональна пятой степени абсолютной температуры, а его положение на шкале длин волн определяется

формулой: λ(max) = C /T (закон смещения Вина). Было установлено, что полная энергия, излучаемая единицей поверхно-

сти нагретого тела за секунду на всех длинах волн пропорциональна четвертой степени абсолютной температуры u =σT 4 (закон Стефана-Больцмана).

Чтобы рассмотреть равновесие тела с окружающим его излучением, введем понятие поглощательной и излучательной способности тела. Первая показывает, какая доля (Aν) падающей в интервале частот ν, ν+Δν энергии остается внутри тела, превращаясь в тепло. Тело у которого Aν=const стали называть «серым», а если Aν=1, – «абсолютно черным» или просто «черным».Вэкспериментахчерноетелообычномоделируютзачер-

169

ненной полостью, часто сферической, с малым отверстием, в которое свет попадает почти по касательной к поверхности и полностью поглощается при многократных отражениях. Излучательная способность (Eν) – энергия излучаемая 1 см2 нагретого тела за секунду в том же интервале частот.

Еще в середине XIX столетия Кирхгофом с использованием второго закона термодинамики было показано, что при равновесии рассматриваемого тела с окружающим его излучением выполняется соотношение:

Eν = 8cπ ρν ,

Aν

где ρν – спектральная плотность излучения в объеме. Это указывает, что рассматриваемое отношение не зависит от тела и спектральная плотность излучения, находящегося в равновесии с телом, есть универсальная функция температуры, т.е.:

ρ(ν)dν = F(ν,T )dν .

Виномбылополучено,чтоформула,удовлетворяющаязаконам термодинамики должна иметь вид (функция Вина):

ρ(ν)dν =ν3F ν dν .

T

Эта формула оказалась очень полезной, т.к. подтвердила, по крайней мере, две экспериментальные закономерности. ИнтегрированиеэтойформулыповсемчастотамдаетзаконСтефана Больцмана:

170