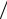kvant_mech

где ξ =νT . (напомним, что определенный интеграл это – чис-

ло).

Приравнивая нулю производную функции Вина, можно получить:

Если решить это уравнение относительно аргумента функции, мы получим частоту, отвечающую максимуму излучательной

способности тела ν(max)T = bν или λ(max)T = bλ – закон смеще-

ния Вина.

Но вид функции F(v/T) оставался неопределенным. Рассматривая систему стоячих волн электромагнитного из-

лучения в замкнутой полости, Релей и Джинс в конце XIX века нашли формулу,

которая удовлетворяет закону Вина. Более того, она хорошо описывает экспериментальные данные в области низких частот, но приводит к абсурду при вычислении полной энергии, излучаемой единицей поверхности за единицу времени:

Этот «феномен» был назван «ультрафиолетовой катастрофой».

171

Поскольку при низких частотах формула Релея-Джинса давала хорошие результаты, начались поиски безразмерной «обрезающей» функции с аргументом вида (ν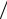T ), которая бы эту «катастрофу преодолела. Эти поиски привели в 1900-м году Макса Планка к его знаменитой формуле, удовлетворяющей закону Вина:

ρν dν = 8πνc33 ehν kT1 −1dν ,

которая сначала была получена эмпирически. При анализе этой формулы пришлось сделать предположение, противоречившее всему духу классической физики, что гармонические осцилляторы излучают энергию дискретно, порциями – квантами ε0=hν. Так было положено начало квантовым представлениям в физике.

172

Спонтанное и вынужденное излучение

ЛЕКЦИЯ 23

§61 Вывод формулы Планка по Эйнштейну

Мы получим формулу Планка, используя вывод, аналогичныйпримененномуЭйнштейном,болеестрогийинеограничивающийся случаем гармонического осциллятора.

Пусть En и Em (<En) два уровня энергии атома или иной квантовой системы. Число спонтанных переходов за единицу времени равно вероятности спонтанного перехода Anm , умноженной на число возбужденных атомов.

wnmc = Anm Nn .

Число вынужденных переходов с излучением равно вероятности перехода Bnm , умноженной на число возбужденных атомов и плотность энергии электромагнитного поля на соответствующей частоте: wвnm=BnmNn ρ(v,T ), а число вынужденных переходов с поглощением равно вероятности перехода Bnm , умноженной на число не возбужденных атомов и плотность энергии электромагнитного поля: wПnm=BnmNn ρ(v,T ). Вероятности Anm , Bmn , Bnm получили название «коэффициенты Эйнштейна». В равновесии число переходов «вверх» и

«вниз» равны. Следовательно,

wсnm+wвnm =wПnm и Anm Nn =[Bmn Nm − Bnm Nm ]ρ(ν,T ).

173

Смысл этого предельного соотношения в том, что при одинаковой «заселенности» вероятности поглощения и излучения под действием поля, в соответствии с теорией возмущения, должны быть одинаковы. Следовательно,

ρ(ν,T ) = Anm /Bnm . ehνkT −1

На низких частотах:

ehνkT −1= hν kT , и ρ(ν,T ) = AnmkT .

Bnmhν

Но должна быть справедлива формула Релея-Джинса:

ρ(ν,T ) = 8πν3 2 kT = Anm kT ,

c Bnmhν

откуда Anm = 8πhν3 .Окончательно,получаемформулуПлан-

Bnm c3

174

ка: ρ(ν,T ) = 8πch3ν3 ehν kT1 −1.

В качестве упражнения студентам предлагается получить из этой формулы законы Стефана-Больцмана и Вина, вводя в качестве безразмерной переменной ξ=hv/kT.

175

Квантовая теория молекулярной связи

ЛЕКЦИЯ 24

§64 Спиновые волновые функции системы двух электронов.

Симметричные и антисимметричные функции. Синглетные и триплетные состояния

В теории химической связи фундаментальное значение имеет спин электрона. Обычно химическая связь образуется при образовании пар электронов, принадлежащих атомам, вступающимвтакуюсвязь.Поэтомудлядальнейшегонамнужнорассмотреть спин системы двух электронов. Операторы спина для одного электрона вводятся в матричной форме и имеют вид:

иобщие собственные функции коммутирующих операторов Sˆ2

иSˆz

176

оператора Sˆz равным ħ/2 и –ħ/2 для α1 и α2, соответственно,

Перейдем теперь к системе двух спинов. Построим операторы, считая, что спины не взаимодействуют между собой. Операторы полного спина и z-проекции будут иметь вид:

Sˆ2 = (Sˆ1 + Sˆ2)2 = Sˆ12 + Sˆ22 + 2(Sˆ1x Sˆ2x + Sˆ1y Sˆ2y + Sˆ1z Sˆ2z ), Sˆz = Sˆ1z + Sˆ2z .

Введем, также, спиновые волновые функции двух электронов: α1(1), α1(2), α2(1) и α2(2), аргументы показывают, какому из двух электронов принадлежат эти функции. Операторы спина действуют только на «собственные» функции. Поскольку

177

мы пренебрегли взаимодействием спинов, спиновые функции должны представлять собой произведения односпиновых функций αi(1) и αi(2) и, согласно сказанному ранее, эти произведения должны быть симметризованы или антисимметризованы. Легко видеть, что можно составить три симметричные функции:α1(1)α1(2),α2(1)α2(2),α1(1)α2(2)+α1(2)α2(1)иодну антисимметричную: α1(1)α2(2)–α1(2)α2(1). Три первые не меняют знака при перестановке номеров электронов, а последняя

– меняет знак.

Покажем, что эти функции являются собственными для опе-

раторов Sˆ2 и Sˆz и найдем их собственные значения.

= 2 2α1(1)α1(2).

Аналогичный результат можно получить для двух других симметричных комбинаций. Таким образом, все симметричные волновые функции являются собственными функциями опера-

тора Sˆ2 , принадлежащими собственному значению оператора Sˆ2 =ħ2S(S+1)=2ħ2 и квантовому числу S=1.

Обратимся теперь к Sˆz .

178

Таким образом, три симметричные функции являются соб-

ственными функциями оператора Sˆz , соответствующими зна-

чениям квантового числа MS, равным 1, 0, –1 и Sz =ħ, 0, –ħ, о таких состояниях условно говорят, что спины у них «параллельны» и называют их триплетными.

Антисимметричная комбинация соответствует MS=0 и Sz=0.

Вычислим, для нее результат действия Sˆ2 , хотя он ясен из предыдущего:

+22 α2(1)α1(2)− 22 α2(2)α1(1)+ 22 iα2(1)(−i)α1(2)−

−22 iα2(1)(−i)α1(2)− 22 α1(1)α2(2)+ 22 α1(2)α2(1) = 0

Таким образом, антисимметричная функция является собственной операторов Sˆ2 и Sˆz , с квантовыми числами S=0 и MS=0. О таких состояниях условно говорят, что спины у них «антипараллельны» и называют их синглетными. Условно три симметричных состояния изображают схемой «а», а антисимметричное схемой «б».

179

ЛЕКЦИЯ 25

§65 Молекула водорода в приближении теории возмущений.

Кулоновский и обменный интегралы. Поведение потенциальной энергии системы двух атомов водорода для синглетного и триплетного состояний электронов. Ковалентная химическая связь

Пользуясьтеориейвозмущений(методГайтлераиЛондона), рассмотрим основное состояние молекулы водорода. Сделаем некоторые упрощения.

Первоеупрощение–будемсчитатьядранеподвижными,исходя из того, что массы ядер М велики по сравнению с массой электронов, их кинетические энергии малы , поэтому в уравнении

лапласиан по координатам ядер а и b).

Полная потенциальная энергия включает кулоновские взаимодействия ядер друг с другом, электронов 1 и 2 друг с другом, и электронов с ядрами:

где 1 и 2 – лапласианы по координатам первого и второго

180