kvant_mech

ψ(x) ≈[a1(E)+ Aa2(E)]eik2x +[b1(E)+ Ab2(E)]e−ik2x =

=αeik2x + βe−ik2x

Если поток частиц падает на область потенциала слева, то при х →+ отраженная волна должна отсутствовать, следова-

тельно, β = b1(E)+ Ab2(E) = 0, A = –b1/b2 и

α= a1(E)+ Aa2(E) =[a1(E)b2(E)−a2(E)b1(E)]/b2(E).

Вэтой задаче не возникает уравнения, определяющего энергию,ионаможетприниматьлюбыезначения.Приинфинитном движении энергия не квантуется.

ψ ≈ eik1x + Ae−ik1x . При х →+ ,т.к.U2 –Е>0,линейнонезави- симыми решениями уравнения Шредингера будут: eλ2x и e−λ2x

ψ(x) ≈[a1(E)+ Aa2(E)]eλ2x +[b1(E)+ Ab2(E)]e−λ2x =

=αeλ2x + βe−λ2x

При х →+ , решение с eλ2x не имеет физического

Е<U2, на глубину x~λ2–1.

Итак, в случае полуфинитного движения частица может удаляться на большое расстояние в область x<0, где Е>U1 Уравнения для энергии мы опять не получаем, она принимает любые значения в интервале (U2, U1). Квантование отсутствует.

51

3. U2>U1>Е. Теперь при х→- асимптотические представ-

ления будут: ϕ1=eλ1x и ϕ2=e−λ1x . Тогда ψ ≈ eλ1x + Ae−λ1x и необходимоАположитьравнымнулю,чтобыфункциябылаограни-

чена при х→- . На другом конце интервала

ϕ1(x) = a1(E)eλ2x +b1(E)e−λ2x и ϕ2 (x) = a2 (E)eλ2x +b2 (E)e−λ2x

Теперь, поскольку А=0,

ψ(x) ≈[a1(E)+ Aa2(E)]eλ2x +[b1(E)+ Ab2(E)]e−λ2x =

=a1(E)eλ2x +b1(E)e−λ2x

Решение должно затухать при х →+ , поэтому необходи-

мо, чтобы a1(E)=0. Т.к. a1(E) при заданном потенциале вполне определенная функция энергии, мы получаем уравнение для определения энергии, которое в общем случае имеет конечное или бесконечное число корней Е1, Е2, Е3,…Еn,…

Итак мы доказали следующую теорему: «При инфинитном и полуфинитном движении энергия не квантуется и изменя-

ется, как и в классической механике, непрерывно (рассеяние,

отражение). При финитном движении энергия квантуется и существуют дискретные уровни энергии» Е1, Е2, Е3,…Еn,…

Говорят о сплошном и дискретном спектре энергий.

Эта теорема может быть обобщена на трехмерный случай: Если движение финитно, Ψ→0 при r→ (по любому на-

+∞

правлению), то энергия квантуется. В этом случае ∫∫∫ψ 2 dV

−∞

сходится и волновую функцию можно нормировать так, что

+∞

∫∫∫ψ 2 dV =1. В этом случае нормированная |Ψ|2dV=Ψ*ΨdV

−∞

есть вероятность пребывания частицы в объеме dV.

52

При инфинитном движении существуют такие направления, вдоль которых Ψ остается конечной величиной при r→ . Энергия в этом случае не квантуется, интеграл расходится, и |Ψ|2dV можно трактовать лишь как пропорциональную вероятности величину, а отношение ψ 2 (r1)dV1 /ψ 2 (r2 )dV2, равно отношению соответствующих вероятностей.

§21 Квантование и биологическая эволюция

Что было бы, если бы молекулы, в том числе биологические, подчинялисьбызаконамклассическоймеханики?Вэтомслучае было бы достаточно ничтожного воздействия, чтобы изменить состояние молекулы. В результате наследственная информация менялась бы слишком часто и жизнь не могла бы существовать. Типичные расстояния между уровнями энергии ∆E молекул имеют порядок величины 1 10 эВ ~ 10-12 10-11эрг.

Почему природа не использует молекулы с более прочной связью? Ответ на этот вопрос дает распределение Больцмана, согласно которому вероятность перехода в другое со-

−∆E

стояние пропорциональна e kT . При комнатной температуре

чтобывероятностьпереходаизмениласьве24 ~1010 раз!Т.к.эволюция происходит в результате мутаций, т.е. флуктуационных измененийвструктуреДНК,товостолькожеразизмениласьбы частота мутаций.

Таким образом, требования устойчивости биологических видов ограничивают ∆E снизу, а требование достаточной скорости эволюции – сверху. В результате возможные значения ∆E (так же, как и температуры!) лежат в довольно узком интервале.

53

Простейшие задачи квантовой механики

ЛЕКЦИЯ 8

§21 Частица в потенциальном ящике с непроницаемыми стенками.

Осцилляционная теорема (без доказательства). Принцип соответствия

Рассмотрим частицу в «ящике» с непроницаемыми (бесконечными) стенками. Для этого случая потенциальная энергия будет иметь вид:

Общеерешение:ψ(x) = Asinkx + B coskx.ИзΨ(0)=0,следует

условия нормировки:

54

Отсюда для волновых функций и плотности вероятности имеем:

т, к. Ψn вещественны, то все состояния в “ящике” бесстоковые j=0, что естественно в силу полной симметрии задачи относительно точки а/2.

Последние формулы дают возможность установить еще два важных свойства Ψ-функций:

1.ФункцияΨn,описывающаясостояниеспорядковымномеромn, напромежутке(0<x<a )обращаетсявнульn –1раз.Это свойство справедливо и в общем случае финитного движения и составляет существо «осцилляционной теоремы», доказательство ее выходит за рамки нашего курса.

2.Рассмотрим усреднение ρn(x) = |Ψn|2 по быстрым осцилляциям:

физики положение частицы в «ящике» равноверятно, и поэто-

55

При n 1 квантованием энергии можно пренебречь, т. к. несмотря на то, что спектр "расползается", поскольку разность уровней энергии ∆Е пропорциональна (n+1)2–n2=2n–1, относительная разность уровней энергии с ростом n убывает:

Поэтому при n 1 квантово-механические результаты совпадают с классическими. Это утверждение составляет существо принципа соответствия и имеет весьма общий характер.

§22 Гармонический осциллятор.

Повышающий и понижающий операторы, спектр энергии.

Нулевые колебания. Распределение вероятности для слабо и сильно возбуждённых состояний

Рассмотрим частицу в поле соответствующем упругой силе, вида:

U (x) = kx2 = mω2 x2

2 2

В классической механике такая частица движется в соответствии с уравнением свободных колебаний:

следовательно, движение финитно. В квантовой механике волновые функции должны затухать при х→± , а спектр должен быть дискретным.

56

Уравнение Шредингера для такого поля:

рассматривать как некоторый оператор. Для решения этого уравнения воспользуемся приемом, напоминающим известную

57

Отметим, что произведение операторов в данном случае не

подчиняется переместительному закону и pqˆ ˆ ≠ qpˆˆ !

Теперь уравнение Шредингера для гармонического осциллятора можно записать в двух операторных формах:

(pqˆ ˆ +α)ψ = −λψ и (qpˆˆ −α)ψ = −λψ .

λ′+ 2α, λ′+ 4α, λ′+6α,...λ′+ 2nα …Действительно, применяя к левой и правой части первого из операторных уравнений оператор qˆ , имеем: qˆ(pqˆ ˆ +α)ψ′ = −λ′qˆψ′ или

(qpˆˆ +α)qˆψ′ = −λ′qˆψ′ и (qpˆˆ −α)qˆψ′ = −(λ′+ 2α)qˆψ′

Мы получили второе операторное уравнение Шредингера для ψ′′ = qˆψ′и λ′′ = λ′+ 2α . qˆ называется повышающим опе-

58

ратором, поскольку, действуя на ψ′, он повышает значения λ′ на 2α.

Аналогично можно доказать, что pˆ является понижающим оператором:

pˆ(qpˆˆ −α)ψ′= −pˆλ′ψ′ или (qpˆˆ −α)pˆψ′=−λ′pˆψ′ и

(qpˆˆ +α)pˆψ′ = −(λ′−2α)pˆψ′.

Таким образом, ряд возможных значений λ и соответствующих им волновых функций имеют вид:

Т.к. λ 0 слева последовательность должна обрываться, т.е. должна существовать такая ψ0 = pˆ lψ′, что pˆψ0 = 0. Тогда

и qpˆˆψ0 = 0, и из второго операторного уравнения следует λ0 =α,откудаследует: 2mE2 0 = mω и E0 = 2ω ..Еслирас-

шифровать pˆψ0 = 0,согласноопределению pˆ ,томыполучим

Остальные волновые функции могут быть найдены с по-

59

En = (n +1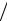2) ω.

Поэтому имеем ряд функций и соответствующих им значений энергии:

Если продолжить этот процесс мы всегда будем получать

экспоненту, умноженную на полином степени n, т.е. можно все записать так:

60