Высшая математика

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Определение 7. Непрерывной кривой L в Rm назовем множество точек, координа-

где ϕi (t) [α,β] (i = 1,..., m). При t = α, β получаем начало и конец кривой (Будем говорить, что начало и конец соединены непрерывной кривой).

Определение 8. Множество из Rm называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат этому множеству.

Замечание. Часто в определение области включают требование связности.

Определение 9. Множество называется ограниченным, если оно содержится в некотором шаре.

9.2. Последовательности точек из Rm.

Определение 1. Пусть каждому натуральному числу n поставлена в соответствие некоторая точка Mn Rm (не обязательно различные точки для разных n). Тогда множество точек M1, M2, ..., Mn, ..., взятых в указанном порядке, называется последовательностью {M n } точек из пространства Rm.

Определение предела последовательности точек из Rm по своей структуре не отличается от определения в одномерном случае:

последовательность {M n } сходится к т. А Rm, если начиная с некоторого номера,

все элементы последовательности попадают в любую наперед заданную окрестность т.А. (Точка А называется пределом последовательности, а последовательность – сходящейся). Используя логическую символику определение предела последовательности можно записать в следующей форме

( )def ( )( + ) ( ( ) )

Опр. 2 lim M n = A ≡ ε > 0 N Ν : n > N ρ M n , A < ε

n→∞

201

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

На этом примере мы видим, что не только последовательность сходится к началу координат, но и каждая координата Mn имеет нулевой предел. В общем случае справедливо

Утв. 1 Для того, чтобы последовательность {M n } ≡ {(x1(n) ,..., x(mn) )}

сходилась к точке А(а1, ..., аm), необходимо и достаточно, чтобы

lim x(n) = a i (i = 1, 2, ..., m).

n→∞ i

Доказательство:

координат точек Mn сходятся соответственно к а1, ..., аm.

Опр. 3 Последовательность {M n } называется ограниченной, если все ее элементы содержаться в некотором шаре.

Опр. 4 Пусть n1, n2, ..., nk, ... – произвольная строго возрастающая последовательность натуральных чисел, тогда последовательность M n1 ,M n2 , ... , M n k , ... называется

подпоследовательностью последовательности {M n } .

202

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Замечание: Если последовательность имеет предел, то и любая ее подпоследовательность имеет предел.

Теорема 1. Из любой ограниченной последовательности точек из Rm можно выделить сходящуюся подпоследовательность.

чена (но не имеет предела). x2

9.3. Понятие функции нескольких переменных

Опр. 1 Если каждой точке М множества {M n } из Rm поставлено в соответствие

вещественное число u, то говорят, что на этом множестве определена функция u=f(M) (или u=f(x1, ..., xm)). Множество {M n } называется областью определения функции.

Пример 1. u = a 2 − x2 − y2 . Область определения находим из условия a2-x2-y2

≥ 0 x2 + y2 ≤ a2.

Пример 2. u = ln (z – x2 – y2). Следовательно, область определения расположена над эллиптическим параболоидом z = x2 + y2.

Опр. 2 Графиком функции u=f(M) называется совокупность точек

(M, f(M)), M {M n } . График функции u=f(M) является гиперповерхностью в пространстве Rm+1.

203

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Пример 3. z = x2 + y2 +1. График функции имеет вид z

y

1

x

Опр. 3 Множество точек М(х1, ..., хm) пространства Rm, удовлетворяющих уравнению f(x1, ..., xm) = C , где С – const, называется множеством уровня функции f.

Линии уровня (m = 2) и поверхности (m = 3) дают информацию о поведении функции.

Пример 4. z = x2 +y2 +1. Линии уровня имеют вид:

y

C=2

Пример 5. u = x2 + z2 – y2 . Поверхности уровня имеют уравнения С = 0 x2 + z2 – y2 = 0 – конус;

С> 0 x2 + z2 – y2 = C – семейство однополостных гиперболоидов;

С< 0 x2 + z2 – y2 = C – семейство двухполостных гиперболоидов.

9.4. Предел функции нескольких переменных

Пусть функция u=f(M) определена на множестве {M n } Rm и т. А обладает свойством, что в любой ее окрестности есть точки из {M n } (отличные от А, если А {M n } ).

Сама точка А может не принадлежать области определения функции u=f(M). Определение предела функции нескольких переменных по своей структуре не от-

личается от определения предела функции одной переменной. Основное содержание его: если аргумент М мало отличается от А, то значение функции f(M) мало отличается от b (предела функции). Определения предела функции нескольких переменных по Гейне и Коши имеют вид:

Опр. 1*

вается пределом функции u=f(M) при М→А, если для любой последовательности {M n }

точек из {M}, сходящейся к т.А (Mn ≠ A), соответствующая последовательность значений функции {f(M n )} сходится к b.

204

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Опр. 1

def

b = lim f(M) ≡ ( ε > 0)( δ > 0):( M {M})[0 < ρ(M, A) < δ f(M) − b < ε]. Число b

M →A

называется пределом функции u=f(M) при М→А, если для любого ε>0 существует такое δ>0, что для всех точек М {M}, удовлетворяющих условию 0<ρ(M,A)<δ, справедливо

неравенство f(M) − b < ε.

Замечание 1. Иногда пишут lim f(x1,..., xm ) = b .

...x1→a1 xm →a m

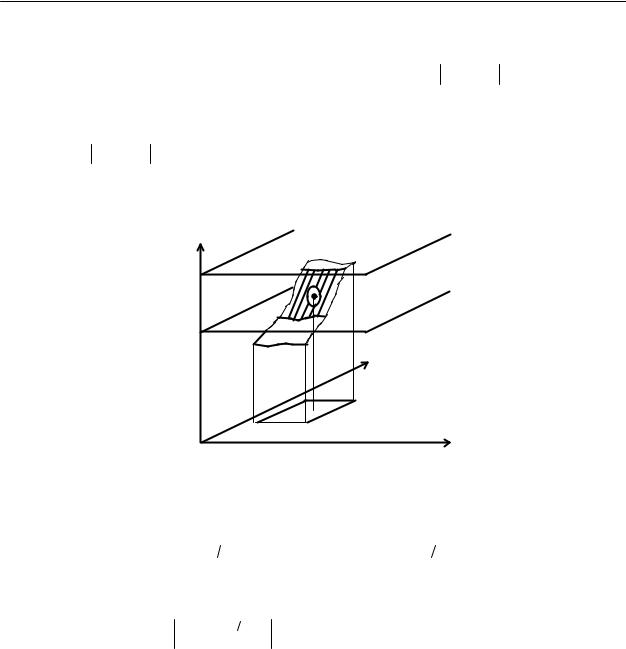
U

b+ε b

b-ε

x2

{M}

Qz(A) A

x1

На рисунке дана иллюстрация определения предела по Коши для случая m=2. Для любого ε>0 существует такая проколотая δ-окрестность т.А, значения функции в которой отличаются от b меньше, чем на ε (другими словами, график функции попадает в ε-полосу плоскости u=b).

0 < (x2 + y 2 )12 < δ (x2 + y 2 )14 < ε.

Очевидно, можно положить δ=ε2.

Заметим, что если существует предел функции u=f(M) при М→А, то существуют пределы f(М), когда М стремится к т.А вдоль любого луча, причем все эти пределы одинаковы и совпадают с пределом функции. Следовательно, если для функции удается указать, по крайней мере, два направления, вдоль которых пределы функций различны, то предела у функции нет.

Пример 2.

205

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Для этой функции вдоль осей Оx и Oy пределы существуют и равны 0 (на координатных осях функция равна 0), но вдоль прямой y=kx

y =kx

Отсюда получаем, что предела в нуле этой функции нет.

Возникает вопрос, будет ли функция нескольких переменных иметь предел, если все пределы вдоль лучей будут одинаковы? Ответ отрицательный, что видно из следующего примера.

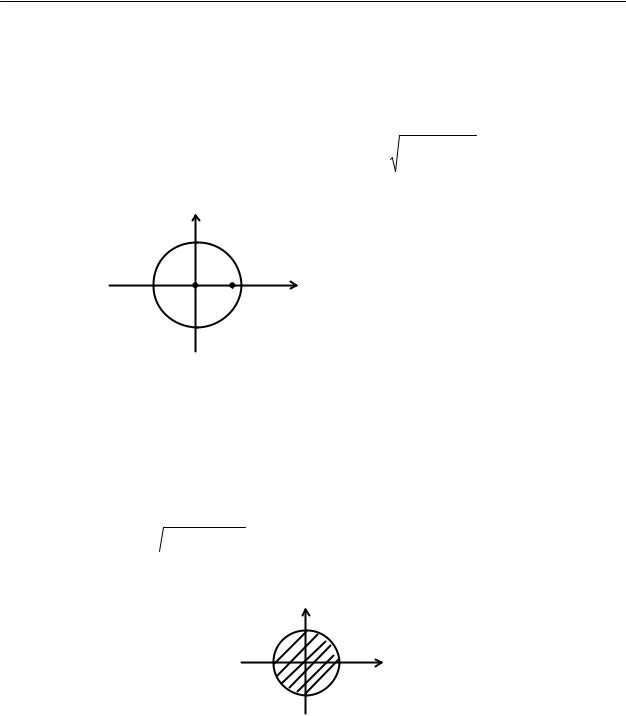
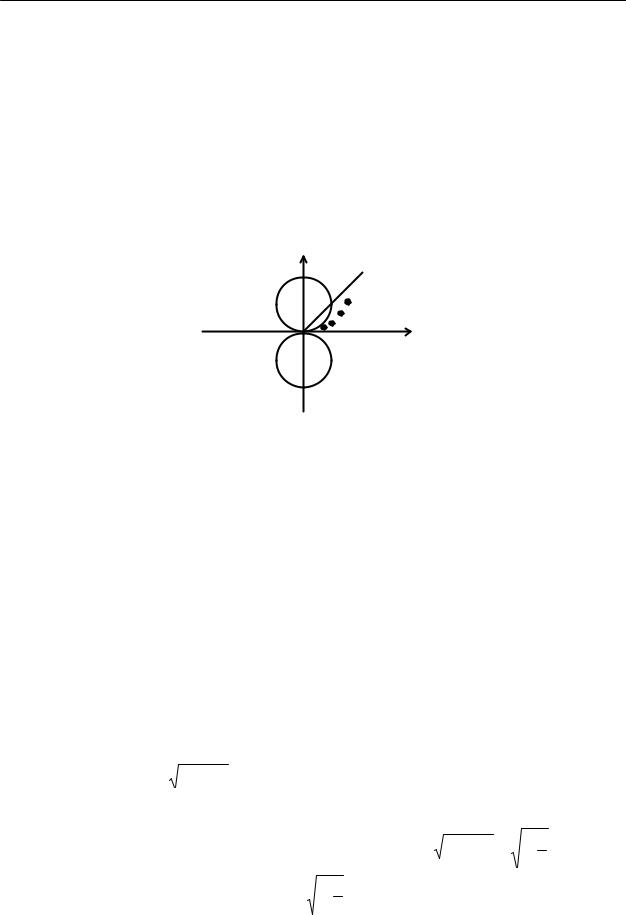
Пример 3. Функция равна 1 на оси Ох и двух кругах радиуса 1, касающихся оси Ох в начале координат, в остальных точках она равна 0 (см. рис.)

Любой луч, кроме Ох, идущий в начало координат, попадает в круг, а там функция равна 1, следовательно, предел вдоль любого луча равен 1. С другой стороны, есть последовательности точек, расположенных между осью Ох и окружностью

тельно, предел ее вдоль таких последовательностей равен нулю. Отсюда получаем, что предела в нуле функция не имеет.

206

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Замечание 2. Для пределов суммы, разности, произведения и частного функций нескольких переменных справедливы те же формулы, что и в одномерном случае.

9.5. Непрерывность функции нескольких переменных

Определение 1. Функция u=f(M) называется непрерывной в т. А, если lim f(M) = f(A) .

M →A

Определение 2. Функция u=f(M) называется непрерывной на множестве {M}, если она

непрерывна в каждой точке этого множества.

Условию непрерывности можно придать разностную форму. Пусть

∆u ≡ f(x1,..., xm ) − f(a1,...,a m ) ≡ f(a1 + ∆x1,...,a m + ∆xm ) − f(a1,...,a m ) ,

тогда условие непрерывности имеет вид:

lim ∆u = 0 .

∆x1→0,...,∆xm →0

(В примере 1 предыдущей темы рассмотрена непрерывная в нуле функция.)

Фиксируем все переменные, кроме одной, проложив, например, х2=а2,..., хm=аm. Тогда получим функцию одной переменной f(x1,a2,...,am), которая будет непрерывной в т. х1=а1, если f(x1,...,xm) непрерывна в т. А (очевидно). Таким образом, из непрерывности функции нескольких переменных в точке следует ее непрерывность по каждой координате (при фиксированных остальных). Обратное утверждение неверно, что показывает пример 2 предыдущей темы:

На координатных осях функция непрерывна (просто тождественно равна 0), но даже не имеет предела в т. (0,0). Непрерывности вдоль лучей также не достаточно для непрерывности в точке функции нескольких переменных. Это показывает пример 3 предыдущей темы.

9.5.1.Основные свойства непрерывных функций

1.Арифметические операции над непрерывными функциями приводят к непрерывным функциям (для частного знаменатель отличен от нуля).

2.Непрерывность сложной функции.

u = f(ϕ1(t1,..., t k ),..., ϕm (t1,..., t k )) , т.е. на множестве Т определена функция, которую мы назовем сложной функцией.

207

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Пример 1. u = ex+y2 ; y=t ; x=t+s, тогда сложная функция имеет вид u = et2 +t+s .

Теорема. Пусть имеет смысл сложная функция f(ϕ1, ..., ϕm). Если функции ϕ1, ..., ϕk непрерывны в т. (t10,..., t 0k ) ≡ t (0) , а функция f непрерывна в т. x(0) ≡ (ϕ1(t (0) ),..., ϕm (t (0) )),

тогда сложная функция f(ϕ1, ..., ϕk) непрерывна в т. t(0).

По этой теореме функция et2 +t+s непрерывна при всех (t,s) R2.

3. Устойчивость знака непрерывной функции.

Теорема. Пусть функция u=f(M) непрерывна в т.А и f(A)≠0. Тогда существует такая δ-окрестность т.А, в которой f(M) имеет тот же знак, что и f(A).

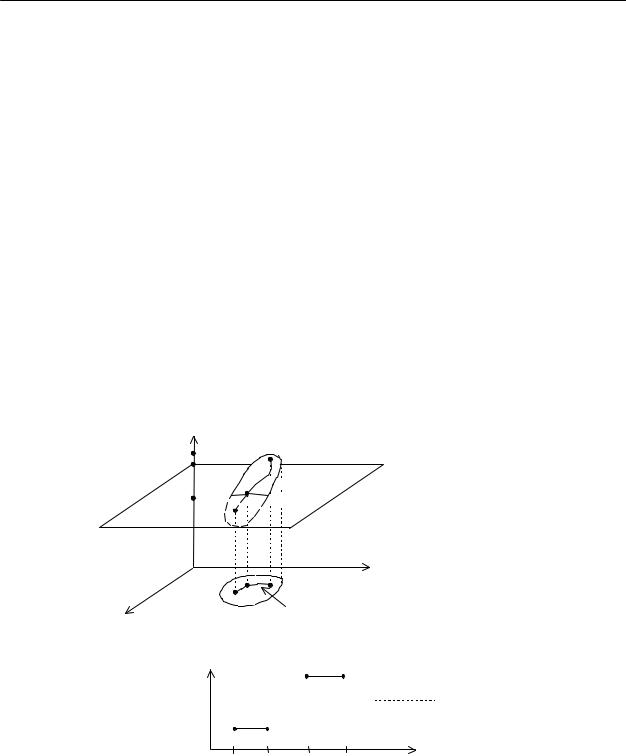
4. Прохождение непрерывной функции через любое промежуточное значение. Теорема. Пусть функция u=f(M) непрерывна на связном множестве {M}. Тогда

для любых точек А, В {M} и для любой кривой, L, соединяющей эти точки и лежащей в {M}, найдется точка на этой кривой, в которой функция принимает любое заданное промежуточное значение между f(A) и f(B).

u

f(B)

C

f(A)≤C≤f(B) f(A)

K L, f(K)=C

y

Условие связности существенно уже в одномерном случае: u

c

5.Теоремы Вейерштрасса.

Теорема 1. Функция, непрерывная на ограниченном замкнутом множестве, ограничена на этом множестве.

Теорема 2. Функция, непрерывная на ограниченном замкнутом множестве, достигает на этом множестве своих точных верхней и нижней граней. Для неограниченных или не замкнутых множеств эти утверждения неверны уже в одномерном случае.

208

9.ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

9.6.Дифференцируемость функций нескольких переменных

1.9.6.1.Частные производные функций нескольких переменных

Пусть М(х1, х2, ..., хm) внутренняя точка области определения функции u=f(x1, ..., xm). Пусть ∆xk – приращение k-ой координаты в данной фиксированной т.М, ему соответствует частное приращение функции

∆xk u ≡ f(x1, ..., xk-1, xk+∆xk, xk+1, ..., xm) – f(x1, ..., xm).

Рассмотрим отношение ∆xk u , которое зависит от ∆xk и определено при всех дос-

∆xk

таточно малых ∆xk, отличных от нуля.

Определение 1. Если существует lim ∆xk u , то он называется частной производ-

∆x→0 ∆xk

ной функции u=f(x1, ..., xm) в т. М(x1, ..., xm) по аргументу xk и обозначается одним из сим-

как функции только k-й переменной (при фиксированных остальных переменных). Это позволяет вычислить частные производные по одной из переменных по обычным формулам дифференцирования, если зафиксировать все остальные переменные.

Пример 1. u = x2 + 3xy – y

Пример 2. u = ex2 −y2

∂∂ux = ex2 −y2 (+2x) (при фиксированном у применима обычная теорема о произ-

Выясним теперь, насколько полную информацию дают частные производные функции в данной точке о поведении функции в окрестности этой точки.

209

9. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Сразу отметим, что частные производные в т.М0 могут дать информацию о поведении функции только на прямых, проходящих через т.М0 и параллельных координатным осям.

М0

Конечно, этой информации совсем не достаточно, чтобы судить о поведении функции в целой окрестности т.М0 (и, в частности, на других лучах, проходящих через т.М0).

существуют и обращаются в нуль не только в т. (0,0), но и всюду на координатных осях, а сама функция не имеет в т. (0,0) предела (см. тему 4). Заметим, что в одномерном случае из существования производной следовала непрерывность функции.

Таким образом, мы приходим к необходимости ввести более сильное условие, чем существование частных производных, чтобы оно было аналогом дифференцируемости функции одной переменной. Это условие должно быть связано с полным приращением функции в точке.

9.6.2. Дифференцируемость функции нескольких переменных

Определение 2. Функция u=f(x1, ..., xm) называется дифференцируемой в точке M(x1, ..., xm), если ее полное приращение в этой точке может быть представлено в виде

f(x1+∆x1, ..., xm+∆xm) – f(x1, ..., xm) ≡

≡ ∆u = A1∆x1 + A2∆x2 + ... + Am∆xm + α1∆x1 + ... + αm∆xm,

где А1, А2, ..., Аm – некоторое, не зависящие от ∆x1, ..., ∆xm, числа,

а α1, α2, ..., αm – бесконечно малые при ∆x1→0, ..., ∆xm→0 функции, равные 0 при

∆x1=∆x2=... =∆xm=0.

Если положить ρ = ∆x12 +...+∆x2m , то условие дифференцируемости может быть

записано в виде:

∆u = A1∆x1 + A2∆x2 + ... + Am∆xm + )(ρ) (1)

Оба представления эквивалентны и означают, что приращение функции представимо в виде линейной части (по ∆x1, ..., ∆xm) и членов более высокого порядка (по ∆x1, ...,

∆xm или ρ).

Теорема 1. Если функция u=f(x1, ..., xm) дифференцируема в точке

210