Fizika_tyazhelykh_ionov

Из выражения (11.34) видно, что за счет выбора ω расстояние между правым частями u1 и u2 можно сделать сколь угодно малым

(под знаком интеграла стоит быстро осциллирующая знакопеременная функция). В то же время, расстояние между соответствующими решениями (11.35) может быть сколь угодно большим, что и демонстрирует отсутствие устойчивости. Полезно зафиксировать полученный результат в рамках следующего определения.

Пусть определено понятие «решение» и (любому) элементу u U отвечает единственное решение z = R(u) из пространства F.

Задача нахождения z называется устойчивой на пространствах (F, U) если для ε > 0 (существует) δ(ε)> 0 такое, что из ус-

ловия ρu (u1,u2 )≤ δ(ε) cледует, что ρF (z1, z2 )≤ ε .

В свою очередь: задача определения решения z из F по «исходным данным» u из U называется корректно поставленной на паре метрических пространств (F, U), если:

—для u U z F ;

—решение определено однозначно;

—задача устойчива на (F, U).

Таким образом, задача нахождения решения уравнения Фредгольма (11.30) является примером некорректно поставленной задачи. Следует подчеркнуть, что в соответствии с приведенными определениями устойчивость и корректность задачи зависят от выбора метрики функциональных пространств, на которых она рассматривается.

11.5.1. Регуляризирующий оператор

Решение некорректно поставленных задач потребовало нового подхода, впервые развитого академиком Тихоновым в рамках функционального анализа. Целью дальнейшего изложения является

390

неформальное ознакомление читателя с идеями и алгоритмами, предложенными для решения уравнения Фредгольма (11.31).

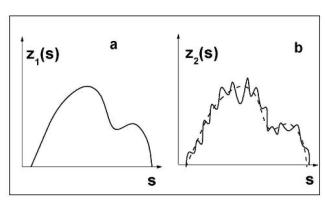
Прежде всего, более детально обсудим причину возникновения неустойчивости решения обратной задачи. Пусть решение z1 (s)

выглядит так, как показано на рис.11.12, а. Функция z2 (s) получена из z1 (s) наложением знакопеременной осциллирующей функции.

Рис. 11.12. Решение уравнения Фредгольма z1 (s) (а) и близкая функция z2 (s), отличающаяся по гладкости (b)

Как уже отмечалось, интегралы от этих функций будут мало отличаться, хотя сами функции отличаются существенно. Так как

проинтегрированная с весом k (x, s) функция z (s) и есть измеряемый в эксперименте спектр u (x) , то обсуждаемое отличие в интегралах может не превышать неопределенности, с которой известна u (x) из-за погрешности ее измерения δ. Чтобы подчеркнуть это

обстоятельство, далее будем обозначать измеренный спектр как uδ (x) . Таким образом, первичным источником «неприятностей»

является неопределенность в uδ (x) , а интегральный оператор А из (11.31) позволяет «втиснуться» в эту щель очень разным функциям z (s), в том числе, имеющим физически необусловленные осцил-

391

ляции. Общая идея метода регуляризации состоит в привлечении для нахождения устойчивого решения дополнительной (априорной) информации относительно свойств будущего решения. Из

сравнения функций z1 (s) и z2 (s) ясно, что это должна быть ин-

формация о гладкости искомого решения. Техника его нахождения состоит в следующем.

Если ничего не знать о неустойчивости решения уравнения (11.31), то в рамах «наивного» подхода можно было бы искать решение как функцию, минимизирующую функционал:

аналогичный, по смыслу, исходному выражению (11.11) в методе наименьших квадратов. Однако оказывается, что находимое таким образом решение будет неустойчиво относительно малых измене-

ний правой части uδ (x).

Было предложено вместо исходной неустойчивой задачи решать близкую к ней, сводящуюся к минимизации функционала:

где α — положительный скалярный множитель, который называется параметром регуляризации, а функционал Ω[z] — тихоновским

стабилизатором.

По определению, тихоновским стабилизатором p-го порядка называется функционал вида:

где qn (s) — известные неотрицательные функции. Например, стабилизатор второго порядка в частном случае может иметь вид:

Имея в виду, что решение находится минимизацией функциона-

ла M α , можно понять роль, которую играют в процессе нахождения решения его составные части:

392

ставить в функционал M α вместо z выражение (11.41), то получим функцию от β:

и доставляет минимум функционалу M α . Выражение (11.43) представляет собой уравнение Эйлера—Лагранжа (11.40), записанное в развернутой форме. Де факто это интегро-дифференциальное уравнение, получаемое после выполнения преобразований (11.40– 11.43). Для нахождения единственного решения этого уравнения необходимо задать краевые условия, например, значения искомой функции на границах: z (a)= c1 , z (b)= c2 . В общем случае анали-

тическое решение уравнения отсутствует, поэтому его решают численно. Функции k (x, s), z (x) и u (s) заменяют на соответст-

вующие сеточные функции kij = k (xi , sj ), zi = z (xi ), u j = u (sj ) ин-

тегралы и производные приближают формулами численного интегрирования и дифференцирования. В результате уравнение (11.43) приводится к виду:

где zG — вектор решения, K — матрица и b — вектор c компонентами, зависящими только от kij , u j , а также коэффициентов, вхо-

дящих в формулы численного интегрирования. Окончательно регуляризированное решение уравнения (11.31) получается в виде:

Как уже отмечалось, функционал M α (11.37) должен быть полностью определен перед процедурой его минимизации, т. е. должны быть известны стабилизатор Ω[z] и параметр регуляризации α.

Чем более гладкое решение ожидается, исходя из априорных (физических) соображений, тем выше может быть степень используе-

394

мого стабилизатора. Один из наиболее последовательных подходов

кнахождению α будет обсужден ниже.

11.5.2.Нахождение параметра регуляризации

Для каждой из ряда αк и заданного Ω[z] найдем решение zαk (пользуясь выражением (11.45)) и поставим ему в соответствие

uαk = ∫b k (x, s)zαk ds . Построим функцию Y:

a

где S (x) — среднеквадратичная погрешность измерения спектра

uδ . Покажем, что при некоторых условиях Y распределено по χ2 .

Заменим в (11.46) интеграл суммой, а все функции на их сеточный аналог, как это уже делалось в предыдущем разделе. Тогда:

Как это уже многократно показывалось, для того, чтобы статистика Y была распределена по χ2 с n степенями свободы, требуется

выполнение трех условий: каждое слагаемое в (11.47) должно быть распределено нормально, с нулевым средним и единичной диспер-

сией. Так как случайной величиной является только вектор uδ (xk ),

то именно компоненты этого вектора должны быть распределены нормально.

Это выполняется, если измеренный спектр uδ хорошо статисти-

чески обеспечен, так что биномиальное распределение числа отсчетов в конкретном канале можно аппроксимировать нормальным.

Допустим, что выполняется второе из перечисленных условий: uαk (xk )−uδ (xk ) = 0 ,

395

тогда uδ (xk ) = uαk (xk ), но, по определению, uδ (xk ) = uT , т. е. точной правой части. Таким образом, обсуждаемое условие выполняется, если удалось выбрать такое αk , что uαk = uT .

Наконец, выполнение третьего из условий обеспечивается наличием в знаменателе дроби в формуле (11.47) Sk = D(uδ (xk )) .

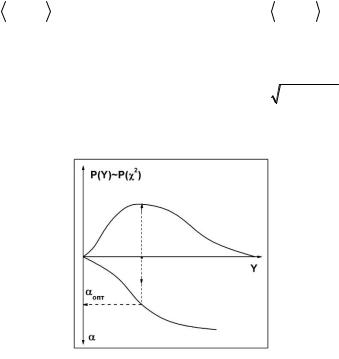
С учетом полученного, предлагается следующий алгоритм вы-

бора αопт (рис. 11.13).

Рис. 11.13. Схема выбора оптимального значения параметра регуляризации αопт

Строится зависимость Y (α), показанная в нижней части

рис. 11.13. С этой целью для каждого задаваемого значения α находится регуляризированное решение (11.45) и вычисляется Y согласно формуле (11.47). Определяем значение аргумента Ymax , со-

ответствующее максиму распределения χ2 с n степенями свободы (рис. 11.13, верхний график) и по графику Y (α) находим αопт .

11.5.3. Уравнение типа свертки

Рассмотрим, прежде всего, следующую задачу. Пусть имеется случайная величина X c функцией распределения PX и случайная

396

величина Y c функцией распределения PY . Как распределена их сумма: Z = X +Y ?

Вероятность получить конкретное z есть PZ = PX (x) PY (y), но нас устраивают только пары (x, y), дающие в сумме z, поэтому PZ = PX (x) PY (z − x). Событие z = x + y реализуется в ряде частных случаев. Для получения полной вероятности наступления этого события надо просуммировать все парциальные вероятности (формула полной вероятности), поэтому окончательно (уже для непрерывных случайных величин X и Y):

где G — область определения X. Полученное выражение называется сверткой. По смыслу задачи можно констатировать, что свертка получается тогда, когда каждое фиксированное значение одной случайной величины «размывается» одним и тем же спектром значений другой. Типичный пример — суммирование спектров сигнала и шума в электронных приборах. Выражение (11.48) можно воспринимать и как частный случай соотношения (11.29). Действительно, если функция отклика спектрометра не зависит от энергии, т. е. одна и та же для любых значений энергии, связь измеренного

спектра PZ (z) c истинным спектром PX (x) задается выражением

(11.48). Восстановление истинного спектра в этом случае сводится к решению интегрального уравнения типа свертки.

Проанализируем устойчивость задачи нахождения решения уравнения типа свертки. В обозначениях, введенных ранее в

(11.30), (11.31):

где ξ(t ) — помеха, шум, а uT (t) — точная правая часть уравнения

(11.49).

Как известно, фурье-образ свертки равен произведению фурьеобразов подынтегральных функций. Поэтому:

397

z (ω)= kz ((ωω)) = ukT((ωω)) + ζk ((ωω))

Естественным выглядит желание в качестве решения уравнения (11.49) взять обратное фурье-преобразование от выражения (11.51):

Определенная таким образом функция z (t) может и не существовать из-за расходимости второго слагаемого в (11.52). Действительно, так как k (ω)→ 0 и ζ(ω)→ 0 при ω→ ∞ , но это стремление к нулю несогласованное — фурье-образ шума ζ(ω) спадает с ростом частоты медленнее, чем фурье-образ функции отклика k (ω). Таким образом, и обсуждаемая задача является неустойчи-

вой.

Для получения устойчивого решения (обеспечения сходимости второго слагаемого в (11.52)) необходимо «задавить» влияние вы-

u (ω)

соких частот. Для этого можно умножить дробь k (ω) на некото-

рый множитель f (ω,α), зависящий от параметра α — как это и должно быть при введении регуляризирующего оператора. В качестве f (ω,α) часто выбирают функцию вида:

где L(ω)= k (ω)k (−ω), а M (ω) — произвольная четная положительная функция.

398

Регуляризированное решение уравнения (11.49) определяется формулой:

p

Полагая M (ω)= ∑qnω2n , где qn — заданные неотрицательные

n=0

константы, получаем по выражению (11.55) тихоновские стабилизаторы порядка p. Практика показывает, что почти всегда доста-

точно полагать M (ω)= ω2 .

Определение параметра регуляризации. В принципе, подходы к нахождению α, развитые для решения уравнения Фредгольма первого рода с ядром общего вида (см., в частности, раздел 11.5.2), работают и для уравнения типа свертки. Вместе с тем, именно здесь удобно продемонстрировать тот факт, что регуляризация чревата внесением в решение ошибок метода.

Рассмотрим разность:

уклонение, связанное с ошибкой правой части уравнения (11.49). Можно показать, что

1 → 0 , 2 → ∞ при α → 0 .

399