
ЛР Численные методы (Трухачев)
.pdfВариант 3.9
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
3,91 |
4,45 |
5,83 |
7,18 |
8,78 |
10,75 |
11,82 |
yi |
-6,74 |
-7,12 |
-6,50 |
-5,83 |
-4,91 |
-5,91 |
-5,65 |
Метод решения СЛАУ: решение СЛАУ через поиск обратной матрицы (обратная матрица рассчитывается с помощью метода Гаусса).
Вариант 3.10
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
0,67 |
1,16 |
2,94 |
3,04 |
3,74 |
3,99 |
0,67 |
yi |
-19,66 |
-20,23 |
-20,29 |
-20,12 |
-21,03 |
-20,75 |
-19,66 |
Метод решения СЛАУ: метод Крамера (определители матриц рассчитываются с помощью метода Гаусса).
Вариант 3.11
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
1,13 |
2,47 |
3,09 |
3,86 |
3,99 |
4,91 |
1,13 |
yi |
11,74 |
11,42 |
10,45 |
10,42 |
9,98 |
10,50 |
11,74 |
Метод решения СЛАУ: классический метод Гаусса.
Вариант 3.12
Степень аппроксимирующего полинома: m=2. Таблица приближенных значений функции:
xi |
12,00 |
12,28 |
12,41 |
13,39 |
13,97 |
15,10 |
16,40 |
yi |
-1,69 |
-2,17 |
-2,47 |
-2,41 |
-1,68 |
-0,89 |
-0,54 |
Метод решения СЛАУ: решение СЛАУ через поиск обратной матрицы (обратная матрица рассчитывается с помощью метода Гаусса).
71
Вариант 3.13
Степень аппроксимирующего полинома: m=4. Таблица приближенных значений функции:
xi |
5,05 |
5,89 |
5,91 |
7,22 |
7,54 |
8,29 |
9,13 |
yi |
8,12 |
7,81 |
7,72 |
7,38 |
7,55 |
7,00 |
7,45 |
Метод решения СЛАУ: метод Крамера (определители матриц рассчитываются с помощью метода Гаусса).
Вариант 3.14
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
1,06 |
2,93 |
3,96 |
5,45 |
6,55 |
6,69 |
8,16 |
yi |
-16,00 |
-15,54 |
-15,27 |
-15,39 |
-15,52 |
-14,86 |
-14,55 |
Метод решения СЛАУ: классический метод Гаусса.
Вариант 3.15
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
-2,66 |
-2,26 |
-0,29 |
1,14 |
3,03 |
3,11 |
-2,66 |
yi |
-17,87 |
-17,11 |
-17,31 |
-16,82 |
-17,39 |
-17,82 |
-17,87 |
Метод решения СЛАУ: решение СЛАУ через поиск обратной матрицы (обратная матрица рассчитывается с помощью метода Гаусса).
Вариант 3.16
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
14,09 |
16,04 |
17,22 |
17,36 |
18,32 |
19,39 |
21,05 |
yi |
-14,28 |
-13,59 |
-12,74 |
-12,73 |
-13,69 |
-14,21 |
-13,70 |
Метод решения СЛАУ: метод Крамера (определители матриц рассчитываются с помощью метода Гаусса).
72
Вариант 3.17
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
7,91 |
9,61 |
10,44 |
11,05 |
11,93 |
12,90 |
14,34 |
yi |
17,59 |
18,07 |
17,39 |
16,82 |
17,30 |
18,27 |
17,73 |
Метод решения СЛАУ: классический метод Гаусса.
Вариант 3.18
Степень аппроксимирующего полинома: m=4. Таблица приближенных значений функции:
xi |
3,12 |
5,09 |
6,01 |
6,07 |
7,43 |
9,12 |
3,12 |
yi |
-15,06 |
-14,10 |
-14,95 |
-15,47 |
-15,18 |
-15,79 |
-15,06 |
Метод решения СЛАУ: решение СЛАУ через поиск обратной матрицы (обратная матрица рассчитывается с помощью метода Гаусса).
Вариант 3.19
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
-17,91 |
-17,49 |
-16,47 |
-16,28 |
-14,76 |
-13,62 |
-13,53 |
yi |
2,15 |
2,76 |
3,27 |
3,18 |
3,87 |
3,62 |
2,66 |
Метод решения СЛАУ: метод Крамера (определители матриц рассчитываются с помощью метода Гаусса).
Вариант 3.20
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
15,53 |
17,41 |
17,42 |
18,91 |
19,91 |
20,56 |
20,84 |
yi |
-11,63 |
-11,23 |
-11,20 |
-11,44 |
-12,25 |
-12,81 |
-13,00 |
Метод решения СЛАУ: классический метод Гаусса.
73
Вариант 3.21
Степень аппроксимирующего полинома: m=4. Таблица приближенных значений функции:
xi |
-9,58 |
-8,90 |
-7,92 |
-7,81 |
-6,34 |
-5,12 |
-4,34 |
yi |
17,14 |
16,28 |
15,48 |
15,04 |
15,25 |
14,41 |
14,87 |
Метод решения СЛАУ: решение СЛАУ через поиск обратной матрицы (обратная матрица рассчитывается с помощью метода Гаусса).
Вариант 3.22
Степень аппроксимирующего полинома: m=2. Таблица приближенных значений функции:
xi |
3,20 |
4,96 |
5,46 |
5,82 |
7,34 |
8,91 |
9,29 |
yi |
-5,77 |
-6,68 |
-6,54 |
-7,14 |
-8,00 |
-7,59 |
-8,51 |
Метод решения СЛАУ: метод Крамера (определители матриц рассчитываются с помощью метода Гаусса).
Вариант 3.23
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
2,80 |
4,19 |
5,49 |
6,24 |
7,35 |
9,04 |
10,05 |
yi |
18,80 |
19,48 |
19,45 |
19,09 |
19,67 |
19,69 |
18,95 |
Метод решения СЛАУ: классический метод Гаусса.
Вариант 3.24
Степень аппроксимирующего полинома: m=3. Таблица приближенных значений функции:
xi |
-7,62 |
-7,14 |
-5,37 |
-3,77 |
-2,34 |
-0,86 |
-7,62 |
yi |
9,64 |
10,06 |
10,16 |
10,82 |
11,01 |
11,33 |
9,64 |
Метод решения СЛАУ: решение СЛАУ через поиск обратной матрицы (обратная матрица рассчитывается с помощью метода Гаусса).
74

Вариант 3.25
Степень аппроксимирующего полинома: m=4. Таблица приближенных значений функции:
xi |
18,87 |
19,83 |
20,82 |
21,16 |
22,88 |
24,29 |
24,85 |
yi |
-13,92 |
-14,31 |
-15,13 |
-16,07 |
-16,97 |
-16,79 |
-16,60 |
Метод решения СЛАУ: метод Крамера (определители матриц рассчитываются с помощью метода Гаусса).
|
Варианты заданий к работе 4 |
|
||||||
Вариант 4.1 |
|
|
|
|
|
|
|
|
Функция f(x): |
1 |
. |
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
1 + x2 |
|
|
|
||
Точка расчета: |
x=1. |
|
|
|
||||
Формула |
аппроксимации |
значений |
первой |
производной: |
||||
(4.1). |
|
|
|
|
|
|
|
|
Уровень абсолютных погрешностей значений функции: |
||||||||
∆=7×10-6. |
|
ε=8×10-4. |
|
|
|
|||
Точность расчета: |
|
|
|
|
||||
Вариант 4.2 |
|
|
|
|
|
|
|
|
Функция f(x): |
|
x x . |
|
|
|
|||
Точка расчета: |
x=1. |
|
|
|
||||
Формула |
аппроксимации |
значений |
первой |
производной: |
||||
(4.2).
Уровень абсолютных погрешностей значений функции:
∆=1×10-6.
Точность расчета: ε=7×10-4.
75
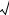
Вариант 4.3
|
|
e x |
|
Функция f(x): |
|
|
. |
1 + e2 x |
|||
Точка расчета: |
x=0. |
||
Формула аппроксимации значений первой производной:
(4.3).
Уровень абсолютных погрешностей значений функции:
∆=7×10-6.
Точность расчета: ε=3×10-4.
Вариант 4.4
|
1 |
|
− |
x 2 |
|
|||
Функция f(x): |
|
|
|
|
e |
2 . |
||
|
|
|
|
|||||
|
|
2π |
||||||
|
|
|
|
|
|
|
|
|
Точка расчета: |
x=1. |
|
|
|
|
|
||
Формула аппроксимации |
|
значений первой производной: |
||||||
(4.4).
Уровень абсолютных погрешностей значений функции:
∆=4×10-6.
Точность расчета: ε=5×10-4.
Вариант 4.5 |
|
|
|
Функция f(x): |
|
sin x |
. |
|
|
||
|
|
x |
|
Точка расчета: |
x=-π/3. |
||
Формула аппроксимации значений первой производной:
(4.5).
Уровень абсолютных погрешностей значений функции:
∆=5×10-6.
Точность расчета: ε=5×10-4.
76
Вариант 4.6 |
|
Функция f(x): |
x × cos e x . |
Точка расчета: |
x=0. |
Формула аппроксимации значений первой производной:
(4.1).
Уровень абсолютных погрешностей значений функции:
∆=3×10-6. |
ε=9×10-4. |
Точность расчета: |
|
Вариант 4.7 |
e− x . |
Функция f(x): |
|
Точка расчета: |
x=0. |
Формула аппроксимации значений первой производной:
(4.2).
Уровень абсолютных погрешностей значений функции:
∆=3×10-6.
Точность расчета: ε=5×10-4.
Вариант 4.8 |
|
|
|
Функция f(x): |
- |
ln x |
. |
|
|||
|
1 + e x |
|
|
Точка расчета: |
x=1. |
|
|
Формула аппроксимации значений первой производной:
(4.3).
Уровень абсолютных погрешностей значений функции:
∆=6×10-6.
Точность расчета: ε=9×10-4.
77
Вариант 4.9
|
|
x2 +1 |
||
Функция f(x): |
|
|
|
. |
|
3x3 - 5x 2 |
+10 |
||
|
|
|
||
Точка расчета: |
x=1. |
|
|
|
Формула аппроксимации |
значений первой производной: |
|||
(4.4).
Уровень абсолютных погрешностей значений функции:
∆=3×10-6. |
ε=2×10-4. |
Точность расчета: |
|
Вариант 4.10 |
ln x × cos x . |
Функция f(x): |
|
Точка расчета: |
x=1. |
Формула аппроксимации значений первой производной:
(4.5).
Уровень абсолютных погрешностей значений функции:
∆=5×10-6.
Точность расчета: ε=3×10-4.
Вариант 4.11 |
|
Функция f(x): |
arctg x . |
Точка расчета: |
x=-π/4. |
Формула аппроксимации значений первой производной:
(4.1).
Уровень абсолютных погрешностей значений функции:
∆=8×10-6.
Точность расчета: ε=1×10-4.
78

Вариант 4.12 |
|
Функция f(x): |
ecos x . |
Точка расчета: |
x=0. |
Формула аппроксимации значений первой производной:
(4.2).
Уровень абсолютных погрешностей значений функции:
∆=6×10-6.
Точность расчета: ε=7×10-4.
Вариант 4.13
Функция f(x): |
1 |
e |
x |
. |
|
|
|
|
|||
|
|
x |
|
|
|
Точка расчета: |
x=1. |
|
|||
Формула аппроксимации значений первой производной:
(4.3).
Уровень абсолютных погрешностей значений функции:
∆=4×10-6.
Точность расчета: ε=7×10-4.
Вариант 4.14
Функция f(x): |
1 |
|
. |
||
|
|
|
|
||
|
1 + x2 |
||||
|
|
|
|||
Точка расчета: |
x=2. |
|
|||
Формула аппроксимации |
значений первой производной: |
||||
(4.4).
Уровень абсолютных погрешностей значений функции:
∆=1×10-6.
Точность расчета: ε=6×10-4.
79
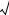
Вариант 4.15 |
|
Функция f(x): |
x x . |
Точка расчета: |
x=2. |
Формула аппроксимации значений первой производной:
(4.5).
Уровень абсолютных погрешностей значений функции:
∆=4×10-6.
Точность расчета: ε=2×10-4.
Вариант 4.16
|
|
e x |
|
Функция f(x): |
|
|
. |
1 + e2 x |
|||
Точка расчета: |
x=1. |
||
Формула аппроксимации значений первой производной:
(4.1).
Уровень абсолютных погрешностей значений функции:
∆=6×10-6.
Точность расчета: ε=6×10-4.
Вариант 4.17
|
1 |
|
− |
x 2 |
|
|||
Функция f(x): |
|
|
|
|
e |
2 . |
||
|
|
|
|
|||||
|
|
2π |
||||||
|
|
|
|
|
|
|
|
|
Точка расчета: |
x=1,5. |
|
|
|||||
Формула аппроксимации |
|
значений первой производной: |
||||||
(4.2).
Уровень абсолютных погрешностей значений функции:
∆=5×10-6.
Точность расчета: ε=5×10-4.
80
