
Пример 3.5
Найти графически
наибольшее и наименьшее значения функции
![]() в области Q,
ограниченной линиями
в области Q,
ограниченной линиями
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Используем алгоритм графического метода (информация 3.2.8).

 Построим
линии
Построим
линии
![]() ,
,
![]() ,
,
![]() ,
ограничивающие область Q.
Получим треугольник АВС (рисунок 3.4).
,
ограничивающие область Q.
Получим треугольник АВС (рисунок 3.4).
Р![]() имеют
уравнение
имеют
уравнение
![]() ,
или
,
или
![]() .
Очевидно, это параболы с вершинами в
точках
.
Очевидно, это параболы с вершинами в
точках
![]() ,
осью симметрии ОУ, ветви которых
направлены вверх. Построим несколько
линий уровня, например, при
,
осью симметрии ОУ, ветви которых
направлены вверх. Построим несколько
линий уровня, например, при
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рисунок 3.4).
(рисунок 3.4).
Нам необходимо
определить, через какую точку области
Q
пройдет линия уровня с наибольшим
возможным значением С,
а через какую – с наименьшим. Нетрудно
заметить, что с возрастанием С
вершина параболы – линии уровня –
поднимается вдоль оси ОУ все выше вверх
и последняя из этих линий, проходящая
через точки области Q,
коснется границы области в точке Р![]() .
В этой точке и достигается наибольшее
значение функции, которое равно
.
В этой точке и достигается наибольшее
значение функции, которое равно
![]() .
.
Наоборот, при
убывании значения С
вершина параболы опускается вниз, и
последняя точка области Q,
через которую пройдет линия уровня с
наименьшим значением С,
будет точка В – точка пересечения
граничных линий области. Ее координаты
можно найти, решая систему уравнений
этих линий:
 откуда
откуда
![]() ,
,
![]() .
Таким образом, точка В имеет координаты
.
Таким образом, точка В имеет координаты
![]() .
Наименьшее значение функции в заданной
области равно
.
Наименьшее значение функции в заданной
области равно
![]() .
.
З амечание.
Графический метод особенно
удобен для отыскания
наибольшего и наименьшего значений
линейной
функции
амечание.
Графический метод особенно
удобен для отыскания
наибольшего и наименьшего значений
линейной
функции
![]() .
В этом случае искомые точки лежат на
границе области и чтобы их найти,
поступают так. Строят произвольную
линию уровня (прямая) и градиент данной
функции (этот вектор, как известно,
указывает направление возрастания
функции, а для линейной функции градиент
имеет постоянное направление). Перемещая
линию уровня в направлении градиента,
находят точку границы (рисунок 3.5), через
которую линии уровня входят
в область (точка наименьшего значения
функции) и точку, через которую линии
уровня выходят
из области (точку наибольшего значения
функции).
.
В этом случае искомые точки лежат на
границе области и чтобы их найти,
поступают так. Строят произвольную
линию уровня (прямая) и градиент данной
функции (этот вектор, как известно,
указывает направление возрастания
функции, а для линейной функции градиент
имеет постоянное направление). Перемещая
линию уровня в направлении градиента,
находят точку границы (рисунок 3.5), через
которую линии уровня входят
в область (точка наименьшего значения
функции) и точку, через которую линии
уровня выходят
из области (точку наибольшего значения
функции).
Пример 3.6
Найти наибольшее
и наименьшее значения функции
![]() в области Q
=
в области Q
=
![]() .
.
Решение. Данная функция – линейная, поэтому, учитывая замечание, воспользуемся графическим методом решения задачи.
Построим область
Q.
Множество точек плоскости, координаты
которых удовлетворяют неравенству
![]() ,
расположены между прямой
,
расположены между прямой
![]() и параболой
и параболой
![]() (рисунок 3.6, а)
(рисунок 3.6, а)
Линии уровня данной
функции имеют уравнение
![]() .
Построим одну из них, например, при
.
Построим одну из них, например, при
![]() ,
т.е. прямую l
с уравнением
,
т.е. прямую l
с уравнением
![]() (рисунок 3.6, б).
(рисунок 3.6, б).
Найдем и построим
вектор
![]() .
Имеем
.
Имеем
![]() ,
,
![]() ,
,
о ткуда
ткуда
![]() .
Для линейной функции градиент не зависит
от точки приложения, поэтому удобно
построить его исходящим из начала
координат (рисунок 3.6, б).
.
Для линейной функции градиент не зависит
от точки приложения, поэтому удобно
построить его исходящим из начала
координат (рисунок 3.6, б).
Передвигая прямую l в направлении градиента, видим, что точкой «входа» в область линий уровня является точка А, а точкой «выхода» – точка В. Координаты точки В находим из пересечения линий границы:

![]()
![]()
![]() .
.
Очевидно, в точке
В
![]() ,
тогда
,
тогда
![]() .
Итак, функция достигает наибольшего
значения в точке В
.
Итак, функция достигает наибольшего
значения в точке В![]() ,
а наибольшее значение равно
,
а наибольшее значение равно
![]() .
.
Найдем координаты
точки А. Эта точка является точкой
касания прямой
![]() и границы
и границы
![]() .
Значит, в этой точке совпадают угловые
коэффициенты этой прямой и касательной
к кривой
.
Значит, в этой точке совпадают угловые
коэффициенты этой прямой и касательной
к кривой
![]() .
Угловой коэффициент прямой
.
Угловой коэффициент прямой
![]() ,
или
,
или
![]() равен
равен
![]() .
Касательная к линии
.
Касательная к линии
![]() в каждой точке х
имеет угловой коэффициент
в каждой точке х
имеет угловой коэффициент
![]() .
Тогда из равенства этих коэффициентов
находим
.
Тогда из равенства этих коэффициентов
находим
![]()
![]()
![]() .
.
Значит, абсцисса
точки А
![]() ,
тогда ордината равна
,
тогда ордината равна
![]() .
Таким образом, данная функция достигает
наименьшего значения в точке А
.
Таким образом, данная функция достигает
наименьшего значения в точке А![]() и это значение равно
и это значение равно
![]() .
.
К отысканию наибольшего (наименьшего) значения функция в области часто приводит решение различных производственных задач. Рассмотрим один из наиболее простых классов таких задач – задачи линейного программирования. Под условным названием «Линейное программирование» понимают задачи на условный экстремум функции нескольких переменных, где и сама функция, и все ограничения, налагаемые на её переменные, линейны относительно этих переменных.
Прежде чем решать задачу производственного характера, относящуюся к задачам линейного программирования, необходимо сформулировать её на математическом языке, или, как говорят, составить математическую модель этой задачи.
Построение математической модели состоит из следующих этапов.
1. Выбрать и обозначить искомые переменные.
2. Составить условия, которым должны удовлетворять эти переменные. Они могут быть записаны в виде равенств или неравенств.
3. Составить функцию
![]() ,
экстремум которой необходимо найти.
Эту функцию называют
целевой
функцией.
,
экстремум которой необходимо найти.
Эту функцию называют
целевой
функцией.
Тогда математическая
постановка рассматриваемой задачи
сводится к следующему: найти наибольшее
(наименьшее) значение функции
![]() ,переменные
которой удовлетворяют условиям:
,переменные
которой удовлетворяют условиям:
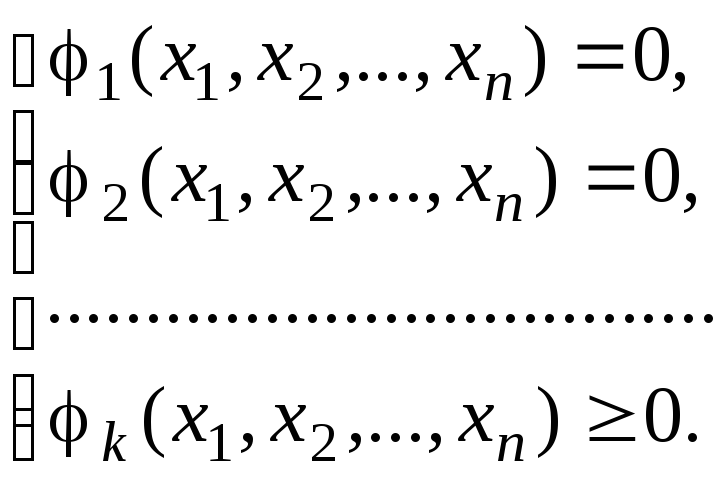
Если задача содержит только две переменные, то её можно решить графическим методом по образу примера 3.6.
