Пример 3.1

Найти экстремум функции .

Решение. При отыскании экстремума функции двух переменных рекомендуем придерживаться следующего алгоритма.

1. Найти область определения функции .

2. Найти критические точки функции, т.е. точки, в которых , или эти производные не существуют (необходимые условия экстремума).

3. Найти частные производные второго порядка от заданной функции и составить .

4. В каждой критической точке вычислить значение ., проверить выполнение достаточных условий экстремума, и сделать вывод, например, используя таблицу:

Условия		Наличие и вид экстремума
		Точка минимума
		Точка максимума
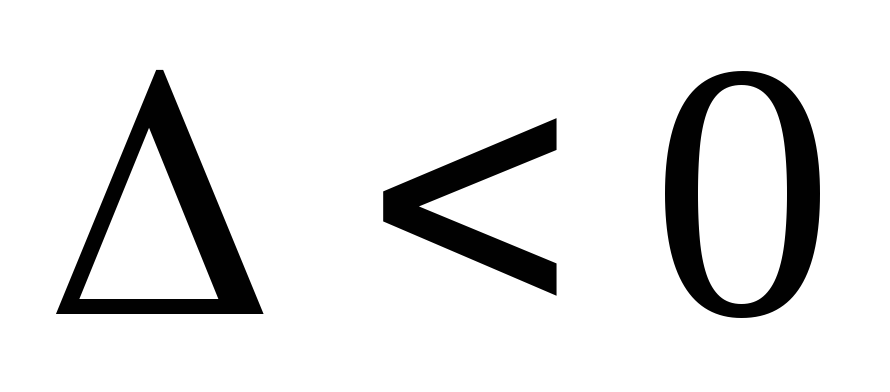
	–	Нет экстремума
	–	Нужны дополнительные исследования

5. Вычислить и/или в найденных точках экстремума.

Используем этот алгоритм в рассмотренной задаче. Область определения функции есть вся плоскость ХОУ.

Найдем частные производные первого порядка:

,

.

Используем необходимые условия экстремума. Так как частные производные определены (существуют) для любых значений х и у, то критические точки найдем из условия равенства нулю частных производных первого порядка, т.е. решив систему уравнений

или

Выразим из первого уравнения , подставим это значение у во второе уравнение, получим

, ,

откуда либо , либо . При получим , а при имеем . Таким образом, получили две критические точки: и .

Найдем частные производные второго порядка

,

,

.

Составим .

Проверим выполнение достаточных условий экстремума для каждой из критических точек и .

а) В точке имеем

,

значит, точка не является точкой экстремума данной функции.

б) В точке получим

,

следовательно, в точке заданная функция имеет экстремум. Чтобы определить, минимум это или максимум, вычислим в точке М₂ значение производной :

,

значит, точка является точкой минимума данной функции. Вычислим значение функции в этой точке

.

Итак, заданная функция достигает экстремума в точке и этот экстремум – минимум, равный (–1).

Пример 3.2

Найти экстремум функции при условии .

Решение. Уравнение связи есть линейное уравнение относительно переменных х и у, из которого легко выразить одну переменную через другую, поэтому будем искать условный экстремум данной функции методом исключения.

Из уравнения выразим и подставим это значение у в функцию , получим функцию одной переменной:

,

,

.

Найдем экстремумы полученной функции. Область определения этой функции . Находим критические точки:

  

.

Проверим наличие экстремума в этих точках (смена знака производной при переходе через эти точки):

Из рисунка 3.1. видно, что в точке функция имеет максимум, а в точке эта функция имеет минимум, причем

,

.

Но точкам экстремума функции соответствуют точки одноименного условного экстремума исходной функции :

при получаем , откуда имеем точку ;

при получаем , откуда имеем точку .

Таким образом, в точке функция имеет условный максимум

,

а в точке эта функция имеет условный минимум

.