Пример 2.8

Найти полное приращение и полный дифференциал функции в точке , если.

а) ; б) ;

в) .

Оценить погрешность замены полного приращения дифференциалом в каждом из этих случаев.

Решение. Найдем полное приращение и полный дифференциал данной функции в точке М для произвольных значений приращений аргументов.

По определению, полное приращение функции равно

,

тогда в точке , т.е. при получим

.

Полный дифференциал функции в точке М, согласно информации 2.2.4, равен

,

где . Найдем частные производные функции :

, ,

откуда , . Тогда дифференциал данной функции в точке М равен

.

Для вычисления абсолютной погрешности  и относительной погрешности  будем использовать формулы:

, .

Тогда для каждой из заданных в условии задачи пар значений приращений аргументов получим следующие результаты.

а) При имеем

,

(т.к. ).

Отсюда абсолютная погрешность замены полного приращения функции ее дифференциалом будет равна , а относительная погрешность .

б) При имеем

,

Тогда абсолютная погрешность замены полного приращения дифференциалом равна , а относительная погрешность .

в) При получим

,

Тогда абсолютная погрешность замены приращения дифференциалом равна , а относительная погрешность – .

Замечание. Если сравнить величины погрешностей  и  соответственно в каждом из случаем а) – в), то можно установить, что они уменьшаются с уменьшением приращений . Это подтверждает тот факт, что при достаточно малых приращениях аргументов выполняется приближенное равенство , поэтому полное приращение можно приближенно заменять дифференциалом. Этот прием широко используется в приближенных вычислениях.

Пусть некоторая величина z является функцией двух переменных х и у: . Определяя каким-либо образом (приближенные) значения величин и , мы допускаем погрешности и , т.е. истинные значения х и у соответственно равны и . Тогда значение величины , вычисленное по приближенным значениям х₀ и у₀ аргументов, получается с погрешностью

.

Как оценить величину этой погрешности, если известны погрешности и аргументов?

Так как для малых справедливо приближенное равенство, то , откуда

.

Величину называют максимальной абсолютной погрешностью, а величину – максимальной относительной погрешностью, которую обычно выражают в процентах.

Пример 2.9

Вычислить приближенно , исходя из значения функции в точке . Оценить абсолютную и относительную погрешность такого приближения..

Решение. Искомое значение будем рассматривать как значение функции в точке с координатами , где ,,,. Воспользуемся приближенным равенством (информация 2.2.5)

В нашем случае

,

,

,

.

Тогда

.

Максимальная абсолютная погрешность вычислений составляет

,

а максимальная относительная погрешность равна

.

Пример 2.10

Линеаризовать функцию в окрестности заданной точки.

а) , ;

б) , .

Решение. а) Используем формулу линеаризации (2.5) (информация 2.2.5)

.

В нашем случае точка – это точка . тогда

.

Найдем частные производные заданной функции

,

.

Вычислим значения этих производных в точке :

,

.

Тогда по формуле (2.5) имеем

,

или, после преобразований,

,

т.е. трансцендентная функция в окрестности точки может быть заменена приближенно равной ей линейной функцией Вид этой линейной функции можно упростить, если взять , получим

.

б) Аналогично линеаризуем функцию в точке . Заметим только, что в соответствии с последовательностью переменных в определении функции , значения этих переменных в точке В таковы: .

Запишем формулу линеаризации (2.5) в соответствии с обозначением данной функции:

,

где – произвольная точка из окрестности точки .

В нашем случае М₀ – это точка . Находим последовательно:

,

,

,

.

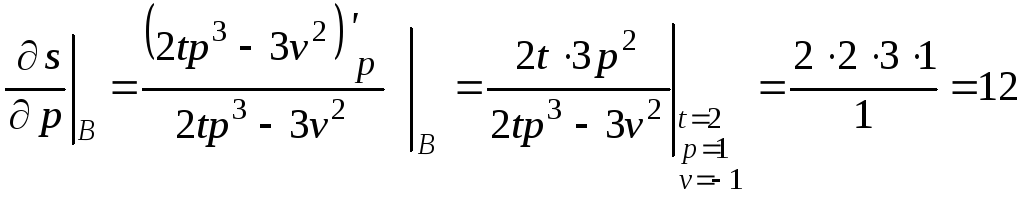Тогда данная функция может быть приближенной заменена линейной так

,

или, после преобразований,

.