2.11 Понятие о гидравлическом и пьезометрическом уклонах

В гидравлике различают гидравлический I и пьезометрический I_P уклоны.

Гидравлическим уклоном называется падение напорной линии на единицу длины. Пусть у нас имеется поток жидкости, показанный на рисунке 2.8. Средний гидравлический уклон для данного потока на участке 1 - 1 и 2 - 2 будет

(2.22)

где - длина участка, для которого определяем гидравлический уклон;

-- потери напора на участке потока длиной .

Если напорная линия криволинейная, гидравлический уклон будет различен в любой точке кривой. Например, гидравлический уклон в точке 1 напорной линии

где ds - элемент длины, на котором произошли элементарные потери напора, равные .

Рисунок 2.8

Падение пьезометрической линии на единицу длины потока называется пьезометрическим уклоном. Средний пьезометрический уклон потока на участке 1 - 2

(2.23)

И если пьезометрическая линия является криволинейной, то пьезометрический уклон в точке 1

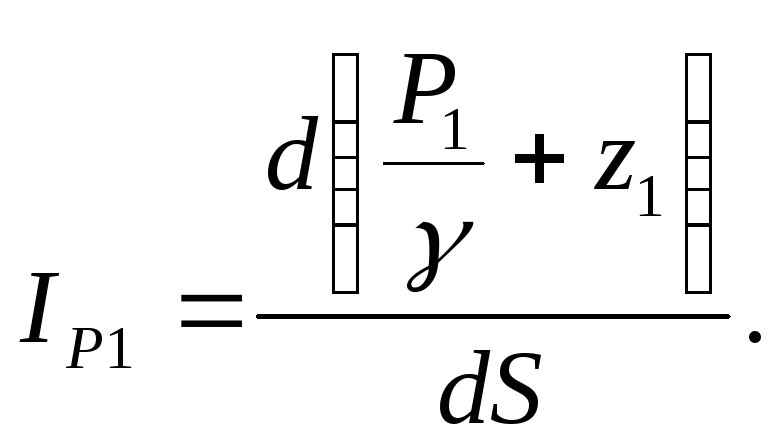
При равномерном движении жидкости гидравлический и пьезометрический уклоны равны между собой, так как при равномерном движении живое сечение и средняя скорость потока постоянны и, следовательно,, тогда

Следует отметить, что пьезометрический уклон может быть или положительным, или отрицательным. Гидравлический уклон всегда будет положительным, так как напорная линия всегда понижается по направлению движения потока, поэтому обратного уклона не может быть.

2.12 Практическое использование уравнения Бернулли

2.12.1 Расходомер Вентури

Практическое применение уравнения Бернулли проиллюстрируем на примере водомера Вентури, применяемого для измерения расхода в водопроводных сетях (рисунок 2.9)

Конструкция водомера следующая. В водопровод вмонтированы два фасонных участка - сходящийся и расходящийся, соединённых между собой трубой (короткой) значительно меньшего диаметра, чем диаметр основного трубопровода.

В сечениях 1 и 2 к водомеру подключены пьезометры, из показаний которых определяется перепад пьезометрического напора на длине конфузора,

Рисунок 2.9

Составим уравнение Бернулли для сечений 1 и 2 (пренебрегая потерями).

Следовательно, разность показаний пьезометров

(2.24)

Из условия сплошности потока

или.

Исключая V₁ из выражения (2.24) и решая относительно V₂,получим

.

Расход, протекающий через водомер.

(2.25)

где С – постоянная водомера.

Величину С можно подсчитать теоретически. Тогда, беря отсчет по показаниям пьезометров и вычисляя , можно по формуле(2.25) определить расход в трубопроводе для любого момента времени. Однако определенный таким образом расход жидкости является теоретическим расходом, так как вследствие неравномерности распределения скоростей в поперечных сечениях потока, а также неизбежных потерь напора между рассматриваемыми сечениями действительный расход жидкости будет несколько отличаться от вычисленного по этой формуле.

Формулу для действительного расхода жидкости, протекающей через водомер Вентури, можно записать в таком виде:

, (2.26)

где - коэффициент расхода водомера, зависящий от его размера, скорости движения и вязкости жидкости; для новых водомеров = 0,985; для водомеров, бывших в употреблении, = 0,98.

Этот коэффициент для каждого расходомера устанавливается путем тарирования, т. е. на основании ряда сравнительных измерений расходов при различных скоростях движения жидкости данным расходомером либо другим способом или прибором (например, объемным или массовым способом).

На практике вместо применения формулы 2.26 расход жидкости определяют с помощью водомера Вентури по так называемым тарировочным кривым полученным опытным путем и дающим для данного водомера непосредственную зависимость между и измеряемым расходом жидкостиQ.