1.12 Давление жидкости на плоскую горизонтальную поверхность. Гидростатический парадокс

Имеем сосуд (рисунок 1.15,а). Глубина воды в сосуде h. Давление жидкости в какой-либо точке сосуда зависит от глубины погружения этой точки. Если взять точкиА,БиС, то давления в них соответственно будут равны

р_А=γ·h_A;р_Б=γ·h_Б;р_С=γ·h_С.

Сила суммарного давления на горизонтальную площадку

F_c=γ·h_c·ω.

Суммарное же давление на все дно сосуда площадью Ω может быть определено по формуле

Р=γ·h·Ω. (1.51)

Следовательно, суммарная сила давления жидкости на горизонтальную поверхность равна весу столба жидкости, расположенного над рассматриваемой поверхностью.

На рисунке 1.15,б изображены три сосуда различной формы. Площадь дна всех сосудов одинакова Ω. Все сосуды наполнены однородной жидкостью на глубину Н. Гидростатическое давление на дно во всех сосудах будет одинаковым и равнымр=γ·Н.

С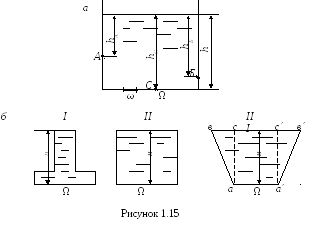уммарное гидростатическое давление на дно любого из трех показанных на рис. 1.15,б сосудов будет также одинаковым и равнымР=р·Ω=γ·Н·Ω. Спрашивается, откуда берется в сосудеIдополнительная сила по сравнению с сосудомIIи куда пропадает избыток веса жидкости в сосудеIIIпо сравнению с сосудомII? Нет ли здесь противоречия с законами физики?

Законы гидравлики утверждают, что давление жидкости не зависит от формы сосуда, а зависит от глубины погружения площади и ее размеров. В этом и состоит гидростатический парадокс. На поставленные вопросы дают объяснение особые свойства жидкости передавать внешнее давление по всем направлениям и с одинаковой силой (закон Паскаля). Например, на дно сосудаIIIдействует суммарное гидростатическое давлениеР=γ·Н·Ω. Что касается жидкости, находящейся в объемахавсиа´в´с´, то ее вес воспринимается наклонными стенками, а не дном сосуда. Безусловно, если сосудIIIбудет стоять на столе, то стол воспринимает вес всей жидкости, находящейся в сосуде. Следовательно, никакого противоречия между законами физики и гидравлики не существует. Суммарное гидростатическое давление на дно сосуда зависит от глубины погружения и площади и не зависит от формы сосуда.

1.13 Сила давления жидкости на криволинейные поверхности

При определении результирующей силы давления покоящейся жидкости на криволинейную поверхность следует иметь ввиду, что если при определении силы действующей на плоскую поверхность мы имеем дело с элементарными силами, действующими по нормали к ней и параллельно друг другу, то для криволинейной поверхности эта параллельность элементарных сил в разных ее точках не имеет места (рисунок 1.16). В связи с этим непосредственное определение результирующей силы давления жидкости на криволинейную поверхность в общем случае весьма затруднительно. Поэтому обычно вначале определяют три составляющие силы F, а затем геометрически складывают их. Чаще в качестве составляющих берут проекции на координаты оси и тогда результирующая сила Р определится как

F=.

В отдельных случаях элементарные силы давления на криволинейные поверхности могут приводится к одной равнодействующей силы. Так, например, для части шаровой поверхности элементарные силы давления будут направлены по радиусам, пересекутся в центре сферы, и дадут одну равнодействующую силу. Точно также к одной силе сведутся элементарные силы давления жидкости на цилиндрические поверхности.

Определим силу давления жидкости на криволинейную цилиндрическую поверхность.

Рассмотрим два случая.

Первый – жидкость находится над криволинейной поверхностью (рисунок 1.17). На криволинейной поверхности выделим бесконечно малую площадку dS, центр тяжести которой погружен на глубинуh.

Элементарная сила давления направлена по нормали к площадке

.

Разложим эту силу на вертикальную

;

.

Выражения cosα·dS иsinα·dSпредставляют собой площади проекций бесконечно малой площадкиdSна горизонтальную вертикальную плоскости, т.е.xoy иyoz. Тогда

;

.

Представим, что вся поверхность фигуры, равная S, состоит из бесконечно малых площадокdS, на каждую из которых действуют составляющие элементарных сил гидростатического давленияdF_zиdF_x:

;

.

Интеграл представляет собой объем воображаемого жидкого тела, ограниченного снизу криволинейной поверхностьюS, а сверху ее проекциейS_xна плоскость свободной поверхности жидкости. Полученное таким образом воображаемое жидкое тело называется телом давления.

Следовательно, вертикальная составляющая силы F_zчисленно равна весу жидкости в объеме тела давления

, (1.52)

где - объем тела давления.

Вертикальная составляющая F_zпроходит через центр тяжести тела давления. Направление ее (вверх или вниз) определяется взаимным расположением жидкости и криволинейной поверхности. Если тело давления образовано жидкостью (положительное тело), то вертикальная составляющаяF_zнаправлена вниз (рисунок 1.17), если же это тело лежит со стороны, противоположной жидкости (отрицательное тело давления), тоF_zнаправлено вверх (рисунок 1.18).

Для горизонтальной составляющей интеграл является статическим моментом площади проекции криволинейной фигуры на вертикальную плоскостьyoz.

Из курса теоретической механики следует, что статический момент равен произведению проекции криволинейной поверхности на глубину погружения центра тяжести проекции криволинейной поверхности.

Тогда горизонтальная составляющая силы

, (1.53)

где S_z– площадь проекции криволинейной фигуры на плоскостьyoz;

h_ц..т– глубина погружения центра тяжести площади проекции под пьезометрическую плоскость.

Таким образом, горизонтальная составляющая силы F_x– произведение площади проекции криволинейной фигуры на вертикальную плоскость на гидростатическое давление в центре тяжести этой площади.

Полную силу давления Fнаходят как равнодействующую горизонтальной и вертикальной составляющих

F=. (1.54)

Направление силы суммарного давления Fопределяется углом ее наклона к горизонту, т.е. углом

. (1.55)

Отметим, что центр давления, т.е. точка приложения силы давления жидкости, может быть найдена графическим путем как точка пересечения направления силы Fс криволинейной поверхностью.