Логические элементы и таблица истинности

В основе всех цифровых систем лежат четыре основных логических элемента (операций):

1. Логическое сложение, дизъюнкция, ИЛИ

2. Логическое умножение, конъюнкция, И

3. ИЛИ - исключающее

4. Отрицание, НЕ

Все эти элементы обладают свойством функциональной полноты, т.е. на их основе может быть решена любая логическая непротиворечивая функция.

В электротехнических системах логические элементы принято обозначать в виде прямоугольников со сторонами кратным 5 мм, причем, слева показаны входы, справа выходы.

Входные величины по правилам алгебры логики обозначаются, как правило, заглавными латинскими буквами (A,B,C…), так же обозначаются и выходные переменные. Связь между входами и выходами определяется конкретной логической функцией.

Одним из основных инструментов для анализа цифровых комбинационных схем на этих элементах является таблица истинности, которая состоит из N– столбцов, гдеN– 1 равно количеству входных переменных. А последний столбец принимает значение выходной переменной. Если количество входных переменных равноK, то количество строк в этой таблице равно 2^K. Важной особенностью всех входных и выходных переменных в алгебре логике является то, что все они могут принимать только два значения – нуля или единицы.

Логическое сложение, дизъюнкция, элемент или

Для обозначения операции ИЛИ в алгебре логике используется символ «+». Например, AилиB=A+B.

Примем, что если ключ A(B) замкнут, то А (В) равно единице, и наоборот, если разомкнут, тоA(B) равно Ø. Если лампочкаQгорит, тоQ=1, если не горит, тоQ=Ø.

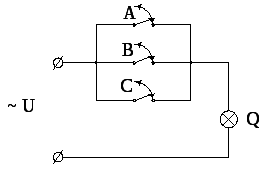
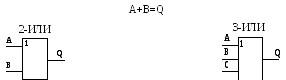Анализ выполним с помощью таблицы истинности. Выходными переменными являются А и В, выходной переменной –Q.

A	B	C	Q
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

A	B	Q
0	0	0
1	0	1
0	1	1
1	1	1

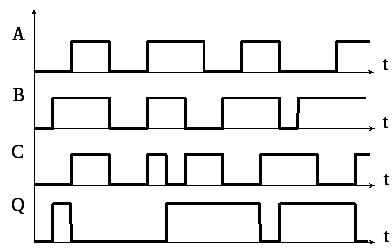
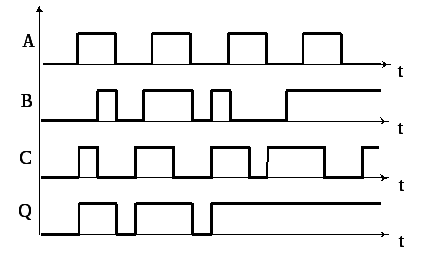
Все физические процессы протекают и исследуются, как правило, во времени, поэтому чтобы знать, когда и как произошло, то или иное событие используются диаграммы состояний.

Логическое умножение, конъюнкция, элемент и

В алгебре логике операция логического умножения обозначается символом умножить «·». Например, А и В =.

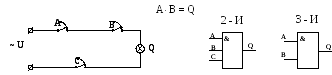
A	B	Q
0	0	0
0	1	0
1	0	0
1	1	1

A	B	C	Q
0	0	0	0
1	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	1	0
1	1	0	0
1	1	1	1

Диаграмма состояний для этой функции изображается так же:

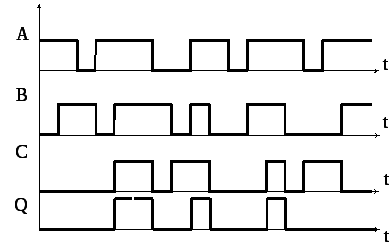
ИЛИ – исключающее

Для обозначения этой операции в алгебре логике используют символ. Например, АВ=Q.

Проиллюстрировать работу этого элемента с помощью ключей и лампочки невозможно, поэтому необходимо знать таблицу истинности.

A	B	Q
0	0	0
0	1	1
1	0	1
1	1	0

A	B	C	Q
0	0	0	0
0	1	1	1
1	0	1	1
1	1	0	1
1	1	1	0