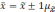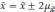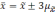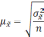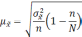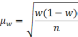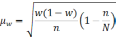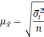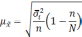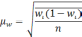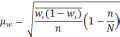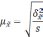- •Тема 1. Предмет, метод и задачи статистики
- •Тема 2. Теория статистического наблюдения
- •1.Понятие статистического наблюдения, его организационные формы
- •2.Виды и способы статистического наблюдения
- •Тема 3. Статистическая сводка и группировка
- •2.Статистические группировки, их виды и задачи
- •3.Этапы построения статистических группировок.
- •4. Статистические таблицы
- •5.Статистические графики.
- •Тема 4. Абсолютные, относительные и средние величины
- •2.Относительные величины, их значение и основные виды
- •4. Сущность и виды средних величин.
- •5. Структурные средние величины
- •Тема 5. Статистическое изучение вариации
- •2. Показатели вариации и способы их расчета
- •3.Виды дисперсий и правила их сложения
- •Тема 6. Выборочное наблюдение
- •3. Понятие ошибки репрезентативности, виды ошибок репрезентативности
- •4. Определение необходимой (оптимальной) численности выборки
- •5. Распространение результатов выборочного наблюдения на генеральную совокупность
- •Тема 7 анализ временных рядов
- •1. Понятие о статистических рядах динамики
- •2. Показатели временных рядов
- •Тема. Экономические индексы
- •2. Индивидуальные и агрегатные индексы
- •3. Средние индексы из индивидуальных (групповых)
- •4. Индексы переменного и фиксированного состава. Индекс структурных сдвигов.
3. Понятие ошибки репрезентативности, виды ошибок репрезентативности
Ошибка репрезентативности - расхождение между выборочной характеристикой и характеристикой генеральной совокупности.
Ошибки репрезентативности
Систематические - возникают в результате нарушения научных принципов отбора единиц совокупности (преднамеренные и непреднамеренные).
Случайные возникают в результате несплошного характера наблюдения (средняя и предельная ошибки выбора).
Случайные ошибки могут быть доведены до незначительных размеров, а главное, их размеры и пределы можно определить с достаточной точностью на основании закона больших чисел.
Средняя ошибка выборки - такое расхождение между средними выборочной и генеральной совокупностями, которое не превышает ±.
В математической статистике доказывается, что значения средней ошибки выборки определяются по формулам:
Формула для определения величины средней ошибки выборки для количественного признака:
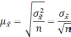
Формула для определения величины средней ошибки выборки для альтернативного признака:

Полученное
значение средней ошибки необходимо для
установления возможного значения 
 .
Которое определяется по формуле:
.
Которое определяется по формуле:
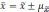
Но такое суждение можно гарантировать не с абсолютной достоверностью, а лишь с определенной степенью вероятности.
В математической статистике доказывается, что пределы значений характеристик генеральной совокупности отличаются от характеристик выборочной совокупности лишь с вероятностью, которая определена числом 0,683.
Это
означает, что в 683 случаях из 1000 генеральная
средняя будет находиться в установленных
пределах, т.е. отклонение ГС от ВС не
превысит однократной средней ошибки
выборки. В остальных 317 случаях они могут
выйти за эти пределы. Вероятность можно
повысить, если расширить пределы
отклонений. Так, при удвоенном значении

 ,
вероятность достигает 0,954 (
,
вероятность достигает 0,954 (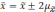
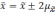 ).
Если утроить значение то вероятность
увеличится до 0,997 (
).
Если утроить значение то вероятность
увеличится до 0,997 (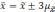
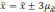 ).
).
|
Возможное значение генеральной средней |
Вероятность |
|
|
0,683 |
|
|
0,954 |
|
|
0,997 |
Если
обозначить значение увеличения 
 за
t,
то можно записать в общем виде:
за
t,
то можно записать в общем виде:
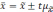
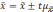
Множитель t называется коэффициентом доверия. Известный русский математик А.М.Ляпунов дал выражение конкретных значений множителя t для различных степеней вероятности в виде функции:
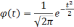
На практике пользуются готовыми таблицами этой функции.
|
t |
0 |
0,1 |
0,5 |
1 |
1,5 |
2 |
2,5 |
2,6 |
3 |
4 |
|
(t) |
0,1 |
0,0797 |
0,3829 |
0,6827 |
0,8664 |
0,9545 |
0,9876 |
0,9907 |
0,9973 |
0,99994 |
Из
вышесказанного следует, что лишь с
определенной степенью вероятности
можно утверждать, что показатели
генеральной совокупности и их отклонения
не превысят величину 
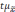 .
Полученную величину
.
Полученную величину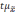
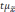 называетсяпредельной
ошибкой выборки.
называетсяпредельной
ошибкой выборки.
Предельная ошибка выборки - максимально возможное расхождение выборочной и генеральной средних, т.е. максимум ошибки при заданной вероятности ее появления.
Предельная ошибка выборки для количественного признака:
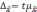
Предельная ошибка выборки для альтернативного признака:
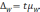
В связи с тем, что существуют различные методы, виды и способы отбора единиц из генеральной совокупности формулы для расчета средней ошибки выборки также будут различаться:
|
Способ отбора |
Оцениваемый параметр |
Повторный отбор |
Бесповторный отбор |
|
Собственно случайный и механический |
Средняя |
|
|
|
Доля |
|
| |
|
Типический |
Средняя |
|
|
|
Доля |
|
| |
|
Серийный |
Средняя |
|
|
|
Доля |
|
|
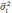
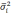 - средняя из групповых дисперсий;
- средняя из групповых дисперсий;
wi - доля единиц совокупности, обладающих изучаемым признаком в i-й типической группе;
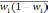
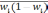 - средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;
- средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;
S – общее число серий;
s – число отобранных серий;

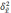 -
межгрупповая дисперсия средних,
определяемая по формуле:
-
межгрупповая дисперсия средних,
определяемая по формуле:
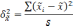
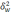
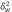 -
межгрупповая дисперсия доли, определяемая
по формуле:
-
межгрупповая дисперсия доли, определяемая
по формуле:
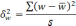
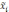
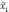 - средняя
i-й
серии;
- средняя
i-й
серии;

 -
средняя по всей выборочной совокупности;
-
средняя по всей выборочной совокупности;
w - доля признака i-й серии;

 - общая доля признака во всей выборочной
совокупности.
- общая доля признака во всей выборочной
совокупности.