
- •Оглавление.
- •I. Введение.
- •II.Н. И. Лобачевский и его геометрия.
- •III. Пятый постулат Евклида.
- •IV. Система аксиом Гильберта.
- •Группа 1. Аксиомы принадлежности.
- •ГруппаIi.Аксиомыпорядка.
- •ГруппаIii.Аксиомыконгруэнтности.
- •Группа IV. Аксиомы непрерывности.
- •Группа V. Аксиома параллельности.
- •V. Аксиома Лобачевского. Параллельные прямые по Лобачевскому.
- •VI. Теорема о существовании параллельных прямых.
- •VII. Треугольники и четырехугольники на плоскости Лобачевского.
- •VIII. Взаимное расположение двух прямых на плоскости Лобачевского.
- •IX. Три модели геометрии Лобачевского.
- •1) Модель Пуанкаре.
- •2) Модель Клейна.
- •3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)
- •X. Практическое применение геометрии Лобачевского.
- •1) Теорема Пифагора.
- •3) Площадь треугольника
- •4) Длина окружности и площадь круга.
- •XI. Вывод.
- •XII. Литература.
III. Пятый постулат Евклида.
Евклид так определяет параллельные прямые: две прямые называются параллельными, если они лежат в одной плоскости и не имеют общей точки.
Лемма 1. Если при пересечении двух прямых секущей накрест (лежащие углы (или соответственные углы) равны, то прямые не пересекаются.
□ Пусть
при пересечении прямых а
и b
секущей АВ
накрест
лежащие углы равны (например,
![]() 1
=
1
=![]() 2
на рис. 206). Если допустить, что прямыеа и
b
пересекаются
в некоторой точке Р, то получим
треугольник АВР,
у которого
один из углов при вершине А
или В
равен внешнему
углу при другой вершине (см. рис.).
2
на рис. 206). Если допустить, что прямыеа и
b
пересекаются
в некоторой точке Р, то получим
треугольник АВР,
у которого
один из углов при вершине А
или В
равен внешнему
углу при другой вершине (см. рис.).

Но это противоречит теореме о внешнем угле треугольника. Второе утверждение теоремы непосредственно следует из доказанного. Чтд.
Возникает вопрос: сколько же через точку М, не лежащую на прямой а, проходит прямых, параллельных прямой а? Ответ на него дает следующая теорема.
Теорема 1. Если имеет место V постулат, то через каждую точку М, не лежащую на прямой а, проходит только одна прямая, параллельная прямой а.
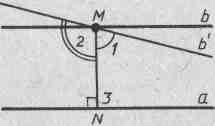
![]() а, и прямую b,
проходящую через точку
М перпендикулярно
к прямой MN
(см. рис ниже). Тогда прямые
а и b
параллельны.
а, и прямую b,
проходящую через точку
М перпендикулярно
к прямой MN
(см. рис ниже). Тогда прямые
а и b
параллельны.
Проведем
через точку М
произвольную
прямую b’
отличную от
прямой b.
Один из
смежных углов 1 либо 2, отмеченных на
этом же рисунке , острый; пусть
![]() 1
острый. При пересечении прямыха
и b'
с прямой MN
получаем
внутренние односторонние углы:
1
острый. При пересечении прямыха
и b'
с прямой MN
получаем
внутренние односторонние углы:
![]() 1
и
1
и![]() 3,
сумма которых меньше
двух прямых углов, значит, по V
постулату
прямые а и
b'
пересекаются.
■
3,
сумма которых меньше
двух прямых углов, значит, по V
постулату
прямые а и
b'
пересекаются.
■
Существует и обратная теорема:
Теорема 2. Если принять, что через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной, то справедлив V постулат.
Итак, V постулат эквивалентен (равносилен) так называемой аксиоме параллельных прямых: через точку, не лежащую на данной прямой, проходит не более чем одна прямая, параллельная данной.
Лемма
2. Для
произвольного треугольника ABC
можно построить
треугольник А1В1С1
так, чтобы
![]() АВС
=
АВС
=![]() А1В1С1
и
А1
А1В1С1
и
А1![]()
![]()
Теорема 4. Сумма углов любого треугольника не больше 2d.
□ Теорему
докажем методом от противного. Пусть
существует треугольник
ABC,
такой,
что
![]() АВС
= 2d +
АВС
= 2d +
![]() ,
где
,
где![]() >
0. Применяяпредыдущую
лемму к треугольнику ABC
n
раз, построим
треугольник АпВпСп,
удовлетворяющий
условиям
>
0. Применяяпредыдущую
лемму к треугольнику ABC
n
раз, построим
треугольник АпВпСп,
удовлетворяющий
условиям
![]() АпВпСп
=
АпВпСп
=
![]() АВС
и Аn
АВС
и Аn
![]()
![]() А.
А.
![]() Выберем
п так,
чтобы 1/2n
А<
Выберем
п так,
чтобы 1/2n
А<
![]() . Тогда Ап
<
. Тогда Ап
<
![]() .
Так как Аn
+ Вn
+ Сп
= 2d +
.
Так как Аn
+ Вn
+ Сп
= 2d +
![]() ,
то Вп
+ Сп>
2d.
,
то Вп
+ Сп>
2d.
С
другой стороны, легко доказать, что Вп
+ Сп
< 2d. В самом
деле, если
![]() - мера внешнего угла треугольникаАпВпСп,
смежного с
углом Вп,
то
- мера внешнего угла треугольникаАпВпСп,
смежного с
углом Вп,
то
![]() >Сп,
а по теореме
о смежных углах
>Сп,
а по теореме
о смежных углах
![]() +Вп
= 2d, поэтому
Вп
+
Cn
<С
2d.
Мы
пришли к противоречию, следовательно,
не существует
такого треугольника ABC,
сумма углов
которого больше чем 2d.
Чтд.
+Вп
= 2d, поэтому
Вп
+
Cn
<С
2d.
Мы
пришли к противоречию, следовательно,
не существует
такого треугольника ABC,
сумма углов
которого больше чем 2d.
Чтд.
Итак, сумма углов любого треугольника не больше 2d. Но не может ли получиться так, что у одних треугольников эта сумма меньше 2d, а у других равна 2d? Отрицательный ответ на этот вопрос дает вторая теорема Саккери — Лежандра.
Теорема 5. Если в одном треугольнике сумма углов равна 2d, то сумма углов любого треугольника равна 2d. \
Итак получаем еще одно предположение, эквивалентное V постулату: существует хотя бы один треугольник, сумма углов которого равна 2d.
