
глава2
.pdf
2. ПОДХОДЫ К МОДЕЛИРОВАНИЮ ЭЛЕМЕНТОВ ОБОГАТИТЕЛЬНОЙ ТЕХНОЛОГИИ
2.1. Состав продуктов и расчет показателей обогащения
2.1.1. Характеристики крупности
При аналитическом моделировании процессов обогатительной технологии идеализируется такой основной элемент структуры продуктов обогащения, как кусок или частица.
Реальная частица обычно бывает неправильной формы. Модельное представление куска состоит в замене куска случайной формы на кусок эквивалентный ему по какой-либо заданной характеристике. Известны представления частиц в виде куба, цилиндра, диска, конуса и т. п., самым распространенным является использование в качестве эквивалентной частицы шара.
Эквивалентность частицы неправильной формы шару (сфере) по Аллену позволяет ввести различные эквивалентные диаметры частиц:
− поверхностный диаметр dS – диаметр шара с площадью поверхности, равной площади поверхности частицы Sч:
dS |
= |
Sч ; |
|
|
π |
− объемный диаметр dV – диаметр шара, объем которого равен объему |
||
частицы Vч: |
|
6Vч ; |
dV |
= 3 |
|
|
|
π |
− диаметр площади проекции da – диаметр шара, проекция которого имеет площадь, равную площади проекции частицы Sa:
dа =  4SπA ;
4SπA ;
− диаметр периметра проекции dP – диаметр шара, длина окружности проекции которого равна периметру проекции частицы Р:
dP = Р/π;
−диаметр торможения dd – диаметр шара, лобовое сопротивление которого равно лобовому сопротивлению частицы при движении с одинаковой скоростью в жидкости с одинаковой вязкостью;
−диаметр свободного падения df, – диаметр шара, плотность и скорость свободного падения которого в среде одинаковой плотности и вязкости те же, что и у частицы;
−диаметр Стокса dSt – диаметр свободного падения в ламинарном потоке
(Re = 0,2):
d 3 dSt = dV ;
d
1
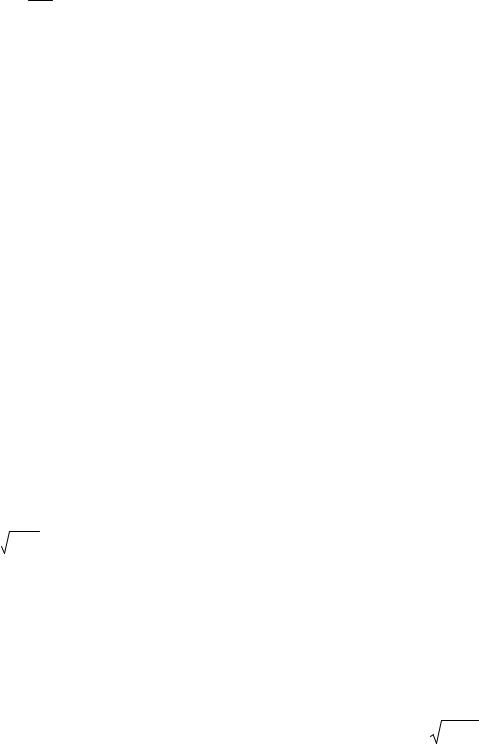
−ситовый диаметр dA – размер минимального квадратного отверстия, через которое проходит частица;
−диаметр удельной объемной поверхности dVS – диаметр шара, имеющего то же отношение площади поверхности к объему, что и частица:
d 3
dVS = dV2 .
S
Методом измерения крупности обычно определяется вид получаемой характеристики. Так, при ситовом анализе результат представляют в виде ситового диаметра dA, при седиментационном – в виде диаметра Стокса dSt, при наблюдении под микроскопом могут получиться поверхностный диаметр dS или диаметр периметра проекции df, площади проекции da и т. д.
При моделировании некоторых сходных процессов не всегда удается анализировать гранулометрический состав одинаковыми методами, а потому для сопоставления процессов необходимо соотнесение между собой различным образом выраженных эквивалентных сферических диаметров. Отношение любой пары вышеуказанных диаметров остается постоянным в широком диапазоне крупности частиц любого материала. Благодаря этому результаты, полу-
ченные разными методами измерений, обычно хорошо коррелированы между
собой.
При возможности непосредственного измерения размеров кусков и бли-
зости их по форме к параллелепипеду с длиной l, шириной b и толщиной h размер оценивают некоторым «средним арифметическим диаметром»:
dср = l + b + h . 3
Заметим, что такая оценка по сути характеризует средний линейный размер куска и не приводит кусок к шару.
К понятиям «средний диаметр», оценивающим крупность частиц неправильной формы одним линейным размером, относится и «средний геометрический диаметр»:
dг = 3 l b h.
Здесь полагается, что близкая по форме к параллелепипеду частица заменяется кубом с ребром dг.
Множественность понятий эквивалентного и среднего диаметра частицы требует всякий раз оговаривать, какая характеристика положена в основу эквивалентности или каким образом достигнуто усреднение.
Для узкого класса крупности, ограниченного пределами d1 и d2, средний диаметр частиц определяют по формулам:
арифметический: |
d |
ср |
= |
d1 + d2 |
; |
геометрический: |
d |
г |
= |
d d |
2 |
; |
|
||||||
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4d 5 |
− d 5 |
||||
гармонический: |
|
|
|
|
2d d |
2 |
|
|
по форме: |
|
|
|
|||||||
d |
Н |
= |
|
|
1 |
; |
d |
Н |
= |
1 |
|
|
2 |
. |
|||||
d |
+ d |
|
5d 4 |
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
− d 4 |
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
||
Весь продукт, состоящий из смеси частиц разной крупности, входящих в различные узкие классы крупности, С. Е. Андреев предложил характеризовать
2

средним диаметром по следующим формулам:
средний диаметр продукта
|
n |
арифметический по массе |
dам = ∑ γi di |
частиц(средневзвешенный): |
i=1 |
|
n |
арифметический по числу частиц: |
dач = ∑ γi di−2 |
|
i=1 |
n
∑ γi ;
i=1
n
∑ γi di−3 ; i=1
гармонический по выходу (средневзвешенный по удельной поверхности):
гармонический по числу частиц (при эквивалентности средней удельной поверхности):
геометрический по числу частиц (в логарифмической форм):
геометрический по выходам:
n |
n |
|
dнв = ∑ γi |
∑ γi di−1 ; |
|
i=1 |
i=1 |
|
n |
|
n |
dнч = ∑ γi di−3 |
∑ γi di−4 ; |
|
i=1 |
|
i=1 |
n |
|
n |
lg dгч = ∑ |
γi di−3 |
lg di ∑ γi di−3 ; |
i=1 |
|
i=1 |
n |
|
n |
lg dгм = ∑ γi lg di ∑ γi . |
||
i=1 |
|
i=1 |
Здесь γi – выход узкого i-го класса крупности; di – диаметр, принимаемый за средний для i -го класса крупности; Σ γi – суммарный выход всех классов.
Чаще других в обогащении используется понятие средневзвешенного диаметра.
Числовая характеристика гранулометрического состава удобна в использовании, но недостаточно информативна. Можно привести простые примеры, когда продукты с одинаковыми значениями средних диаметров или с равными содержаниями минусового класса по контрольному ситу имеют совершенно различный диапазон изменения крупности, преобладание крупных частиц в одних продуктах и мелких в других (рис. 2.1).
w(d) |
а |
R – (d) |
б |
|
|
|
|
||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
R – (dА) |
А |
|
|
2 |
3 |
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
dср |
d |
dА |
d |
Рис. 2.1. Представление гранулометрического состава одним числом:
а – среднеарифметическим по массе частиц (1 – узкий класс, полученный на двух ситах, 2, 3 – классы, полученные на одном сите); б – содержанием минусового класса на контрольном сите (1, 2 – соответственно широкий и узкий диапазон крупности частиц)
3
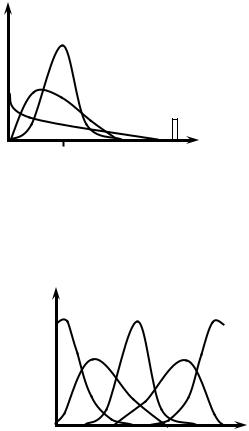
Поэтому при необходимости охарактеризовать гранулометрический состав более полно используют понятие распределения материала по крупности. Графически их представляют кумулятивными характеристиками и плотностями распределения вероятности (рис. 2.2). Чаще такие распределения получают по массе кусков, реже по числу кусков или суммарной поверхности кусков.
R + (d) |
|
|
а |
|
w(d) |
б |
||||
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
1/dmax |
1 |
|
|
||
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
2 |
|
|
||
|
2 |
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
dmax |
d |
|
dmax d |
|||||
|
|
|
|
|||||||
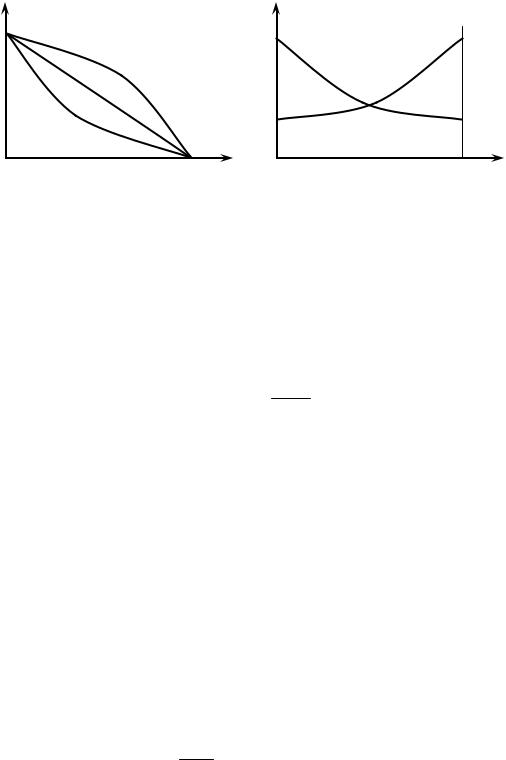
Рис. 2.2. Типичные кумулятивные характеристик надрешетного (плюсового) продукта (а) и соответствующие плотности распределения вероятностей (б)
Простым описанием кумулятивных кривых гранулометрического состава является степенной закон для выхода R – (d), т. е. подрешетного продукта (урав-
нение Годена – Андреева):
R – (d) = (d/dmax)c и R + (d) = 1 – (d/dmax)c,
где d – размер куска, dmax – максимальный размер куска; с – коэффициент. Этому закону соответствует ω(d) распределения вероятности:
= cd c−1 w(d) dmaxc .
При с = 1 (см. рис. 2.2) кумулятивная кривая превращается в прямую линию 1, ей соответствует равномерный закон распределения; при с < 1 кумулятивная кривая для надрешетного продукта имеет вогнутый вид и правоасимметричную плотность распределения вероятностей (кривая 2); при с > 1 кумулятивная кривая для надрешетного продукта имеет выпуклый вид и левоасимметричную плотность распределения вероятностей (кривая 3).
Известны более сложные законы описания гранулометрического состава (подробно рассматриваются в работах Л. П. Шупова). Чаще других используется
уравнение Розина – Раммлера:
R + (d) = exp [-a (d/dmax)c] и R – (d) = 1 – exp [-a (d/dmax)c],
где а и с – коэффициенты, d – текущий размер куска; dmax – максимальный размер куска.
Плотность распределения массы классов по ситовому составу в этом случае хорошо описывается распределением Вейбулла:
d c−1 w(d ) = a c dmaxc
|
|
|
|
d |
c |
|
exp |
|
|
|
|
|
|
|
|
|||||
|
− a |
d |
|
. |
||
|
|
max |
|
|||
|
|
|
|
|||
При изменении численного значения коэффициента с уравнение позволя-
4

ет описывать широкий класс кривых, после простых преобразований линеари-
зуемо, дает хорошую сходимость с |
R + (d) |
R + (d) - R + (dmin) |
|
|||
эмпирическими данными, что обес- |
1 |
|
||||
|
|
|
|
|||
печило ему широкое практическое |
|
|
|
|
|
|
использование. |
R + (dmin) |
R + (dmin) =1 |
|
|||
Формально уравнению Розина |
|
|
|
|
|
|
– Раммлера присущ один недоста- |
R + (d) |
|
|
R + (d - dmin) |
||
ток: R + (d) → 0 только при d → ∞. |
|
|
||||
Поэтому приходится принимать ко- |
|
|
|
|
R + (dmax - dmin) =0 |
|
нечную крупность материала равной |
R + (dmax) |
|
|
|
||
определенному значению выхода |
|
|
|
|
d |
|
класса, что для крупнокусковых |
0 |
dmin |
d |
|||
dmax |
||||||
продуктов приводит к искажению |
Рис. 2.3. Иллюстрация получения усеченного |
|||||
результатов. |
распределения гранулометрического состава |
|||||
Более общее уравнение гранулометрического состава, удовлетворяющее любым граничным размерам фрак-
ций, можно получить на базе уравнения Розина – Раммлера за счет усечения гранулометрической характеристики продукта с параметрами а и с при рассеве продукта на двух ситах (рис. 2.3):
|
|
|
|
− dmin |
c |
|
|
|
|
dmax − dmin |
c |
|
||||||
|
exp |
|
|
d |
|
|
− exp |
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||||||||
|
|
− a |
dmax |
|
|
|
|
− a |
|
|
dmax |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R+ (d) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|||
|
|
|
1 |
− exp |
|
− a |
dmax − dmin |
|
|
|
|
|||||||
|
|
|
|
|
dmax |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где dmin и dmax – размеры отверстий сит, с помощью которых получен продукт с усеченным распределением.
Для полученной системы |
R + (d), % |
|
|
|
|
|
|
|
|||||||||
R + (dmax – dmin) = 0 и |
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
12 |
|
|
|
|
|
|
|
|
||||||||
R + (dmin) = 1, т. е. удовлетво- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13 |
|
|
|
|
|
||||||||||||
ряются краевые условия, дик- |
75 |
|
|
|
|
|
|
|
|
|
[R + (d)]= |
13 |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
туемые физическим |
смыслом |
20 |
|
|
20 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
уравнений крупности. |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При dmin=0 и dmax→ ∞ это |
|
|
|
|
|
|
|
|
25 |
|
|
30 |
|||||
уравнение переходит в обыч- |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ное уравнение Розина – Рамм- |
|
|
|
|
|
|
|
|
30 |
|
|
|
|||||
лера. |
|
12,5 |
|
|
|
|
|
|
|
|
|
d, мм |
|||||
Коэффициенты а, с для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 6,25 25 |
|
50 |
|
|
100 |
||||||||||||
|
|
|
|
||||||||||||||
последнего уравнения могут |
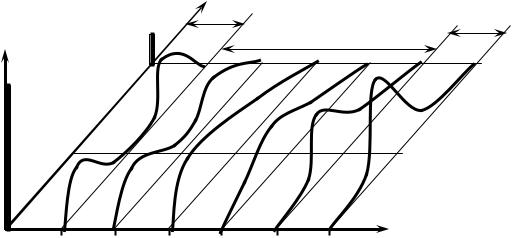
Рис. 2.4. К представлению непрерывного рас- |
||||||||||||||||
быть найдены итерационным |
|||||||||||||||||
пределения |
гранулометрического состава |
||||||||||||||||
методом. |
распреде- |
R + (d) матрицей-столбцом |
|
|
|
||||||||||||
Непрерывное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ление по крупности R + (d) может быть представлено в виде дискретных функций, например, оно может быть заменено на некотором множестве точек d0, d1,
5

d2, ..., dn вектором-столбцом разности значений (рис. 2.4):
R+(d0) – R+(d1); R+(d1) – R+(d2);
…………………
R+(dn-l) – R+(dn) .
При использовании матричного метода желательно постоянство модуля для всей шкалы грохочения. Такой метод хорош тем, что позволяет описывать распределения во всем диапазоне крупности.
Позднее обобщение формул Годена-Андреева и Розина-Раммлера пред-
ложил Свенсен:
R –= Ep[(d/d0)n],
где
|
x |
|
|
|
|
|
|
∫ exp(− z d )dz |
|
|
|
n |
|
|
0 |
|
|
|||
Ep (d ) = |
; |
|
d |
|
|
|
∞ |
|
|
||||
z = |
. |
|||||
|
∫ exp(− z d )dz |
|
d0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
p, который при p=0 |
|
В формуле дополнительно содержится |
параметр |
|||||
обобщает формулу Свенсена в формулу Годена-Андреева, а при p=1 – в формулу Розина –Раммлера. Обычно значения параметров n и p составляют соответ-
ственно 0,5–1,1 и 0,2–1,2.
Экспериментальная проверка формулы Свенсена показала возможность ее применения к очень широкому диапазону гранулометрического состава продуктов дробления. Однако и она не является достаточно общей, неприменима, в частности, для материалов с неплотной структурой, которые легче раскалываются вдоль границ частиц, чем поперек. Для учета этих аномалий предложена формула сочетания двух составов с заданными весовыми коэффициентами t1 и
t1, расширяющая область применения формулы Свенсена:
R –= t1Ep1[(d/d01)]n1+ t2Ep2[(d/d02)]n2.
Эту формулу можно рассматривать как универсальную модель описания гранулометрического состава дробленых продуктов.
Следует заметить, что большое число параметров модели делает ее малоудобной для использования. В определенной степени это относится и к формуле Свенсена. Известны примеры получения моделей гранулометрического состава продуктов дробления-измельчения как частных решений кинетических уравнений разрушения.
2.1.2. Распределение содержаний компонентов в продуктах обогащения
Руды, продукты обогащения состоят из множества кусков самого различного содержания. Распределение содержания в отдельных кусках зависит от их крупности. Раскрытие разных минералов происходит при различной крупности. Если крупность материала достаточна для раскрытия, все куски можно представить мономинеральными и использовать для описания дискретный закон распределения содержания компонента по кускам (рис. 2.5). Если в материале
6

числовая доля кусков минерала равна р, то доля пустой породы: q=1-p.
Такой |
случай |
полностью поддается |
|
|
|
|
аналитическому описанию. Так, массовая до- |
w(α) |
|||||
ля компонента α в продукте: |
w(0)=q |
|
|
|||
|
|
|||||
α = |
nм βм mм |
, |
|
|
|
|
n m + n m |
w(βм)=p |
|
|
|||
|
|
|
|
|||
|
п |
п м м |
|
|
|
|
где nм и nп – число кусков соответственно по- |
|
|
α |
|||
|
|
|||||
лезного минерала и породы; mм и mп – масса |
|
|
βм |
|||
Рис. 2.5. Распределение содер- |
||||||
кусков полезного минерала и породы; βм – |
жания компонента в кусках |
|||||
содержание ценного компонента в минерале; |
полностью раскрытой руды |
|||||
п=пм + пп – общее число кусков. Дисперсия числовой доли:
s2 = p(1− p) .
p n
Здесь р= nм/n.
Дисперсия массовой доли (в дальнейшем покусковая дисперсия) находится по более сложному выражению из-за неравенства масс в общем случае тм и тп. Очевидно, что в случае полного раскрытия покусковая дисперсия всегда больше дисперсии при неполном раскрытии кусков с одинаковым содержанием компонента в материале.
Если допустить, что размер всех кусков одинаков, выражение для α примет вид:
|
|
β |
м |
m m−1 |
|
|
|
β |
m m−1 |
|
|||||
α = |
|
|
|
м п |
|
= |
|
|
м |
|
м |
п |
, |
||
|
nп + nм |
|
mм |
|
|
1 |
|
|
mм |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
+ m |
p |
+ m |
|
|||||||||||
|
|
n |
|
|
− 1 |
|
|
− 1 |
|
||||||
|
|
м |
|
|
|
п |
|
|
|
|
|
|
п |
|
|
а дисперсия массовой доли в соответствии с формулой сложного показателя будет равна:
|
2 |
|
∂α 2 |
|
2 |
|
α4 |
m2 |
|
1 |
|
1 |
|
|
s |
|
= |
|
s |
p |
= |
|
п |
|
|
− 1 |
|
|
. |
|
2 |
|
|
2 |
||||||||||
α |
|
|
|
|
2 |
|
p |
|
|
|
||||
|
|
|
∂p |
|
|
|
βм |
mм |
|
np |
|
|
||
Учитывая, что размер кусков равен d, а плотность минерала и породы со-
ответственно ρм, и ρп, дисперсию массовой доли можно записать: |
|||||||
s2 |
= |
ρм |
α(β |
|
− α) |
[1− α βм + αρп (βмρм)]2 |
. |
ρп |
|
|
|||||
α |
|
|
м |
|
n |
||
а покусковую дисперсию: |
= ρм α(βм − α)[1− α βм + αρп (βмρм)]2. |
||||||
|
smax2 |
||||||
|
|
|
ρп |
|
|
|
|
При сравнительно небольших содержаниях минерала в руде [α≤ (0,05÷0,1)βм] формулу покусковой дисперсии можно использовать в упрощенной форме:
smax2 = ρρм αβм.
п
7
Случай полного раскрытия минералов является гипотетическим (или редко встречающимся, исключение – россыпные руды). В действительности в продуктах обогащения содержатся сростки, и чем больше крупность продукта, тем их доля больше возрастает, причем растет и количество сростков, близких по содержанию к α. Вид распределения при этом видоизменяется и чаще из дискретного эволюционируется в пределе (нераскрытая руда) в нормальный закон
|
α |
Зона |
Зона |
|
дискретного |
||
|
|
закона |
нормального |
|
|
|
закона |
w(α) |
|
|
Переходная зона |
βм |
|
|
αср
0 |
1 |
2 |
3 |
4 |
5 |
6 |
d/dз |
|
Рис. 2.6. Распределение содержания компонента в отдельных кусках с изменением их размера
(рис. 2.6).
С увеличением крупности в отдельных кусках (принимая кубическую модель куска с ребром куба d, с размером зерен определяемого компонента dз, соответствующим крупности раскрытия) отношение d/dз,, постепенно увеличивается. Можно полагать, что в диапазоне от 0 до dз, находится зона дискретного закона, далее следует переходная зона, переходящая в зону нормального закона при больших значениях d/dз. Соотношение d/dз , при котором справедлив нормальный закон, предопределяется конкретными свойствами материала, условиями залегания руды, ее текстурными особенностями, способами добычи и подготовки к обогащению.
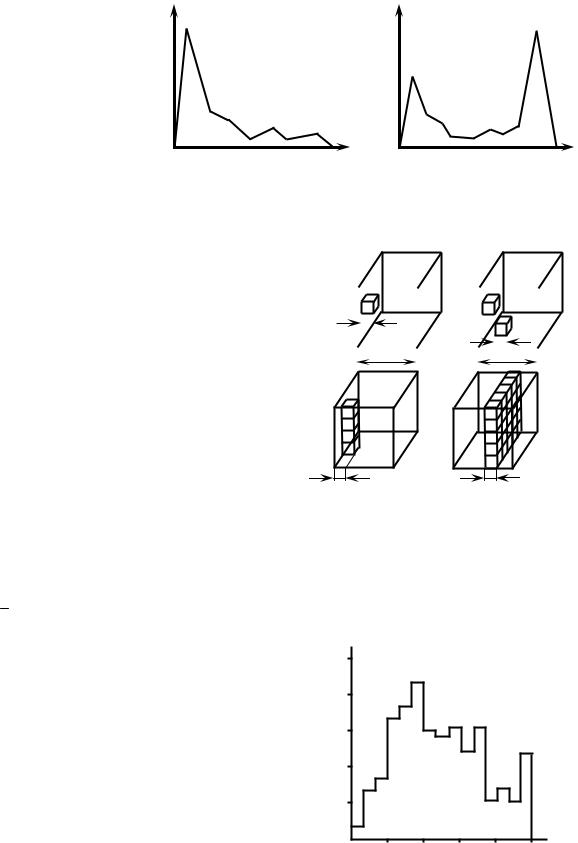
Заметим, что для многокомпонентных руд каждый минерал может иметь различную крупность зерен минералов и, соответственно, разные границы зон законов распределения. Например, для сульфидной медной руды при одной и той же крупности кусков распределения полезных компонентов существенно отличны (рис. 2.7). Так, по меди распределение ближе к зоне нормального, а по сере – дискретного закона, хотя оба несомненно находятся в переходной зоне, по меди распределение – правоасимметричное.
В переходной зоне заметно влияние обычно идеализированно выделяемых текстурных типов руды, и потому можно аналитически проследить взаимосвязь между некоторыми параметрами закона распределения и размерами зерен dз. Однако выбор типа модели руды, а, следовательно, окончательный выбор формул для расчета покусковой дисперсии возможен лишь с использованием специальных экспериментов, позволяющих уточнить некоторые параметры.
8
Для |
пере- |
|
|
p(α), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(α), |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ходной зоны d >dз |
|
|
д. е. |
|
|
|
|
|
|
|
а |
|
|
|
|
|
д. е. |
|
|
|
|
|
|
б |
|
|
|
|
|
|
||||||||||||
поэтому |
|
даже |
|
в |
|
|
|
0,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
самых |
|
богатых |
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
кусках αк< βм. |
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть |
в |
самых |
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
богатых |
|
кусках |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αS, % |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
содержание равно |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
αCu, % |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
10 |
20 |
30 |
40 |
||||||||||||||||||||||||||
αmax. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
неко- |
|
|
|
|
|
|
|
Рис. 2.7. Распределение содержания меди (а) и серы (б) в |
|||||||||||||||||||||||||||||||||
Для |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
торых |
типичных |
|
|
|
|
|
|
|
одних и тех же кусках медноколчеданной руды (p – отно- |
|||||||||||||||||||||||||||||||||
моделей |
|
кусков |
|
|
|
|
|
|
|
сительная частота) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
||||||
(рис. 2.8) ниже |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
приведены общие формулы для вы- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
числения αmax и s2к: |
|
|
ρ |
|
|
|
d 3−b |
|
|
|
|
|
|
|
dз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
αmax = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
м |
|
|
|
|
з |
|
βм; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dз |
|
|
||||||
|
|
ρmax |
|
d 3−b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
в |
|
|
d |
|
|
|
|
|
|
г |
|
d |
|
|
|
|||||||||||||||||||
|
|
s2 |
= |
ρм |
|
dз3−b |
|
|
αβ |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
к |
|
ρ d3−b |
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где b – коэффициент, зависящий от типа руды (b= 0 для равномерно вкрапленных руд; b= 1 для жильных руд; b= 1,5 для вкрапленных руд; b=2 для слоистых руд; b=3 для руд, содержащих всегда раздельные куски ценных компонентов и породы); ρmax – плотность куска с максимальным содержанием полезного компонента;
ρп=ρ для сравнительно бедных руд.
Обычно реальные продукты представлены несколькими текстурами или текстурой с изменяющимися параметрами. Поэтому в конкретных условиях необходимо выполнение экспериментальных работ для определения dз, и b, входящих в формулу покусковой дисперсии.
В зоне нормального закона единственным способом получения распределений содержаний компонентов в кусках является чисто экспериментальный. Для большей части переходной зоны он также предпочтительней, так как дает полную картину распре-
dз |
dз |
Рис. 2.8. Типичные модели кусков:
а – редкая равномерная вкрапленность; б – неравномерная вкрапленность; в – жильное включение; г – слоистое включение
p(α),
д. е 0,15
0,12
0,09
0,06
0,03
0 |
10 |
20 |
30 |
40 |
50 αS, % |
|
Рис. 2.9. Распределение содержания серы в кусках сульфидной медной руды
9
деления, по которой можно определить любые характеристики распределения. Обратную же задачу – получить функцию распределения в целом, вычислив лишь некоторые характеристики распределения, решить невозможно. Примеры экспериментально полученных распределений содержаний компонентов по кускам в переходной зоне приведены на рис. 2.7. Зоне нормального закона, повидимому, близко распределение содержания серы в кусках крупностью -50 +
25 мм сульфидной медной руды одного из месторождений (рис. 2.9). |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Когда известен закон распре- |
|||||||||||||
1 |
|
p(m, nт) |
|
|
|
|
|
|
деления вероятностей |
|
содержаний |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по кускам и предполагается, что их |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
масса постоянна, можно аналитиче- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ски (если распределение оценивается |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формулами) или |
алгоритмически |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
найти закон распределения вероят- |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ностей содержаний по пробам, пре- |
|||||||||||||
|
|
|
αср |
βм αm, n |
восходящим кусок по массе в задан- |
||||||||||||||||||||||||
|
Рис. 2.10. Изменение распределе- |
||||||||||||||||||||||||||||
|
ное число раз. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
ния содержания компонента в |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Например, для случая полного |
||||||||||||||||||||||||||||
|
пробах с увеличением числа кус- |
||||||||||||||||||||||||||||
|
ков nт в них: 1 – 4 при nт соответ- |
раскрытия |
распределение |
числовой |
|||||||||||||||||||||||||
|
ственно равном 1, 10, 100, 1000 |
доли минеральных кусков т в об- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щем числе кусков пробы nт подчиня- |
|||||||||||||
|
|
w(α) |
|
|
|
|
p<<0,5 |
|
|
p>>0,5 |
ется биномиальному закону распре- |
||||||||||||||||||
1 |
|
|
|
|
(p→0) p=0,5 |
|
|
(p→1) |
|
|
деления: |
|
|
|
nт! pm qnт − m |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
p<0,5 |
p>0,5 |
|
|
p (m, nт ) = |
. |
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m!(nт |
− m)! |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Содержание компонента в то- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чечной пробе, состоящей из nт кус- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α/ βм |
ков и содержащей т кусков опреде- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||||
Рис. 2.11. Распределение содержания ком- |
ляемого компонента: |
|
|
|
|
|
|
||||||||||||||||||||||
понента в пробах с изменением числовой |
|
|
|
|
|
|
3 |
|
|
mρмβм |
|
||||||||||||||||||
доли кусков определяемого компонента |
αm,n |
= |
mρмd βм |
= |
. |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
(среднего содержания) при большом и |
т |
|
n |
ρ |
п |
d 3 |
|
n |
ρ |
п |
|||||||||||||||||||
|
|
т |
|
|
|
|
|
т |
|
||||||||||||||||||||
неизменном nт |
|
|
|
|
|
|
В данном случае значение т |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проходит |
весь дискретный ряд чи- |
||||||||||||
сел от 0 до nт.
С увеличением числа кусков nт, попадающих в точечную пробу, закон распределения видоизменяет свою форму (рис. 2.10).
Со значительным увеличением nт закон распределения приближается к
нормальному с моментами:
М(m/nт)=p, s2=pq/nт=p(1- p)/ nт,
где М (m/nт) – математическое ожидание доли кусков определяемого минерала, s2– дисперсия этой доли.
Для случая полного раскрытия биноминальный закон описывает распределение массовой доли определяемого компонента в различных продуктах, при изменении среднего содержания он видоизменяется (рис. 2.11). Если р = 0,5
10
