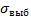Файловый архив студентов. Файловый архив студентов.
1263 вуза, 4625 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский университет «Высшая школа экономики»
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Пособие по математической статистике

.pdf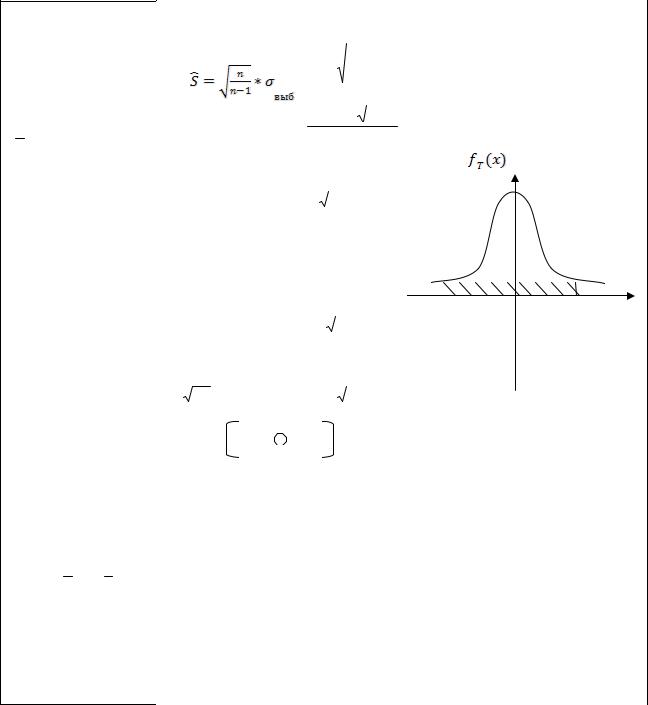
Скачиваний:
207
Добавлен:
02.06.2015
Размер:
4.37 Mб
Скачать
☆

42,539 рублей, выб = 11, 690 рублей. Постройте доверительный интервал для средних ставок по вакансиям в данной отрасли промышленности.

Дано:

- ставки по вакансиям

(m, )

= 42,539

n = 61

S = 11,69 =

= 0,1

= 0,9

( ген неизвестна)

Найти:

Доверительный интервал для математического ожидания

P {m ( ,

)} = 0,9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

 

61

11,69 11,787

 

1.

 

 

 

 

 

 

 

 

 

60

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(

 

 

 

m)

n 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.

Статистика:

Т(k) =

 

 

 

 

 

 

S

 

 

(Распределение Стьюдента)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(42,539 m)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

60

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.

T(60) =

11,787

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(k )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T (k)

 

< t1

 

(60)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.

P{

 

 

2 } = 0,9

 

t 0,95 = 1,671

0,9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(42,539 m)

 

 

 

 

 

 

 

-1,671

1,671

 

 

 

 

 

 

 

 

60

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.

-1,671 <

 

11,787

 

 

 

 

< 1,671

 

 

 

 

 

 

 

 

 

 

 

 

 

19

,696 42,532 m

19,696

 

 

 

 

 

 

 

 

 

 

 

 

60

 

 

 

 

 

 

 

 

 

 

 

60

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

39,9893

 

45,0747

 

 

 

 

 

 

 

6.

7. 2,5427

Ответ: P {m ( 39,9893,45,0747 )} = 0,9

Стр. 111

Задача №10

Консультационной фирме необходимо оценить средний стаж работы менеджеров в фирме «Балтика». Случайная выборка 28 менеджеров показала, что

= 4,2 лет. Предполагается, что ген =2,2 года. Постройте 99% доверительный интервал для среднего стажа работы менеджеров в фирме «Балтика».

Дано:

- стаж работы

(m, )

ген =2,2

= 4,2

n = 28

= 0,01

= 0,99

Найти:

1.Построить

доверительный интервал для М.О:

P {m ( ,

)} = 0,99

2.Какую необходимо

сделать выборку, чтобы 0,99 ?

Решение:

Um

ген

1.

Статистика

 

 

 

 

 

 

 

n

; U N (0,1)

 

 

 

 

 

 

 

 

 

U

4,2 m

 

U1

U 0,995

 

 

 

 

 

 

 

 

2.

 

 

 

 

 

 

 

 

 

 

 

 

2

 

= 2,576

 

 

 

 

 

 

 

 

2,2

 

 

 

 

 

 

 

 

 

 

 

0,99

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

28

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.

 

 

U1

 

 

 

 

 

 

 

 

-2,576

 

 

 

 

 

2,576

 

P{|U| <

2 }=

 

 

 

 

 

 

 

 

 

 

 

 

 

4.

2,576

4,2 m

 

2,576

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2,2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

28

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.

-1,071 < 4,2 – m <1,071

1,071

 

3,129

 

 

 

5,271

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 U 2

 

 

 

 

 

 

 

U

 

n

 

1

2

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

6.

 

 

1

2

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2,2

2 2,5762

 

2,2 2,576

7.

n

 

 

 

 

 

 

 

 

 

 

 

 

128,46

 

 

 

0,52

 

 

0,5

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: P {m (3,129 ; 5,271)} = 0,99; n 129

Стр. 112

Задача №11

Опрос 300 случайно отобранных жителей города «Н» показал, что 55% из них довольны деятельностью вновь избранного мера. Постройте 95% доверительный интервал доли жителей этого города, которые так же доверяют мэру.

Дано:

- число жителей,

которые доверяют мэру (Распределение Бернулли)

A – житель доверяет

P(A) = P*

n = 300

mn

= 0,05

= 0,95

Найти:

Построить

доверительный интервал для P*:

P { P* ( ,

)} = 0,95

Решение:

U

 

P*

 

 

N (0,1) )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,95

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

1

 

U

0,975

1,96

-1,96

 

 

 

 

1,96x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.

 

P{|U| < 1,96} = 0,95

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,55 P*

 

 

 

 

 

 

 

 

1,96

 

 

 

 

 

 

 

 

1,96

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,55 0,45

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

300

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,4973

 

 

 

0,6063

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,0563 0,55 P* 0,0563

3.0,0563

Ответ: P { P* (0,4973 ; 0,6063)} = 0,95

Стр. 113

Задача №12

 

 

Менеджер банка проверяет ежемесячные платежи по

 

счетам. Он сделал

выборку из 100 счетов и вычислил исправленное С.К.О.

3,2 у.е. Какой 95%

S

доверительный интервал для дисперсии построил менеджер?

 

 

Дано:

- платежи по счетам

(m, )

n = 100

S = 3,2

(математическое ожидание генеральное - неизвестно)

= 0,05

= 0,95

Найти:

Построить

доверительный интервал для 2 :

P { 2 ( 1 ; 2 )} = 0,95

Решение:

 

 

 

 

 

 

 

 

 

 

1.

Статистика:

2 n 1

S 2

(n 1)

(распределение 2 , где k = n – 1

 

2

 

 

 

 

 

 

 

 

 

 

– число степеней свободы)

 

 

2.

 

2

(99)

 

2 (99)

74,2

 

 

2

 

0,025

 

 

 

 

 

 

 

 

 

 

 

3.21 2 (99) 2 0,975(99) 129,6

4.P { 2 (99) (74,2 ; 129,6)} = 0,95

 

74,2

3,22 99

129,6

 

 

5.

2

7,82 2

13,7

Ответ: P { 2 (7,82 ; 13,7)} = 0,95

Стр. 114

§3. Задачи для самостоятельного решения

Задача 1

Согласно статистическим данным, средняя семья расходует на развлечения 19,5 у.е. в неделю, ген 5,25 . Для объема выборки n=100 построить доверительный

интервал для математического ожидания m с доверительной вероятностью =0,9.

Задача 2

Менеджер молодежного бара желает оценить средний расход на баночное пиво. Из предыдущего опыта он оценивает с.к.о. расходов на пиво для покупателя в 4 рубля. Если менеджер хотел бы быть уверенным в результате на 90% с предельной ошибкой +/- 5 %, то сколько посетителей бара необходимо отобрать в случайном

порядке

для

получения

такой

оценки.

Примечание:

 

 

4, 0,9 0,1; 0,05; P{m (x ; x )} (

 

 

U

 

. Найти n.

ген

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

Задача 3

 

 

 

 

 

 

 

 

 

 

 

 

Бухгалтер изучает среднюю сумму счетов сервисной компании. Случайная

выборка

 

41

счета

 

 

 

 

 

 

дала

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

выб ; t0,99540 2,7 .

x 16,5 у.е., выб

5,2( ген

не известно), 0,9; 0,01; S

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

Найти доверительный интервал для математического ожидания m с доверительной вероятностью =0,9.

Задача 4

Время обслуживания клиентов, стоящих в очереди, не должно иметь большой вариации, в противном случае – очередь имеет тенденцию к росту. Банк регулярно проверяет время обслуживания образовавшейся очереди к кассиру для определения вариации. Случайная выборка 22 очередников дала значение исправленной

дисперсии S 2 8 (мин). Постройте доверительный интервал для дисперсии времени ожидания в очереди к кассиру банка: P{ ( 1* ; 2*} 0,95.

Примечание: n 22; S 2 8; 0,95; 0,05; 02,(97521) 35,5; 02,(02521) 10,3;

Задача 5

Случайная выборка 225 людей, обратившихся в брачное агентство, показала, что 100 из них нашли себе пару с его помощью. Построить 95% доверительный интервал доли людей, нашедших себе вторую половину через брачное агентство.

Примечание:

n 225; m 100;

m

; 0,95; 0,05; U1

U 0,975 1,96. Найти

 

n

 

 

 

2

 

доверительный интервал для p* : P{p* ( ; )} 0,95

Стр. 115

Задача 6

Число ошибок в ведомости распределено по закону Пуассона с параметром .

Объем выборки: n=100, x 5 .

Найти доверительный интервал для :

P{ (x ; x )} ; 0,9; U

 

U

0,95 1,645.

1

2

 

 

 

 

 

Задача 7

Менеджер по рекламе сети предприятий быстрого питания хотел бы выяснить, знакомы ли студенты петербургских ВУЗов с коммерческой рекламой его предприятий, которая регулярно попадает в СМИ. В случайной выборке 400 студентов 160 ответили, что знакомы с рекламой быстрого питания. Постройте 95% доверительный интервал для оценки доли студентов, знакомых с рекламой предприятий быстрого питания.

 

 

m

 

 

Примечание:

n 400; m 160;

 

0,4;

0,95; 0,05; U1

U 0,975 1,96 .

n

 

 

 

 

2

 

Найти доверительный интервал для p* : P{p* ( ; )} 0,95

 

 

Задача 8

 

 

Предположим, что стоимость выборки 100 рублей за наблюдение. Если известно, что генеральная совокупность имеет D 2 0 , то каким должен быть

объем выборки для оценки среднего значения генеральной совокупности? Какова минимальная стоимость выборки, позволяющая оценить среднее значение генеральной совокупности?

Задача 9

Число ошибок в письменных работах по предмету «социология» распределено по закону Пуассона с параметром . Объем выборки n=60, x 5 , т.е. было выбрано и

исследовано 60 работ, среднее количество ошибок равно пяти. Найти доверительный интервал для : P{ (x ; x )} ; 0,9; U1 2 U0,95 1,645.

(Ответ: P{ (4,525;5,475)} 0,9 )

Задача 10

Случайная выборка 80 посетителей автосалона показала, что 60 из них довольны сервисом и в будущем обратятся в этот салон снова (распределение Бернулли). Построить 95% доверительный интервал доли посетителей, оставшихся

довольными: : P{p* ( ; )} 0,95

(Ответ: P{p* (0,656;0,844)} 0,95 )

Задача 11

Имеем выборку по 10 играм в «монетку». Из них – 3 выигрыша (выпадение «орла»). Построить 95% доверительный интервал доли выигрышей: p* : P{p* ( ; )} 0,95 .

Стр. 116

(Ответ: P{p* (0,259;0,341)} 0,95 )

Задача 12

Число бракованных деталей в одной коробке распределено по закону Пуассона с параметром . Объем выборки n=50, x 1,5 . Найти доверительный интервал для :

P{ (x ; x )} ; 0,9; U1 2 U0,95 1,645. (Ответ: P{ (1,215;1,785)} 0,9 )

Задача 13

Абитуриент сдает экзамен в 10 ВУЗов и проходит по конкурсу в 3 из них (распределение Бернулли). Построить 90% доверительный интервал доли

поступления в ВУЗы : P{p* ( ; )} 0,9 . (Ответ: P{p* (0,053;0,547)} 0,9 )

Задача 14

Секретарь проверяет 200 пакетов документов от поставщиков. Известно, что число ошибок в пакете распределено по закону Пуассона с параметром . Объем

выборки

n=200,

x 1,3.

Найти

доверительный интервал для :

P{ (x ; x )} ; 0,9; U

U0,95

1,645.

1 2

(Ответ: P{ (1,17;1,43)} 0,9 )

Задача 15

Игрок проводит опыт: бросает карту в шляпу 20 раз. Из этих 20 раз карта в шляпу попадает 15 раз (распределение Бернулли). Построить 95% доверительный

интервал доли попадания карты в шляпу : P{p* ( ; )} 0,95 .

(Ответ: P{p* (0,56;0,75)} 0,95 )

Задача 16

В непрозрачном пакете находятся шары с четными и нечетными номерами: 15 человек вытаскивают подряд по одному шару, трое достали из пакета шары с четными номерами. Постройте 90% доверительный интервал для вероятности

вытащить шар с четным номером p* : P{p* ( ; )} 0,9 .

(Ответ: P{p* (0,0355;0,3645)} 0,9 )

Задача 17

В год факультет менеджмента некоторого ВУЗа с дипломом заканчивают 30 человек (n=30). Х – число «красных» дипломов (распределено по закону Пуассона),

x 5,63.

Найти

доверительный

интервал

для

:

P{ (x ; x )} ; 0,95; U

 

U0,975 1,96.

 

 

 

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

(Ответ: P{ (4,92;6,34)} 0,95 )

Стр. 117

ген

Задача 18

Втечение года цены на автомобиль некоторой марки подчинялись

нормальному закону. В среднем, цена на автомобиль была 22,5 тысячи евро,5,27 . Для объема выборки n=100 постройте доверительный интервал для

математического ожидания m с доверительной вероятностью =0,99.

Задача 19

На конвейере предприятия работники собирают подарочные коробки, время в течение которого они собирают 1 коробку не должно сильно отличаться, т.е. иметь большую дисперсию, иначе – конвейер сломается и будут сорваны сроки работы. Главный техник ежедневно засекает время сборки 1 коробки для определения вариации. Случайная выборка 40 работников дала значение исправленной

дисперсии S 2 4 . Постройте доверительный интервал для дисперсии времени сборки одной подарочной коробки: P{ ( 1* ; 2*} 0,95.

Задача 20

Специалист по рекламе изучает средний счет обеда на двоих в новом ресторане

(Х).

Случайная

выборка

60

счетов

дала

 

 

такие

результаты:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

; t 60

 

x 500

руб.,

 

50(

 

не известно), 0,99; 0,01; S

 

 

 

2,66 .

 

 

 

 

 

 

выб

 

ген

 

 

 

 

 

 

n 1

выб

0,995

 

Найти доверительный интервал для математического ожидания m с доверительной вероятностью =0,99.

Стр. 118

Глава 4. Проверка статистических гипотез. Критерий значимости

§1.Основные понятия.

При проведении статистических исследований возникают различные вопросы о свойствах генерального распределения и выборки. Для ответа на эти вопросы выдвигаются гипотезы, требующие статистической проверки на основе полученной выборки.

Эти гипотезы могут быть выдвинуты непосредственно практикой, а могут возникнуть как дальнейший этап статистических исследований после анализа, обеспеченного описательной статистики.

Определение.1. Статистической гипотезой называется предположение о виде или свойствах генерального или выборочного распределений, которые можно проверить статистическими методами на основе имеющейся выборки.

Определение 2. Статистическая гипотеза о генеральном распределении называется простой, если она его полностью определяет. В противном случае гипотеза называется сложной.

Схема применения критерия значимости. Ошибки I и II рода

Постановка задачи

1. Пусть известен закон распределения генеральной совокупности Х, но не

известны параметры ( ) этого закона. Пусть также получена точечная

~

(или интервальная) оценка параметра . Выдвигаются: o Но: 0 (нулевая гипотеза)

o Н 1 : 0 (левосторонняя альтернативная гипотеза) o Н 2 : 0 (правосторонняя альтернативная гипотеза) o Н 3 : 0 (альтернативная двусторонняя гипотеза)

Критерием значимости для параметров гипотез (k) – называется правило,

по которому, на основании выборки, можно сделать вывод: принимать гипотезу или не принимать.

Статистикой критерия k называют СВ z (X1 , X 2 ,...X n ) , по значениям

которой можно применить это правило.

Замечание:

o Будем считать события, вероятности которых очень малы,

невозможными событиями;

o Будем считать события, вероятность которых велика, достоверными.

2.Задается малое число , где - уровень значимости ( =0,1; 0,01; 0,05; 0,001)

3.Пусть V – это множество значений статистики Z. Тогда обозначим Vкр -

критическую область:

o Вероятность того, что значения статистики попадают в критическую

область (при условии, что выполняется гипотеза Но):

P{Z Vкр / Ho}

o Вероятность того, что значения статистики не попадают в

критическую область, а попадают в область принятия решения

Стр. 119

o «V \ Vкр »: P{Z (V \ Vкр ) / Ho} 1

Общая схема проверки параметрических гипотез

1.Выдвигается нулевая (проверяемая) гипотеза Но, а также альтернативные гипотезы: Н 1 , Н 2 , Н 3 .

2.Выбирается уровень значимости (обычно 0,001; 0,01; 0,05; 0,1).

3.Выбирается статистика Z критерия значимости и соответствующая ей, уровню значимости и проверяемым гипотезам Но, Н1 1 , Н1 2 , Н1 3 критическая область Vкр , являющаяся частью области V значений статистики Z. При это V \ Vкр будет областью допустимых значений Z.

4.Вычисляется выборочное значение Zвыб статистики Z (по данной

выборке).

5.Критерий (правило) принятия решения:

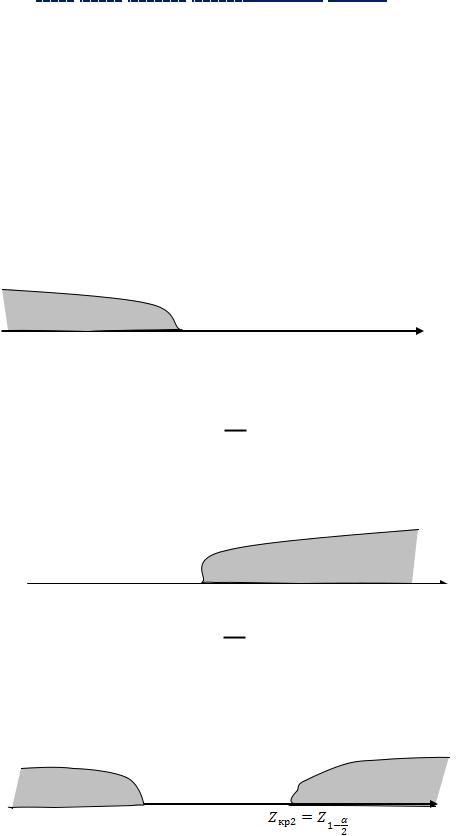
oДля левосторонней гипотезы:

Н1 : 0 ; P{Z Zкр / Но} =

Критическая обл.

Область принятия решения

 

 

 

 

 

 

Zкр

Z - квантиль порядка

 

х

 

 

 

 

 

Правило принятия решения : Если zвыб zкр , то гипотезу Но на

уровне значимости отвергаем в пользу альтернативной. Если zвыб zкр , то гипотезу Но принимаем на уровне значимости .

oДля правосторонней гипотезы:

Н 2 : 0 ; P{Z Zкр / Но} =

Область принятия решения

Критическая обл.

 

Zкр

Z1 - квантиль порядка (1- )

х

Правило принятия решения : Если zвыб zкр , то гипотезу Но на

уровне значимости отвергаем в пользу альтернативной. Если zвыб zкр , то гипотезу Но принимаем на уровне значимости .

oДля двусторонней гипотезы:

Н 3 : 0 ; P{Z (Zкр1 ; Zкр 2 ) / Но}

Критическая обл. 2 Область принятия решения Критическая обл 1

Z

кр1 Z / 2

х

 

Стр. 120

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности