1) Для любой al(al)

;

2).

ДОКАЗАТЕЛЬСТВО. Нетрудно видеть, что

,

где _a – частота буквы «a» в последовательности A_L. Отнесем к первой группе (A^L)^ те и только те последовательности A_L, в которых

для некоторой >0. Ко второй группе отнесем все остальные последовательности.

Покажем, что при достаточно большом L₀ это разбиение удовлетворяет обоим условиям теоремы. Действительно, для

.

Отсюда нетрудно показать, что

.

Следовательно,

.

Полагая

,

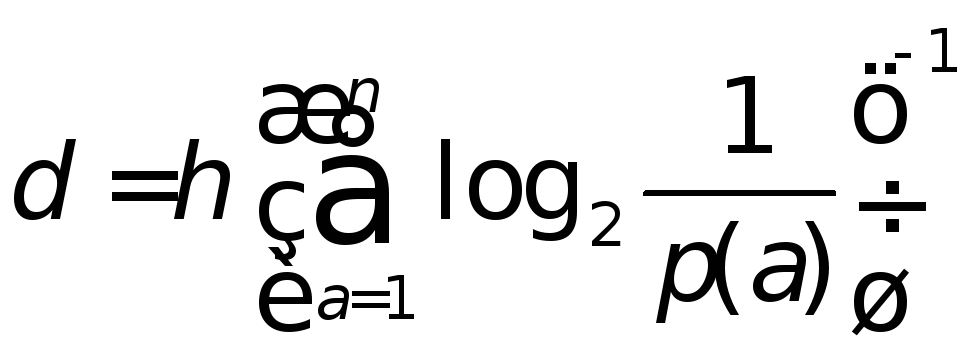получаем первое утверждение теоремы.

Рассмотрим вторую группу (A^L)^. Нетрудно видеть, что вероятность

По неравенству Чебышева

откуда следует, что

Полагая L₀=n/², получаем второе утверждение теоремы.

СЛЕДСТВИЕ. Если LL₀, то для любой A_L(A^L)^ выполняется неравенство

.

Таким образом, при достаточно больших L вероятность каждой последовательности из (A^L)^ (за исключением последовательностей весьма маловероятного класса) заключена между 2^-L(H+) и 2^-L(H-).

Важно бывает знать мощности обоих групп последовательностей (см. первую теорему Шеннона). В частности, возникает вопрос о числе «наиболее вероятных» последовательностей, вероятности которых приблизительно равны .

Занумеруем все последовательности A_L в порядке убывания их вероятностей:

.

Выберем , 0<<1. Пусть N_L() – число последовательностей, определяемых из неравенства

.

В это число войдет некоторое число последовательностей А_L второй группы, у которых Р(А_L)>2L(Н(А)-), но в основном оно определяется последовательностями первой группы.

Вторая теорема Шеннона. Для любого фиксированного значения , 0<<1 справедливо соотношение

.

ИМЕННО В ЭТОМ СМЫСЛЕ ПИШУТ, что N_L()=2^LН(А). Как следует из формулы, этот предел не зависит от  и поэтому можно полагать  сколь угодно близким к 1, =1- и тогда n^L– N_L(1–) есть число последовательностей, вероятность появления которых в результате реализации нашего случайного процесса получения последовательностей пренебрежимо мала, то есть практически невозможных последовательностей.

Доказательства приведенных теорем обычно даются в курсе математической теории информации.

Таким образом, в первой и второй теоремах Шеннона устанавливается замечательное свойство «равнораспределенности» длинных сообщений, порождаемых независимыми испытаниями схемы А.

Это свойство устанавливает, грубо говоря, тот факт, что всего таких сообщений

N_L2^LH(A) и все они приблизительно равновероятны.

Можно ли установить похожее свойство для осмысленных сообщений, которые, очевидно, не порождаются независимыми испытаниями?

Для этого необходимо, во-первых, ввести математическую модель осмысленных сообщений, а во-вторых, определить, в соответствии с (1), энтропию на одну букву осмысленного сообщения. В качестве математической модели осмысленных сообщений обычно рассматривают последовательности, получаемые с помощью так называемых марковских процессов. Среди таких процессов имеется важная группа процессов называемая стационарными эргодическими процессами. В таких процессах каждая создаваемая процессом последовательность имеет одни и те же статистические свойства. Поэтому относительные частоты различных комбинаций исходов (букв, биграмм и т. п.), полученные из частных последовательностей будут стремиться с увеличением длин последовательностей к определенным пределам, не зависящим от этих частных последовательностей. Таким образом, для эргодического процесса возможно отождествление средних значений различных комбинаций исходов вдоль некоторой последовательности со средними значениями по ансамблю возможных последовательностей (причем вероятность расхождения равна нулю).