Глава 8.

Общее понятие информации. Способы представления информации, подлежащей шифрованию. Дискретизация непрерывных сигналов

Теорема Котельникова. Объектом криптографии является информация (содержание сообщений) в процессе ее передачи по каналу связи. Поэтому, как правило, изучение криптографии как науки начинают с изучения свойств открытой информации. Криптографы дают следующее определение открытой информации: «незасекреченная (незашифрованная) информация, предназначенная для передачи по каналу связи». Открытая информация обязательно должна быть зафиксирована на каком-либо материальном носителе (на бумаге, фотопленке, перфоленте и т. д.) Открытую информацию, зафиксированную на некотором материальном носителе, принято называть открытым сообщением.

Открытая информация обладает свойством инвариантности относительно материального носителя и заранее оговоренной формы ее представления (например, в естественной форме – в виде текста на каком-либо языке, либо в искусственной форме, например, в виде двоичной последовательности, последовательности физических сигналов и т.д.).

Общеизвестно, что имеется возможность представления непрерывных сигналов ограниченного спектра в виде последовательности дискретных сигналов без потери информации.

ТЕОРЕМА Котельникова В.А. Непрерывная функция S(t), спектральная плотность которой отлична от нуля только в интервале (–F,F), полностью определяется своими значениями, отсчитанными в дискретных точках через интервал t=, гдеF – максимальная частота спектра (равная ширине спектра в случае, если он начинается от нуля). Значения функции S(t) в любой точке t выражается формулой

S(t)=,

где S(кt) – отсчеты непрерывной функции в дискретных точках t=кt.

Обычно реальные непрерывные сообщения и сигналы приблизительно можно рассматривать как функции с ограниченным спектром. Поэтому в силу теоремы Котельникова вместо непрерывных сообщений можно рассматривать соответствующие им дискретные сигналы (без потери информации).

Классификация сигналов. Физически сигнал реализуется в виде некоторого модулированного колебания. Если значения сигнала можно точно предсказать в любой момент времени, то он называется детерминированным. Примером непрерывных детерминированных сигналов являются импульсы или пачки импульсов, форма, амплитуда и положение во времени которых точно известны.

Все детерминированные процессы можно разделить на два класса: периодические и непериодические. Процесс S(t) считается периодическим, если его значения точно повторяются через одинаковые отрезки времени T, величина которых называется периодом:

Если такого отрезка времени нельзя указать, то процесс является непериодическим. Периодические процессы делятся на гармонические и полигармонические. Класс непериодических процессов состоит из почти периодических процессов и переходных процессов. Реально могут существовать любые комбинации этих процессов. Рассмотрим методы представления сигналов этих классов.

В качестве носителя сигналов часто рассматривается гармоническое колебание, изменяющееся в соответствии с выражением , где:S_m – амплитуда;  – круговая частота;  = 2f; f – частота в герцах;  – начальная фаза. Это колебание является периодической функцией с периодом T= f ^–1. Частным случаем гармонического сигнала (при частоте  = 0) является постоянный уровень. Гармонические колебания – это наиболее простой вид непрерывных периодических процессов. Сам по себе бесконечный во времени гармонический процесс не является сигналом и не несет информации. Носителем информации он становится после модуляции одного или нескольких его параметров другим процессом, связанным с сообщением.

Полигармонические сигналы образуются любыми периодическими процессами, отличными от гармонических. Если некоторый процесс S(t) с периодом T удовлетворяет условиям Даламбера, т. е. является непрерывным везде, кроме, может быть, счетного множества точек разрыва 1 рода, и имеет конечное число экстремумов, то он может быть представлен на интервале периода [0,T] совокупностью базисных функций в виде суммы

, (1)

где: _k(t) – k–я базисная функция; С_k – весовые коэффициенты. При этом предполагается, что

,

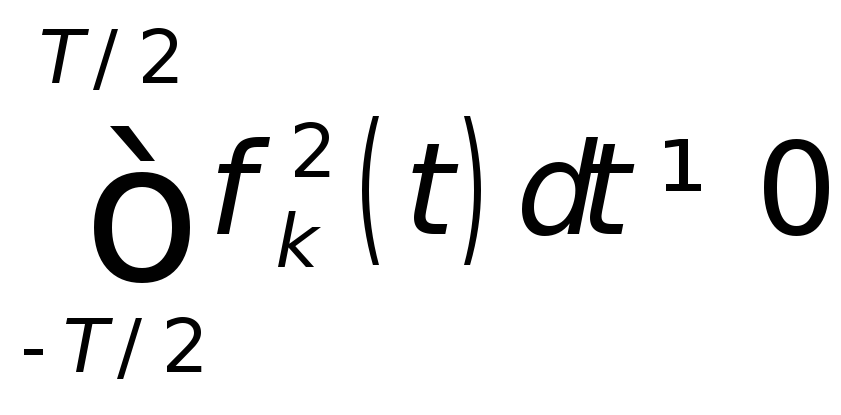т.е. никакая из функций базисной системы не равна тождественно нулю на интервале периода [0,T]. Система функций {_k(t)} называется ортогональной, если для любой пары k и l, исключая k=l, выполняется равенство

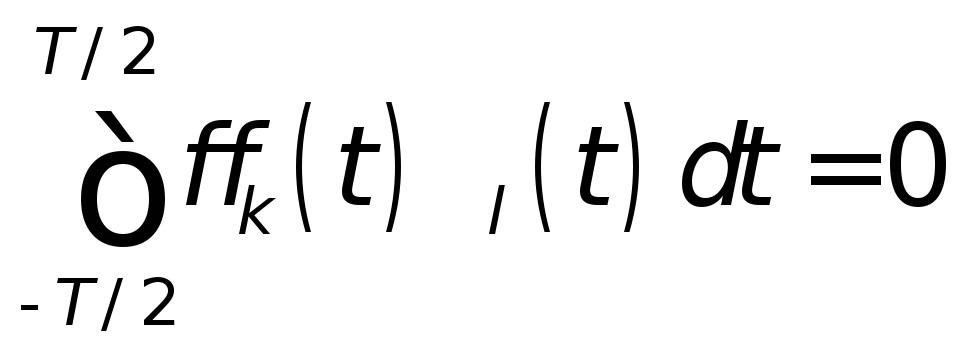. (2)

Если, при l= k

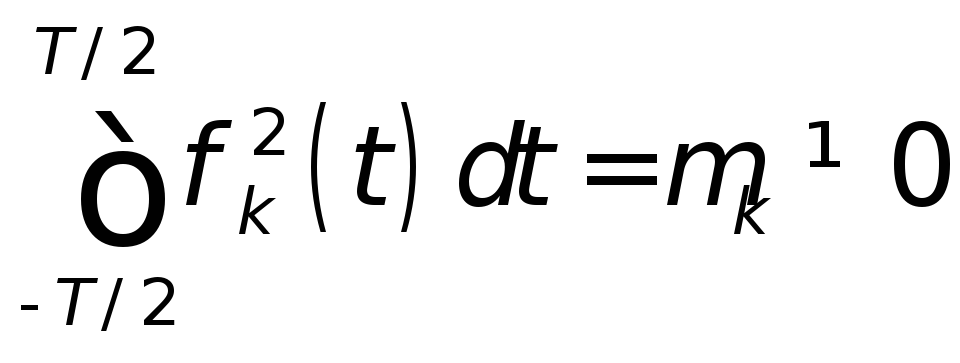, (3)

то величина называется нормой функции_k(t) и обозначается . Если норма функций ортогональной системы равна 1, то такая система функций называется ортонормированной. Для определения коэффициентовС_k в разложении функции S(t) в ортогональном базисе рассмотрим выражение

.

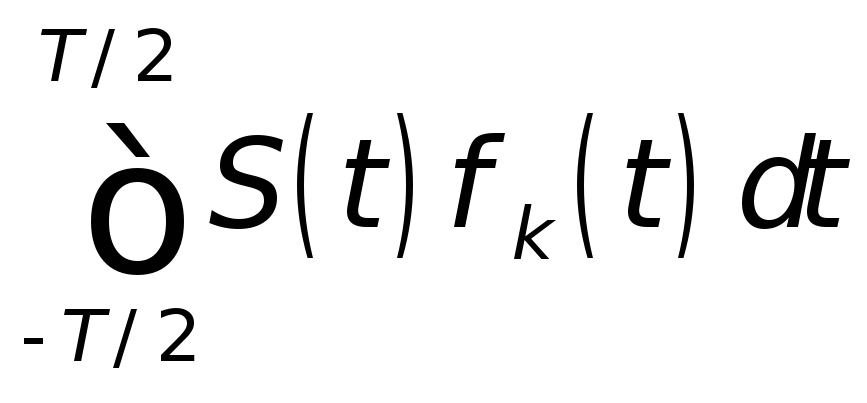Представив в подынтегральном выражении S(t) в виде его разложения (1) и учитывая (2) и (3), получим:

.

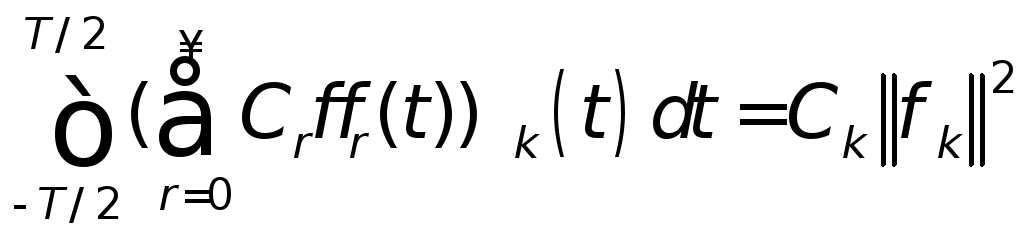Из последнего выражения находим значение коэффициента С_k:

. (4)

Сумма (1) с коэффициентами, определяемыми по (4) называется обобщенным рядом Фурье по данной системе базисных функций {_k(t)}. Обобщенный ряд Фурье обладает важным свойством: при заданной системе базисных функций и фиксированном числе N его слагаемых он обеспечивает наилучшую аппроксимацию (в смысле среднеквадратической ошибки) заданной функции S(t). При заданной системе базисных функций {_k(t)} сигнал S(t) полностью определяется набором весовых коэффициентов C_k. Этот набор называется дискретным спектром сигнала.

Для любой ортогональной системы справедливо неравенство Бесселя

.

Ортогональная система называется полной, если увеличением числа N членов ряда среднеквадратическую ошибку аппроксимации можно сделать как угодно малой. Условие полноты может быть представлено в виде выражения

.

Величину называют энергией сигнала. Для энергии сигнала получаем

(5)

или для ортонормированной системы базисных функций

.

Пояснения к выводу теоремы Котельникова. Как отмечалось выше в теории анализа сигналов и технике связи широкое применение находит теорема Котельникова (теорема отсчетов), в соответствии с которой функция S(t) полностью определяется последовательностью своих значений в моменты времени, взятые с интервалами не более продолжительными, чем 1/2f_в, если наибольшая частота в спектре этой функции меньше f_в. В этом случае функция S(t) может быть представлена выражением

, (6)

где– интервал времени между двумя соседними отсчетами сигнала S(t), а S(kt) – отсчеты функции S(t) в моменты времени ,

.

Функции вида встречаются при исследовании спектра одиночного прямоугольного импульса. Эти функции образуют систему ортогональных функций с интервалом ортогональности, равным бесконечности, и нормой

.

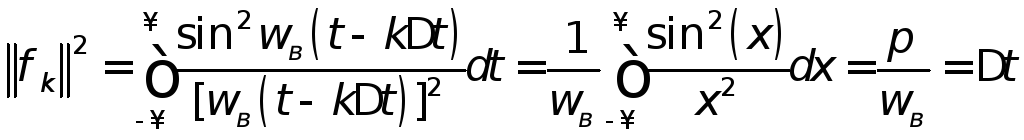Покажем, что разложение сигнала S(t) в этом базисе дает спектр, действительно состоящий из отсчетов сигнала S(kt). Предварительно условимся, что энергия сигнала конечна, т. е. S(t) является квадратично–интегрируемой функцией. Кроме того, отметим, что ,приnk.

Напомним, что понятие спектральной плотности сигнала S(t) определяют с помощью преобразования Фурье S()=, где е^–it=cost–isint. S() называют спектральной плотностью сигнала S(t) (в общем случае это копплексное число). Спектральная плотность одиночного импульса S₁(t) на частоте =к₁ равна S₁()== =, где [t₁,t₂] – интервал существования импульса. Выражение S(t)=называютобратным преобразованием Фурье.

Спектральная плотность функции равна

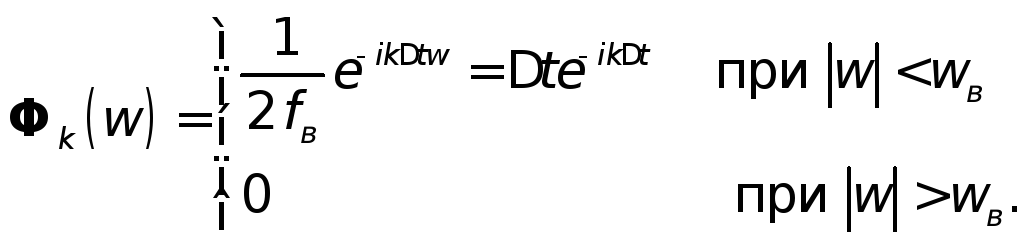
Отсюда следует, что модуль спектральной плотности любой базисной функции в полосе частотимеет постоянное значение, равное.

Определим значения коэффициентов разложения, применяя формулу (4): периода гаммы в шифре гаммирования по заданному шифртекступериода гаммы в шифре гаммирования по заданному шифртексту

. (7)

Для вычисления интеграла в этом выражении воспользуемся известным соотношением, устанавливающим связь между произведением двух функций f(t) и g(t)и произведением их спектров плотностей F() и G()

,

где – функция комплексно–сопряженная кG(). В соответствии с этим свойством

,

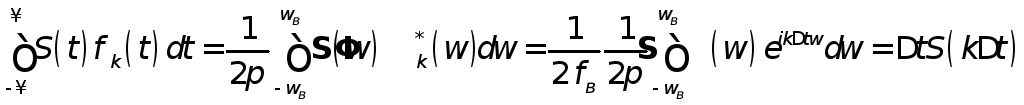где пределы интегрирования берутся равными граничной частоте _в спектра сигнала и базисных функций. Подставляя полученное значение интеграла в (7), имеем окончательное выражение для коэффициента разложения

,

т. е. коэффициентами ряда Котельникова являются отсчеты сигнала в моменты времени , как это было определено в (6). Ряд (6) сходится к функцииS(t) при любых значениях времени t, т. к. вследствие ограниченности верхней частоты сигнала он является непрерывным.

Если отсчеты сигнала S(t) берутся с интервалами , то ширина спектра базисных функцийсовпадает с шириной спектра сигнала и представление сигнала соответствует (6). Если взять интервал между отсчетами равным, то ширина спектра соответствующих базисных функций будет превышать спектр сигналаS(t), что повышает точность представления этого сигнала. При этом исключается возможность отбрасывания «хвостов» спектра S() вне граничных частот. Если интервал , то спектр соответствующей базисной функции становится уже спектра сигналаS(t) и коэффициенты C_k в выражении (7) становятся отсчетами не этого сигнала S(t), а некоторого другого сигнала, спектр которого ограничен другой частотой .

Решение реальных задач связано с сигналами, одновременно ограниченными и по частоте и по времени. Теоретически эти условия являются несовместимыми. Практически эти ограничения определяют таким образом, чтобы основная часть энергии сигнала была заключена в пределах выбранной длительности этого сигнала и ширины его спектра, а на долю «хвостов» приходилась бы только незначительная ее часть. При таком подходе для сигнала длительностью T и верхней частотой полосы пропускания f_в число независимых отсчетов, необходимое для полного задания сигнала, равно

.

В этом случае ряд (6) может быть представлен следующим образом

.

Число N называют базой сигнала или числом степеней свободы сигнала. Учитывая (5), можно представить энергию и среднюю мощность сигнала через последовательность его отсчетов

,

.

Последнее выражение показывает, что средняя мощность непрерывного сигнала на интервале T равна среднему квадрату отсчетов, умещающихся на этом интервале через промежутки 1/2f_в.

Процедура представления непрерывного сообщения в дискретную форму называется квантованием сигнала во времени (дискретизацией). В связи со сказанным выше особое значение приобретает изучение свойств дискретных сообщений. Далее основное внимание будет уделено именно им. При этом основное внимание будет сосредоточено на изучении свойств так называемых открытых текстов.