6.3. О дешифровании фототелеграфных изображений

Для дешифрования не требуется особых усилий, если открытая информация имеет высокую избыточность. Это характерно для фототелеграфных изображений. Шифрование черно-белых картинок обычно осуществляется следующим образом. Картинка разбивается на квадратики. Квадратик закрашивается в черный цвет – 1, если большая его часть черная, и в белый цвет – в противном случае. Таким образом, каждому изображению ставится в соответствие последовательность из 0 и 1. При шифровании на эту последовательность накладывается гамма, снимаемая с шифратора.

Если посмотреть на изображение, зашифрованный последовательностью, полученный по равновероятной схеме Бернулли (полученный бросанием симметричной монеты), то мы увидим серый фон. Если же гамма неравновероятна, то на изображении проявляются контуры фигур, и чем больше неравновероятность, тем контуры отчетливее. На приводимых ниже рисунках приведено изображение черного квадрата на белом фоне, закрытое с помощью неравновероятной гаммы. Вероятность единицы в гамме указана в процентах (0%, 42%, 50%, 70%).

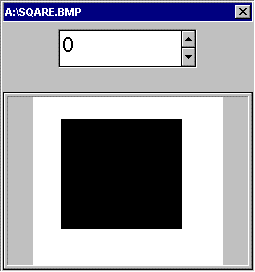
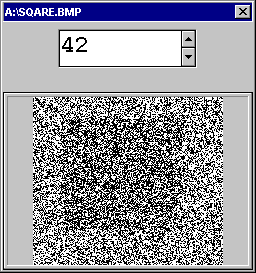
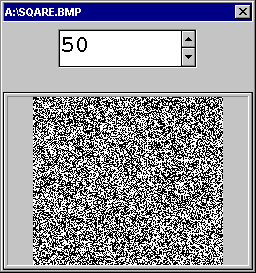
В связи с выше изложенным, обязательная составная часть криптографии – это исследование вероятностно-статистических свойств выходных и промежуточных гамм. Для этих целей можно использовать стандартные статистические критерии проверки качества псевдослучайных последовательностей см. [Кнут. «Искусство программирования». Т. 2.], либо специально разработанные статистические процедуры.

О степени неоднозначности восстановления открытого текста. Достаточно частой является ситуация, когда гаммы или открытый текст можно восстановить приближенно по побочным сигналам, сопровождающим работу криптотехники и оборудования. Представьте, например, что открытый текст печатается на телетайпе. Каждый удар печатающего устройства вызывает шум, все телетайпы стучат, и стук немного отличается для каждой буквы. Вопрос для инженера – выявить эти отличия для разных букв. Задача криптографа – оценка насколько это опасно.

Для оценки используются методы теории информации. Самая грубая оценка степени неоднозначности восстановления открытого текста длины N для приведенного выше примера (шифрования гаммой, принимающей k значений) имеет вид

r=2^NH,

где n – мощность алфавита открытого (шифрованного текста), H – энтропия открытого текста на букву.

Таким образом, дешифрование принципиально возможно для литературного открытого текста (H=1), если шифрующая гамма принимает kвозможных значений, т.е. k16 (положимn=32, Н=1, решая уравнение

,

получим k=16).

Реальное дешифрование обычно удавалось провести при k. Высококлассные специалисты добивались дешифрования где-то при k=12.

Для шифрования не равновероятной гаммой оценки приобретают вид

r=,

где H– энтропия гаммы.

6.4. Дешифрование шифра гаммирования при перекрытиях

Перекрытием шифра называется ситуация, при которой два открытых текста шифруются с использованием одной и той же гаммы, управляющей работой узла наложения шифра. Возникновение перекрытий – это опасная с точки зрения надежности защиты ситуация. Особенно неприятна она для шифраторов гаммирования. В этом случае в распоряжении противника оказываются два шифрованного текста вида

b¹_t=a¹_t+_t и b²_t=a²_t+_t , t{1,2,…,N}.

Обращаем внимание, что открытый текст и шифрованный текст здесь разные, а гамма одинакова. Злоумышленнику нетрудно из шифрованных текстов получить разность двух открытых текстов.

a– a= b-b= c_t

и попытаться восстановить оба открытых текста. Это просто сделать, если один из открытых текстов известен, в этом случае

a=c_t+a

где c_t и a– известны, а a– легко восстанавливается. Открытый текст a– может быть известен, в случае, если аппаратура работала в линейном режиме (постоянная связь между передатчиком и приемником), при этом в течение некоторого времени содержательной информации не передавалось, и шифровался известный всем текст «нет информации».

Если шифруются обычные тексты и ни один из них неизвестен, то для дешифрования используют стандарты.

Опробуют слово открытого текста и пытаются восстановить второй открытый текст. Если вариант опробования был выбран неправильно, то второй открытый текст будет бессмысленным, если правильно – то осмысленным, и так по частям мы восстановим оба открытых текста.

Например, предположим, что в один из текстов начинался со слова «СЕКРЕТНО». В этом случае, подставив его на нужное место мы восстановим фрагмент второго текста, например,

С Е К Р Е Т Н О

В О Е Н Н О – М

Угадав продолжение фрагмента второго текста, мы получаем продолжение первого текста

С Е К Р Е Т Н О С О О Б Щ

В О Е Н Н О – М О Р С К О Й

Продолжая первый текст, получаем

С Е К Р Е Т Н О С О О Б Щ А Ю

В О Е Н Н О – М О Р С К О Й Ф

Снова обращаемся ко второму тексту

С Е К Р Е Т Н О С О О Б Щ А Ю В А М

В О Е Н Н О – М О Р С К О Й Ф Л О Т

Таким образом, дешифровальщик восстанавливает оба текста.

b¹_t=a¹_t+_t и b²_t=a²_t+_t ,

Если есть две криптограммы y и y’ (или два куска криптограмм), то возникает вопрос о том, можно ли узнать до протяжки вероятного слова о том, зашифрованы ли они одной и той же гаммой . Для решения данной задачи рассмотрим простейшую модель открытого текста – последовательность независимых испытаний по полиномиальной схеме с вероятностями p(a),..., p(a) (распределение Р). Тогда случайная величина  = – имеет распределение Р=P*P, где Р – свертка распределения Р с собой. Если Р – неравновероятное распределение, то Р=(p(a),...,p(a)) также неравновероятное распределение. Тогда – независимые случайные величины с распределениемР. Если a зашифровывается с помощью , а a’ – с помощью ‘, то

b – b’ = a -ax’ +  – ‘.

В наших предположениях  – ‘ – равновероятно распределенные случайные величины. Следовательно, b – b’ – также независимые и равновероятно распределенные случайные величины. Значит, статистический критерий, проверяющий гипотезу Н о равновероятности y – y’ против альтернативы Н, что y – y’ имеет распределение Р, дает ответ о наличии перекрытия в y и y’.

Обычно схема получения гаммы следующая: имеется автономный автомат А, в котором начальное состояние есть ключ k. Выходная последовательность этого автомата есть гамма  для шифрования. Например, регистр сдвига с линейной и нелинейной обратной связью. При таком способе получения  повтор  получается, когда автомат начинает вырабатывать периодическую последовательность. Если период небольшой, то его можно опробовать и, применяя критерий на перекрытие, найти, а затем дешифровать криптограммы. Если n –число состояний автомата велико, то можно получить большой период, а, следовательно, мало шансов на перекрытие.

Пусть S={1,…,n} – множество состояний автомата А, h – функция переходов, s₁=k – случайное начальное состояние. Рассмотрим вопрос о периоде состояний автономного автомата А Период возникает, когда возникает повторение в последовательности состояний s₁,h(s₁), h(s₁),.... Пусть h – случайная равновероятная подстановка на {1,…,n}. Тогда возврат возможен только в точку k. Если  – длина полученного цикла, и случайная величина  = 1, если длина цикла равна i, и  = 0 в противном случае, то

P( = 1) = .

Тогда

t = .

Отсюда

Et = ==.

При n = 2E  10, что дает мало шансов ожидать перекрытия даже при очень большой интенсивности переписки.

Если А – случайное отображение (не взаимно-однозначное) и  – длина цикла, а h – длина подхода, то тогда h ~ , ~ иh+ ~ . Следовательно, приn = 2h+ ~ 2~ 10, что является не очень большой величиной и можно ожидать перекрытия гаммы.

Обращаем внимание на то, что наличие перекрытий шифра опасно для абсолютно стойкого шифра гаммирования. Перекрытия шифра – это одна из самых больших неприятностей, которая практически может иметь место для этих шифров. Для избежания перекрытий абсолютно стойких шифров гаммирования обычно применяют как организационные методы, сводящиеся к уничтожению гаммы наложения сразу же после первого использования так и технические методы, состоящие, например, в построении псевдослучайных последовательностей гарантированного периода. Отметим также, что для обеспечения криптографической стойкости поточных шифров простой замены их управляющие блоки (УБ) и шифрующие блоки (ШБ) должны удовлетворять целому ряду требований, одно из которых состоит в обеспечении больших периодов выходных последовательностей УБ и больших периодов последовательностей шифрпреобразований ШБ. В терминах теории автоматов эти вопросы будут решаться в томе 2.