Где  принадлежит множеству к подстановок на I (p-1(j) – вероятность j-той буквы, для ее расчета исходя из набора (p1,p2,…,p|I|) необходимо найти --1(j) – образ буквы j при подстановке --1).

Предположим, что множество К подстановок таково, что при любых различных ,`,*К величины MI<sub>c</sub>(P(<sup>-1</sup>),P(`^-1))=и MI_c(P(^-1),P(*^-1))=остаточно сильно различаются, то есть различаются так, что различаются и взаимные индексы совпадения MI_C((), (`)), MI<sub>C</sub>((),(*)) для выборок (), (`),(*) из распределений P(^-1), P(`^-1), P(*^-1).

Приведенное выше приближенное равенство (,) является основным средством решения следующей задачи. При известных значениях МI_c(P(^-1), P(`<sup>-1</sup>)), MI<sub>c</sub>(P(<sup>-1</sup>),P(*<sup>-1</sup>)) и известной подстановке  найти ` и * по реализациям выборок: (), (`), (*) из распределений

P(^--1), P(`^-1), P(*^-1).

Для решения этой задачи подсчитывают взаимные индексы совпадения MI_C((),(`)), MI<sub>C</sub>((),(*)) выборок (), (`) и (), (*) и определяют по ним приближенные значения величин MI_c(P(^-1),P(`<sup>-1</sup>)) и MI<sub>c</sub>(P(<sup>-1</sup>),P(*<sup>-1</sup>)). Откуда узнают и неизвестные ` и *.

Метод Симпсона. Перейдем теперь к изложению метода дешифрования шифра последовательной замены при известном периоде ключевой последовательности.

Пусть b₁,b₂,…,b_N – известный шифртекст, d – период ключевой последовательности.

Для всех возможных пар (,`) из КхК подсчитывается значение вероятности МIc(P(<sup>-1</sup>), P(`^-1)). Проводится разбиение множества К на классы kК эквивалентности так, что пары из одного класса имеют одинаковое значение вероятности, а из разных классов k, k` – разное значение вероятности.

Выписывают шифртекст в следующем виде:

(1) b₁, b_1+d, b_1+2d,…,b_1+jd,…

(2) b₂, b_2+d, b_2+2d,…,b_2+jd,…

……………………………..

(d) b_d, b_d+d, b_d+2d,…,b_d+jd…

Пусть ₁,₂,…,_d – начальный отрезок неизвестной ключевой последовательности. Тогда первая строка букв – последовательность (1) результат шифрования букв открытого текста по простой замене ₁, вторая – (2) – по _2, …d-тая – по _d. Далее предполагают, что каждая последовательность (j) является реализацией выборки из неизвестного вероятностного распределения . Подсчитываются значения взаимных индексов совпаденияMI_C((1),(j)), j{1,…,d}. Опробуют в качестве неизвестной подстановки ₁ все подстановки  из К. Для опробуемого варианта  при каждом фиксированном j{1,…,d} проводят сравнение значения взаимного индекса совпадения MI_C((1),(j)) с вероятностями: MIс(P(^-1),P(`<sup>-1</sup>)), `К. Для каждого j{1,…,d} находят наиболее близкое значение MIс(P(^-1),P(`^-1)). Этому значению отвечает некоторый класс эквивалентности к(j). Опробуемому варианту  ставят в соответствие множество {,k(2),…,k(d)} значений вариантов начального отрезка ₁,₂,…,_d ключевой последовательности. Первый элемент любого такого варианта есть , второй – произвольный элемент из класса k(2), и т. д. Промежуточным этапом решения задачи является получение объединения множеств вариантов по всем К. Далее, поставленная задача дешифрования решается опробованием вариантов этого множества.

Отметим, что опробование неизвестной подстановки ₁ диктуется неоднозначностью решения уравнения = P относительно пары подстановок (,*). Так, если (,*) – решение этого уравнения, то пара (^,*^) также будет решением рассматриваемого уравнения при любой подстановке ^. Если же ищутся решения (,*) с заданной первой компонентой , то неоднозначность решения значительно уменьшается.

Модернизированный метод Симпсона. Если известно, что первая подстановка ₁ начального отрезка ₁,₂,…,_d ключевой последовательности равна тождественной подстановке, то (1)=b₁, b_1+d, b_1+2d,…,b_1+jd является выборкой из неизвестного открытого текста и, по предположению, она трактуется как выборка из распределения Po. В этом случае по значениям вероятностей MIc(Po,P(-1)), К с помощью вычисленных значений взаимных индексов совпадения MIC((1), (j)), j{1,…,d } определяются остальные значения ключевой последовательности.

При неизвестной же первой подстановке в качестве выборки из неизвестного открытого текста (выборки из распределения P_o=(P₁,P₂,…,P_|I|)) может быть взят произвольный содержательный текст (0), т.е. можно ввести дополнительную вспомогательную последовательность (0) и считать, что ее буквы шифровались по тождественной подстановке. Следовательно, в общем случае имеется возможность сведения данной задачи к задаче дешифрования при известной первой подстановке. Практически же предлагается провести вычисления модернизированного взаимного индекса МВЗ(P_o,(j)) по формуле

ВЗ(P_o,(j))= ,

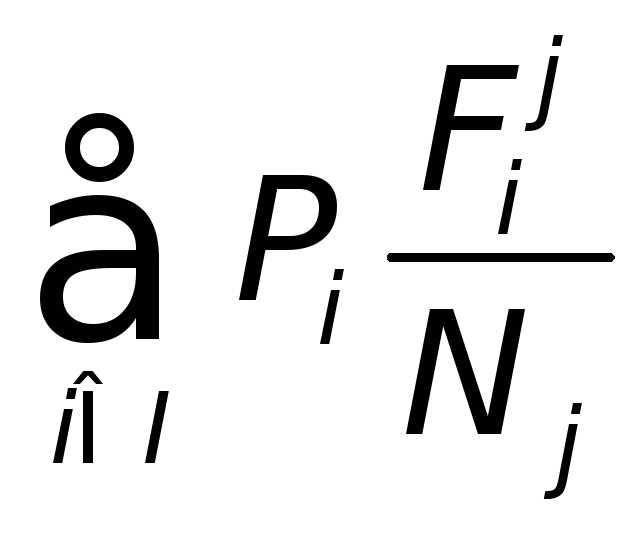где N_j – длина последовательности (j), F– частота буквы i в(j). В качестве искомой подстановки _j предлагается брать подстановки , для которых

ВЗ(P_o,(j))= 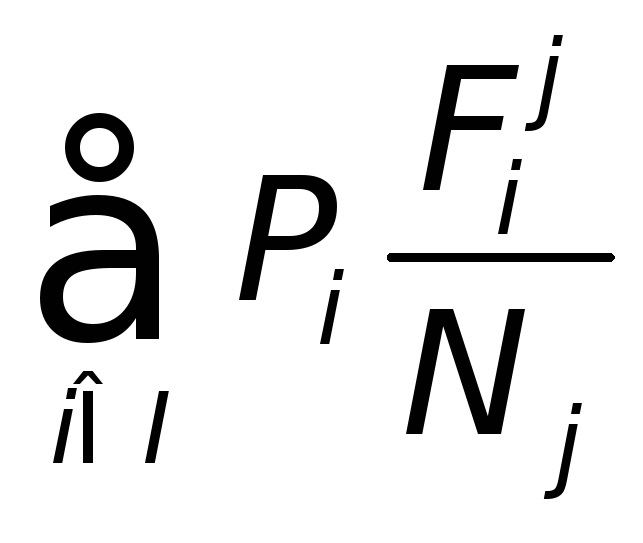MI_c(P_o,P(^-1))= .