1.2. Примеры моделей шифров

Обозначим через I некоторый алфавит, а через I* -множество всех слов в алфавите I, то есть множество конечных последовательностей (i₁,i₂,…,i_L), i_jI, j{1,…,L}, L{1,2,….}

Шифр простой замены. Пусть Х=М – некоторое подмножество из I*, а К – множество всех подстановок на I, т.е. К=S(I) – симметрическая группа подстановок на I. Для каждого gК определим f_g , положив для (i₁,i₂,…,i_L) из М f_g(i₁,i₂,…,i_L)=g(i₁),g(i₂),…,g(i_L). Положим дополнительно

f(i₁,i₂,…,i_L, g)=f_g( i₁,i₂,…,i_L)

и У=f(М)={f(i₁,i₂,…,i_L,g): gS(I), (i₁,i₂,…,i_L)М}. Таким образом, нами определен шифр А=(М, S(I), У, f) простой замены, более точно: алгебраическая модель шифра простой замены с множеством открытых текстов Х=М.

Шифр перестановки. Положим Х – множество открытых (содержательных) текстов в алфавите I длины кратной Т. К=S_Т – симметрическая группа подстановок степени Т, для gS_Т определим f_g положив для (i₁,i₂,…,i_Т)Х

f_g(i₁,i₂,…,i_Т)=(i_g(1),i_g(2),…,i_g(Т));

доопределим f_g на остальных элементах из Х по правилу: текст хХ делится на отрезки длины Т и каждый отрезок длины Т шифруется на ключе g по указанному выше закону шифрования. Последовательность, составленная из букв образов зашифрованных слов, является шифрованным текстом, соответствующим открытому тексту х и ключу g. Таким образом, нами определена функция f:ХКУ и шифр перестановки (Х,S_Т,У,f). Для шифрования текста длины не кратной Т его дополняют буквами до длины кратной Т.

Шифр гаммирования. Пусть буквы алфавита I упорядочены в некотором естественном порядке. «Отождествим» номера этих букв с самими буквами. То есть формально положим I={1,2,…,n}, |I|=n. Положим Х – некоторое подмножество множества I^L, КI^L. Для ключа =₁,₂,…,_L из К и открытого текста х= i₁,i₂,…,i_L их Х положим f_(i₁,i₂,…,i_L)=y₁,y₂,…,y_L, где y_j=i_j+_j mod(n), j{1,…,L}. Иногда под шифром гаммирования понимают и следующие способы шифрования: y_j=i_j-_j; y_j=_j – i_j mod(n).

Шифр дискового шифратора. Пусть I={1,2,…,n}, открытый текст i₁,i₂,…,i_L будет шифроваться с помощью последовательности подстановок ₁,…, _j,…, _L из симметрической группы подстановок степени n. Именно, f_k(i₁,i₂,…,i_L)= ₁(i₁),…, _j(i_j),…,_L(i_L). Выбор ключа k будет пояснен позднее.

При такой его интерпретации сначала объясним правило зашифрования дискового шифратора с одним диском (рис.1.2.1).

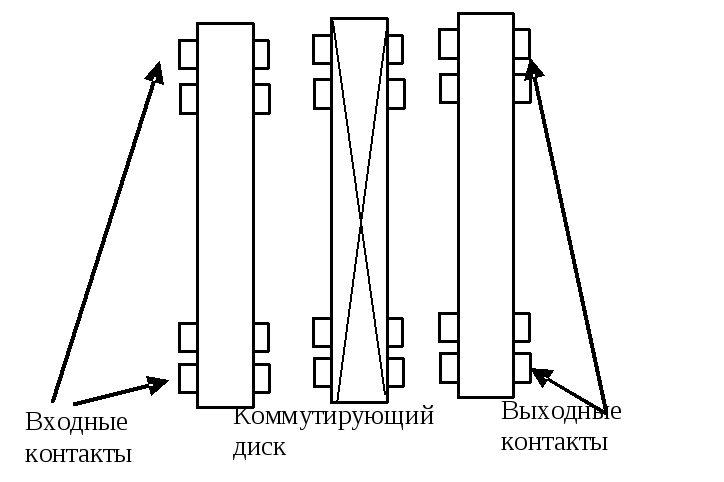
Рис.1.2.1. Дисковый шифратор

Криптосхему этого шифра можно представить в виде рис.1.2.2.

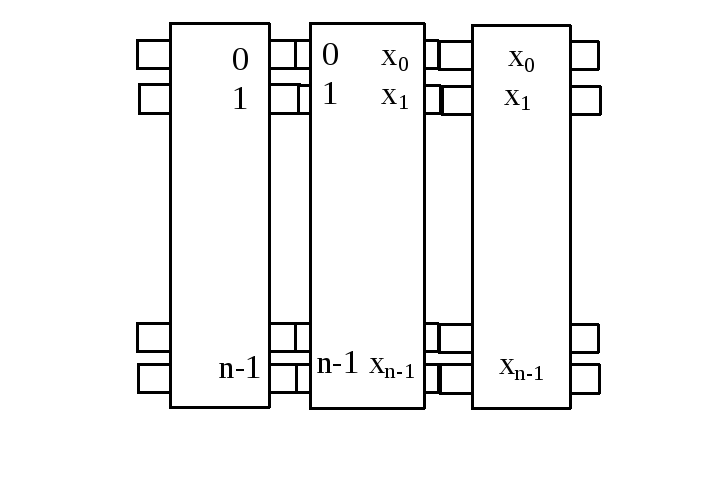
Рис. 1.2.2. Дисковый шифратор. Средний диск реализует подстановку

.

При повороте среднего диска на получаем рис. 1.2.3.

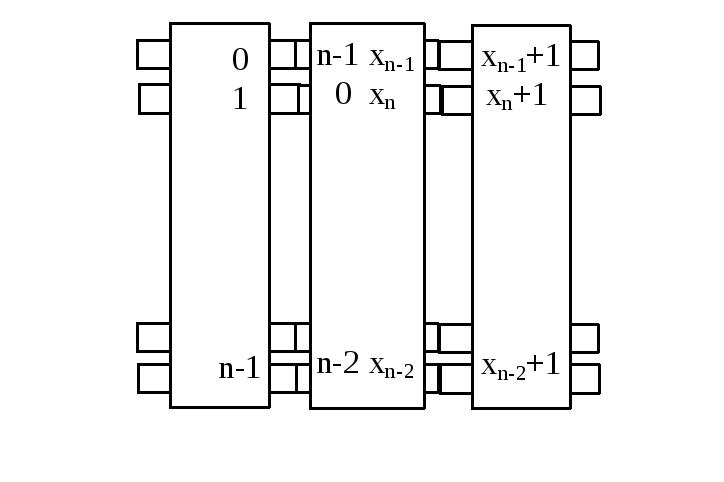
Рис. 1.2.3. Дисковый шифратор. Средний диск повёрнут на и реализует

Ту же подстановку относительно своих контактов

Если повернуть входной и выходной диски на  см. рис. 1.2.4.

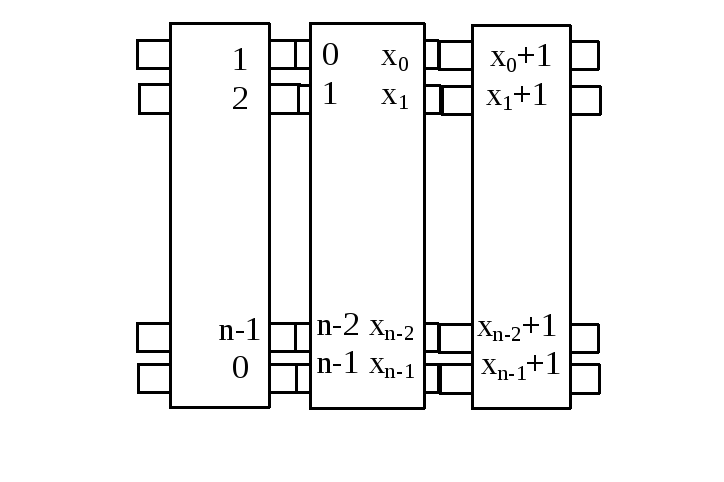
Рис. 1.2.4. Дисковый шифратор. Входной и выходной диски повёрнуты на  , средний диск реализует ту же подстановку относительно своих контактов. Это эквивалентно повороту среднего диска на.

Сравнивая положения дискового шифратора на рис. 2,3 можно увидеть, что при повороте среднего диска на дисковый шифратор реализует подстановку

,

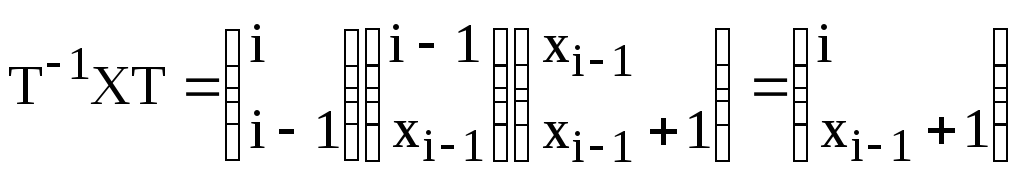где

.

При повороте среднего диска на , mдисковый шифратор реализует подстановку.

Если имеется N «средних» дисков, соединённых последовательно, реализующих подстановки X₁, X₂,…, X_N и повёрнутых относительно начального положения на , iто конструкция в целом реализует правило зашифрования

_j=.

Положения дисков в каждом такте могут изменяться в соответствии с законом движения дисков. Ключ k определен коммутациями (постановками) дисков, их расположением (порядком) на оси и их начальными угловыми положениями. В каждый такт работы дискового шифратора вырабатывается подстановка шифрования _j

Поточный шифр. Шифр поточной замены. Введем сначала вспомогательный шифр (I,Г,У,f) для шифрования букв алфавита I. Для ключа ₁Г, и буквы (открытого текста) iI шифрованный текст имеет вид f_1(i)=у. Обозначим через К – множество ключей поточного шифра. Для натурального числа L введем отображение Ф: КГ^L, для фиксированного ключа К положим Ф()=₁,₂,…,_L. Поточный шифр (I^L,К,F,У`) для вспомогательного шифра (Х=I,К=Г,У,f) шифрует открытый текст i₁,i₂,…,i_L на ключе К по правилу

F_(i₁,i₂,…,i_L)= f_1(i₁), f_2(i₂),…, f_L(i_L),

где f_(i)=f(i,).

Поточным шифром замены мы называем поточный шифр, для которого опорный шифр имеет вид (Х=I,К=Г,У=I,f), а (f_)_Г – семейство подстановок на I. Примерами поточных шифров служат шифры гаммирования, шифры простой замены. Поточный шифр с опорным шифром вида: I=К={1,2,…,n}, f(i, )=i+ mod |I| так же называют шифром гаммирования. При этом условно различают программный шифр гаммирования, в случае |К|<|I|^L, и случайный шифр гаммирования, в случае К=I^L, Ф – тождественное отображение.

Более общее понятие поточного шифра состоит в том, что в качестве множества открытых текстов рассматриваются все последовательности алфавита I длины не превосходящей некоторого L(0). Для шифрования текстов длины L используется гамма Ф_L()=₁,₂,…,_L. Таким образом, используются L функций Ф_j, j{1,…,L(0)}.