
илет1: Теорема об элементарных преобразованиях системы линейных уравнений.
Уравнение вида a1x1+a2x2+ …+anxn=b – линейное уравнение, где х1 х2…хn – неизвестные переменные, b – свободный член, а1 а1…аn – коэффициенты уравнения. Решение уравнения – совокупность чисел k1 k2…kn такая что, если подставить её в уравнение вместо неизвестных переменных, то получится верное числовое равенство. Система линейных уравнений: (1)
Элементарные преобразования системы линейных уравнений:
а)
2 уравнения системы (1) меняются местами
б) одно уравнение системы (1) умножается
на число
 ,
отличное от нуля в) к уравнению системы
(1) прибавляется другое уравнение,
умноженное на число
,
отличное от нуля в) к уравнению системы
(1) прибавляется другое уравнение,
умноженное на число
Если система линейных уравнений не имеет решений, то она несовместная, если имеет – совместная. Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, если каждое решение одной системы уравнений является решением и другой системы, или они несовместны. Теорема об элементарных преобразованиях системы линейных уравнений:
При любом элементарном преобразовании системы лин. уравнений получается система уравнений, эквивалентная данной
Доказательство:
очевидно, что при преобразовании (а)
получается система, эквивалентная
данной выполним преобразование (б).
i-тое
уравнение системы (1) умножить на число
 ,
отличное от нуля.
,
отличное от нуля.
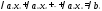 - i-тое
уравнение системы(2), все остальные
уравнения, как в (1)
- i-тое
уравнение системы(2), все остальные
уравнения, как в (1)
Пусть
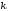 ,
,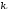 ,…,
,…,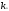 -
решения системы (1), в том числеi-того
уравнения системы (1)
-
решения системы (1), в том числеi-того
уравнения системы (1)
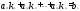 подставим эти же
числа
подставим эти же
числа
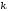 ,
,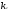 ,…,
,…,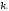 в левую частьi-того
уравнения системы (2)
в левую частьi-того
уравнения системы (2)
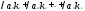 =
=
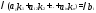
Набор
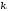 ,
,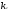 ,…,
,…,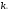 является решениемi-того
уравнения системы (2), а значит и решением
системы (2), поскольку все остальные
уравнения в (2) такие же как в системе
(1). Так как
является решениемi-того
уравнения системы (2), а значит и решением
системы (2), поскольку все остальные
уравнения в (2) такие же как в системе
(1). Так как
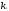 ,
,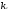 ,…,
,…,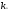 -произвольные
решения системы (1), то всякое решение
системы (1) является решением системы
(2)
-произвольные
решения системы (1), то всякое решение
системы (1) является решением системы
(2)
Заметим,
что систему (1) можно получить из системы
(2) также при помощи преобразования (б).
для этого нужно i-тое
уравнение системы (1) умножить на число
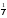 .
В соответствии с доказанным всякое
решение системы (2) будет решением (1)
.
В соответствии с доказанным всякое
решение системы (2) будет решением (1)
выполним
преобразование (в). К i-тому
уравнению системы (1) прибавим j-тое
уравнение
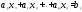 (3) , умноженное на число
(3) , умноженное на число .
Преобразованное в системе (3)j-тое
уравнение будет таким
.
Преобразованное в системе (3)j-тое
уравнение будет таким
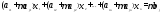
Пусть
 ,
,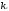 ,…,
,…,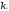 -произвольные
решения системы (1), в том числеi-того
и j-того
уравнения
-произвольные
решения системы (1), в том числеi-того
и j-того
уравнения
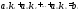 ,
,
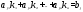
Подставим этот же набор чисел вместо неизвестных в левую часть j-того уравнения (3)
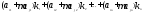 =
=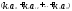 +
+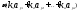 =
=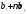 Это означает, что
Это означает, что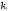 ,
,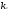 ,…,
,…,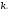 -
есть решениеi-того
уравнения системы (3) и всех остальных
уравнений, так как они такие же как как
в системе (1).
-
есть решениеi-того
уравнения системы (3) и всех остальных
уравнений, так как они такие же как как
в системе (1).
Билет2: Разрешение системы линейных уравнений по отдельной переменной.
При помощи элементарных преобразований системы линейных уравнений можно добиться того, что какое-либо неизвестной хk будет входить только в одно уравнение системы с коэффициентом, равным 1, а во всех остальных уравнениях отсутствовать (во все остальные уравнения неизвестное хk будет входить с коэффициентом 0). В таком случае системы линейных уравнений называется разрешенной относительно неизвестного хk , а неизвестное хk называется разрешенным. Система (1.2):
Разрешение системы (1.2) относительно неизвестного хk. Среди коэффициентов системы (1.2) выберем любой отличный от 0 коэффициент при неизвестной хk . Пусть это будет ask≠0. Будем называть ask коэффициентом, а уравнение с номером S (S-ое уравнение) – разрешающим. Выполним следующие элементарные преобразования системы (1.2):
1.Умножим
обе части разрешающего уравнения на
число
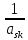 – элементарное преобразование 2. В
результате коэффициент при неизвестном
хk
станет равным 1 и уравнение примет вид:
– элементарное преобразование 2. В
результате коэффициент при неизвестном
хk
станет равным 1 и уравнение примет вид:
2.При
помощи уравнения (1.10) исключим неизвестное
хk
из всех остальных уравнений системы
(1.2). Чтобы исключить хk
из i-го
уравнения системы, умножим уравнение
(1.10) на (-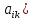 и сложим с i-ым
уравнением, то есть выполним элементарное
преобразование 3. В результате i-ое
уравнение не будет содержать неизвестную
хk:
и сложим с i-ым
уравнением, то есть выполним элементарное
преобразование 3. В результате i-ое
уравнение не будет содержать неизвестную
хk:
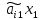 +
+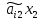 +…+0xk+…+
+…+0xk+…+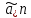 =
=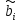
Чтобы
получить
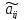 , надо
, надо
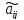 =
=
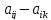
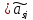 ,
j=
,
j=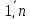 ,
j≠s
,
j≠s
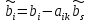 (1.11)
(1.11)
Точно также, как и для уравнения с номером i исключим хk из всех других уравнения системы (1.2). Получим окончательно систему уравнений:
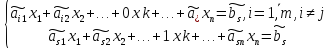 (1.12)
(1.12)
Система эквивалента исходной. В системе (1.12) неизвестное хk входит только в s-ое уравнение с коэффициентом 1 и отсутствует в других уравнениях. То есть система (1.12) является разрешенной относительно хk . Коэффициенты системы (1.12) и свободные члены уравнений кроме разрешающего вычисляются по формулам (1.11) , а для разрешающего – (1.10).
№3 Исследование и решение систем линейных уравнений методом Ж- Гаусса.
Сущность метода Ж- Гаусса заключается в том, что при нахождении конечного числа элементарных преобразований система линейных уравнений преобразуется в эквивалентную- т.е разрешённую систему уравнений или эквивалентную ей несовместную систему. Процесс решений состоит из ряда последовательных этапов расчетов. После выполнения каждого этапа, система линейных уравнений становится разрешаемой относительно какого-либо неизвестного.
Процесс преобразований закончится в след. 2-х случаях:
1)мы придём к системе уравнений, содержащих уравнение вида 0=b, b≠0,тем самым установим несовместность исходной системы(1.2)
2)получим разрешённую систему уравнений ,эквивалентную системе (1.2) , очевидно число уравнений (r) в разрешенной системе ≤m-числа уравнений в системе (1.2) т.к в процессе преобразования мы отбросили уравнение 0=0…..r<n
r-число уравнений в разрешённой системе…. n-число неизвестных
*r=n т.е. система совместная и определённая, система уравнений имеет вид (1.13)
Система
(1.13) и равносильная ей (1.2) имеют
единственное решение(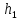 ,
,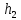 ,
,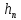 )-
совместная; определённая
)-
совместная; определённая
*r<n
разрешённая система имеет вид 1,14
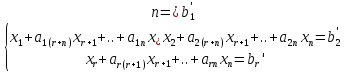 (1.14)
(1.14)
В
системе (1,14) неизвестные (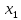 ,
,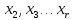 )
составляют наборразрешённых
неизвестных,
а остальные неизвестные- называются
свободными
неизвестными.
)
составляют наборразрешённых
неизвестных,
а остальные неизвестные- называются
свободными
неизвестными.
Возьмём
для свободных неизвестных произвольные
числовые значения
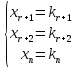 подставим их в систему (1.14) вместо
соответствующих неизвестных, найдём
значение для разрешённых (базисных)
неизвестных
подставим их в систему (1.14) вместо
соответствующих неизвестных, найдём
значение для разрешённых (базисных)
неизвестных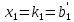 -
-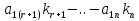
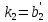 -
-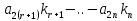
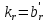 -
-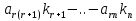
Легко
проверить, что набор чисел (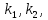
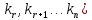 является решением системы (1.14)
→равносильной ей системы (1,2) т к
свободным неизвестным можно передавать
произвольное числовое значение, то
таким образом можно найти бесконечное
множество решений системы (1,2), в случаеr<n
система (1.2) является совместной,
но неопределённой.
является решением системы (1.14)
→равносильной ей системы (1,2) т к
свободным неизвестным можно передавать
произвольное числовое значение, то
таким образом можно найти бесконечное
множество решений системы (1,2), в случаеr<n
система (1.2) является совместной,
но неопределённой.
Каждое решение такой системы называется её частным решением, выраженным в базисных и неизвестных через свободные т.е. 1.15
Называется общим решением системы (1,2) и (1,14) среди частных решений. Выделим базисные, которые получаются при нулевых значениях всех свободных неизвестных.
Базисное
решение
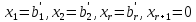
Из всего сказанного можно сделать выводы: система линейных уравнений будет несовместной, если при выполнении этапов преобразования по методу Ж- Гаусса мы получим противоречивое уравнение, если же такого уравнения нет, то система будет совместной.
Совместная система будет определённой, если она приводится к разрешённой системе в которой число уравнений равно числу неизвестных. И неопределённой, если в разрешённой системе число уравнений меньше числа неизвестных.
Следствие1! Если m<n, то система уравнений либо несовместная, либо неопределённая
Доказательство: Если система уравнений (1,2) является совместной, то она является определённой или неопределённой, это зависит от числа разрешённых в уравнении.
r≤ m ≤n, то система (1,2)- неопределённая .
Замечание1.Рассмотрим
систему линейных уравнений, в которой
свободные члены всех уравнений=0
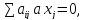 i=1,m
(1.16)
i=1,m
(1.16)
Такая система (1.16) называется системой линейных однородных уравнений. Эта система всегда совместна т к имеет тривиальное (нулевое) решение. Для системы (1,16) вопрос стоит в том, определённая она или не определённая. Система (1,16) является определённой, если она имеет только тривиальное решение и неопределённая, если кроме тривиального есть не нулевые.
Следствие2! m<n то система помимо нулевого имеет и ненулевое решение.
Замечание2
чтобы
записать систему (1,2) нужно знать
коэффициенты уравнений и свободные
члены. Выписываем их в виде таблицы.
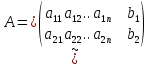
Получим
таблицу из чисел, которая содержит m
строк и n+1
столбцы. Всякая прямоугольная таблица
из чисел называется МАТРИЦЕЙ. Числа,
составляющие матрицу,- её Элементы.
Элементы одного n
столбца имеют 2 индекса.
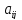
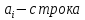
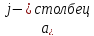
Матрица
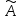 является расширенной матрицей системы
(1,2) она получается путём присоединения
к матрице из коэффициентов сист (1,2)
столбца свободных членов.
является расширенной матрицей системы
(1,2) она получается путём присоединения
к матрице из коэффициентов сист (1,2)
столбца свободных членов.
Билет 4: Определитель n-го порядка. Определение, свойство, устанавливающее равноправность строк и столбцов определителя, свойство о перестановке местами любых двух строк (столбцов) определителя (доказать).
Пусть дана квадратная матрица n-го порядка:1
Каждой квадратной матрице А можно поставить в соответствие число,вычисляемое по её элементам, называемое определителем или det.2
Если
в определителе (2) вычеркнуть i-ю
строчку и J-столбец,
на пересечении которых находится
элемент
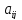 ,
то оставшиеся после вычёркивания
элементы определителя(2) n-го порядка
образуют определитель (n-1)-го порядка,
который называется минором элемента
,
то оставшиеся после вычёркивания
элементы определителя(2) n-го порядка
образуют определитель (n-1)-го порядка,
который называется минором элемента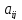 n-го
порядка
n-го
порядка
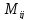 .
Число
.
Число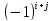 *
*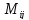 =
=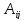 –алгебраическое дополнение элемента
–алгебраическое дополнение элемента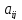 в определителе (2).
в определителе (2).
Определителем n-го порядка матрицы А называется число равное сумме произведений элементов 1ой строки определителя на их алгебраические дополнения:
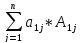 (3)
(3)
Формулу (3) будем называть формулой вычисления определителя n-го порядка разложения по элементам 1ой строки.
Такая
замена строк столбцами называется
транспонированием матрицы А. Матрица
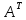 - транспонированная матрица. Определитель
матрицы
- транспонированная матрица. Определитель
матрицы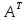 получается транспонированием определителя
матрицы А.
получается транспонированием определителя
матрицы А.
Свойство 1: определитель не меняется при транспонировании ( устанавливает равноправность строк и столбцов).
detA
= det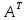
Любое утверждение, высказанное относительно строк, справедливо и для столбцов.
Свойство2: при перестановке местами любых 2х строк или столбцов определителя знак определителя меняется на противоположный.
Док-во: докажем свойство методом математической индукции. Для определителя 2-го порядка свойство выполняется :
Будем считать, что свойство справедливо и для определителя (n-1)-го порядка. Докажем, что оно справедливо и для определителя n-го порядка.
Пусть
в определителе (2) меняются i-я и k-я
строки,а остальные остаются на месте.
При этом i
 1 k
1 k
 1
1
detA’
=
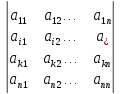 (6)
(6)
Разложим определитель (6) по элементам 1ой строки:
detA’
=
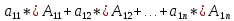
При
этом
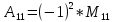
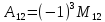
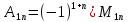
Все миноры определителя (6) отличаются от соответствующих миноров определителя (2) тем, что в них поменялись i-я и k-я строчки. Так как все эти миноры являются определителями (n-1)-го пордяка, то на основании индуктивного предположения знак их изменится на противоположный. Поэтому изменится знак у всех алгебраических дополнений элементов 1ой строки, и мы в итоге получим, что : detA’ = - detA
Пусть
в определителе (2) переставляется 1я
строка с любой другой строкой i
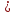 1 K
1 K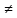 1
1
А все остальные строки остаются на месте. Мы получим определитель (6). Для вычисления определителя (6) используем формулу (3). И в этом случае все алгебраические дополнения элементов 1-го столбца определителя (6) отличаются знаком от соответствующих алгебраических дополнений определителя (2). Следовательно: detA’= - detA
Билет5: Доказать, что определитель n-го порядка равен сумме произведений любой его строки (столбца) на их алгебраические дополнения.
Опр-ль n-ного порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения.
Док-во: возьмем любую i-ую строку опр-ля (1) и докажем справедливость формулы (2):
det
А=
 (2) det A= ai1Ai1
+ai2Ai2+…+ainAin
(2)
(2) det A= ai1Ai1
+ai2Ai2+…+ainAin
(2)
Переместим i-ую строку на 1ое место, не меняя взаимного расположения остальных строк. В рез-те получим опр-ль:
det
А’’=
 (3)
(3)
Чтобы прийти к опр-лю (3) нужно поменять i-ую строку с (i-1)ой строкой, затем с (i-2)ой строкой и т.д… с 1ой строкой. Всего нужно произвести (i-1) перестановок строк. По св-ву: при перестановке местами любых 2х строк или столбцов опр-ля знак опр-ля меняется на противоположный - это приведет к изменению знака опр-ля (i-1) раз. Т.е.:
detA= (-1)i-1 detA” (4)
Запишем формулу для вычисления опр-ля (3) по элементам 1ой строки:
detA”=
ai1A11”
+ai2A12”+…+ainA1n”=
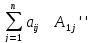 (5)
(5)
Причем А1j”= (-1)1+j М1j”= (-1)1+jMij ,т.к. элементы 1ой строки опр-ля (3) совпадают с элементами i-ой строки опр-ля (1), то М1j”=Mij
Теперь мы получаем:
detA”=
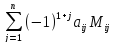 (6)
(6)
Подставим в формулу (4) detA” согласно (6)ой:
detA=
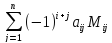 =
=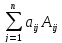
Таким образом формула (2) доказана и по свойству о равноправности строк и стобцов определителя доказана справедливость разложения опр-ля по любому его j-ому столбцу:
detA=
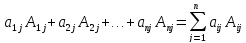 (7)
(7)
Билет 6: Доказать, что, если к элементам любой строчки (столбца) прибавить элементы любой другой строки (столбца), умноженные на любое число, то определитель не изменится.
Док-во:
A
=
 (1)detA
=
(1)detA
=
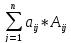 (2)
(2)
Прибавим
к элементам i-ой строки определителя
(2), элементы k-ой
строки умноженные на число
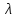 .
И разложим преобразованный определитель
по элементам i-ой строки:
.
И разложим преобразованный определитель
по элементам i-ой строки:
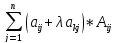 =
=
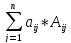 + λ
+ λ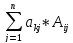 =
=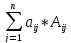
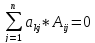 так как элементы
k-ой
строки умножается на алгебраические
дополнения элементов i-ой
строки (свойство определителя)
так как элементы
k-ой
строки умножается на алгебраические
дополнения элементов i-ой
строки (свойство определителя)
Замечание: это свойство позволяет любой строке или столбцу определителя заменить нулями все элементы кроме одного, тогда согласно формуле (2) вычисление определителя n-го порядк сведётся к вычислению определителя (n-1)-го порядка.
Билет7: Применение определителей к системе линейных уравнений.
Рассмотрим кв.систему линейных ур-ний:
а11х1+а12х2+…+а1nxn=b1 (1)
an1x1+an2x2+…+annxn=bn
det A= а11 а12 а1n
an1 an2 ann
Теорема 1 (Крамера): пусть кв. система лин. ур-ний (1) имеет отличный от нуля определитель D (D≠0), тогда сист.(1) является определенной – имеет единственное решение (k1, k2, …, kn) и решение находится по формуле kj=Dj/D . Dj – определитель, получаемый из определителя D заменой его j-столбца на столбец свободных членов сист.(1).
Теорема 2: Если система n-линейных однородных уравнений с n неизвестными имеет ненулевые решения, то определитель системы D=0.
Доказательство: Тк столбец свободных членов нулевой, то D1=D2=…=Dn=0, тк каждый такой определитель создает нулевой столбец kj=Dj/D. Если D≠0, то тогда решение (k1, k2, …, kn)=(0,0,…,0), по т.1(Крамера) решение единственное. Если D=0, система неопределенная и кроме тривиальных решений сущ. ненулевые решения. Система дает необх.условие существования ненулевых решений. D=0 кв.система однород.ур-ний имеет ненулевые решения.
Билет 8: Матрицы. Действия над матрицами и их свойства.
Всякая прямоугольная таблица из чисел называется матрицей. Числа,составляющие матрицу называется её элементами. Элементы имеют 2 индекса: 1.первый показывает номер строки 2. второй-номер столбца.
Матрица
А , содержащая m
– строк и n-столбцов
наз-ся матрицей вида mxn
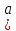 ij)
m,n
ij)
m,n
Матрица,
состоящая из одной строки, называется
строкой: А=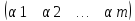 ,
а матрица, состоящая из одного столбца
– столбцом:
,
а матрица, состоящая из одного столбца
– столбцом:
Если
m=n
, то матрица наз-ся квадратной. Для
квадратной матрицы вводится понятие
– главная диагональ. Идет из левого
верхнего угла в правый нижний угол
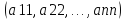 .
Квадратная матрица А называется
треугольной, если равны 0 все элементы
матрицы, расположенные выше или ниже
главной диагонали. Квадратная матрица,
у которой все элементы вне главной
диагонали =0 называется диагональной
матрицей:
.
Квадратная матрица А называется
треугольной, если равны 0 все элементы
матрицы, расположенные выше или ниже
главной диагонали. Квадратная матрица,
у которой все элементы вне главной
диагонали =0 называется диагональной
матрицей:
Диагональная матрица n-го порядка, у которой все элементы =1 называется единичной матрицей n-го порядка (E)
Матрица, все элементы кот =0 называется нулевой
Действия:
1.Суммой
2х матриц А и В одинакового размера mxn
называется матрица С того же размера
mxn,
элементы которой равны сумме одноименных
элементов матриц А и В:
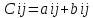 C=
A+B
C=
A+B
2.
Произведение матрицы на число. λ-какое-то
число А (a
ij)
m,n
– матрица. Произведением матрицы А на
λ(действительное число) называется
матрица С такого же размера как и А, в
которой:
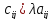
3.Умножение
матриц. Пусть имеется строка из m
элементов А=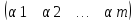 и столбец изn
элементов
и столбец изn
элементов
Произведением
2х таких матриц AxB
называется число, равное сумме
произведений соотвестствующей строки
и стобца:
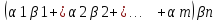
Св-ва(суммы матриц):
1.Переметительное(коммутативное): А+В=В+А
2.Сочетательное(ассоциативное): А+(В+С)=В+(А+С)=С+(В+А)
Св-ва(произведение матрицы на число):
1.Ассоциативное (сочетательное) относительно чисел множителя: λ*(MA)=(λM)A
2.Распределительное относит суммы матриц: λ (A+B)=λA +λ B
3.Распределительное относительно суммы чисел: (λ+M)=λA + AM
Св-ва (умножения):
1.Сочетательное: А* (BC)= (AB)*C
2.Распределительное (относительно суммы матриц): (A+B)*C=AC+BC
3.Переместительное (коммутативное) св-во в общем случае не выполняется. Порядок сомножителей существенен если взять множители в др. порядке, то произведение ьожет быть неопределенно:
Вопрос 9: Матричная форма записи системы линейных уравнений.
Пусть дана система m линейных уравнений с n неизвестными:
(1)
Выпишем матрицу, составленную из коэффициентов при неизвестных в системе (1)- матрица коэффициентов системы (1)
- матрица-столбец из неизвестных системы (1)
- матрица-столбец из свободных членов системы (1)
AX – существует
АХ имеет m строк и 1 столбец, - это матрица-столбец, элементы которого являются левые части уравнения (1)
АХ=В – матричная форма записи системы линейных уравнений
Билет 10
Билет13: N-мерное векторное пространство
N-мерным вектором называется упорядоченный набор из n чисел, записанный в виде строки или столбца: Число этих координат - размерность вектора.
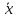 =
=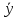
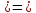 x1=y1,
x2=y2,
… , xn=yn
x1=y1,
x2=y2,
… , xn=yn
Линейные операции над N-мерными векторами:
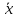 +
+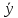 =(
x1+y1,
x2+y2,
… , xn+yn)
=(
x1+y1,
x2+y2,
… , xn+yn)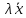 =(
λx1,
λx2,
… , xn)
=(
λx1,
λx2,
… , xn)
Введем
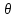 –
нулевой вектор( все координаты равны
0). Тогда
–
нулевой вектор( все координаты равны
0). Тогда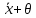 =
=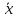
Для
каждого любого
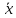 введем -
введем -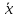 такой, что
такой, что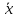 +
(-
+
(-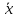 )=
)=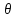
-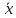 =-1*
=-1*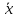 =(-x1,
-x2,
… , -xn)
=(-x1,
-x2,
… , -xn)
Свойства операций:
Переместительное (коммутативное)
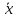 +
+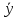 =
=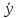 +
+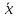
Ассоциативное (сочетательное)
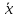 +(
+(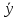 +
+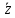 )=(
)=(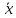 +
+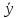 )+
)+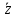
Ассоциативное свойство относительно числового множителя
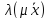 =
=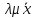
Распределительный (дистрибутивный) закон относительно суммы чисел
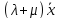 =
=
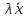 +
+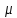
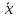
Распределительное (дистрибутивное) относительное суммы векторов:
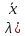 +
+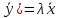 +
+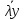
Множество
N-мерных
векторов
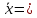 (x1,
x2,
… , xn),
в котором определены операции I
и II
над векторами со свойствами 1-5 называется
N-мерным
векторным или линейным пространством,
обозначается
(x1,
x2,
… , xn),
в котором определены операции I
и II
над векторами со свойствами 1-5 называется
N-мерным
векторным или линейным пространством,
обозначается
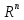 .
.
Линейными
пространствами являются множество
векторов в 3-х мерном пространстве на
плоскости и на прямой:
14. Векторная форма записи системы линейных уравнений.
Пусть дана система m линейных ур-ний с n неизвестными.1
Введем m-мерные векторы коэффициентов:
Каждая
координата
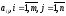 вектора
вектора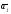 - коэффициент при неизвестной
- коэффициент при неизвестной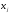 вi-ом
уравнение системы (1).
вi-ом
уравнение системы (1).
Введем вектор каждая координата, которого есть свободный член соответствующего уравнения.
Теперь систему (1) можно записать в виде векторного уравнения: (2)
Утверждение:
- решение
уравнения (2) тогда и только тогда, когда
 -
решение (1)
-
решение (1)
Док-во:1)
Пусть - решение уравнения (2). Подставим
 в
левую часть уравнения (2):
в
левую часть уравнения (2):
(3)
Вектор
(3)=вектору
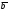 (из
(2)). Из равенства 2-х этих векторов следует
равенство для всехn
координат этих векторов:
(из
(2)). Из равенства 2-х этих векторов следует
равенство для всехn
координат этих векторов:
 (4)
(4)
Равенства (4) означают, что является решением системы (1).
2)
Пусть вектор
 является
решением системы (1), т.е. выполняется
равенства (4), которые равносильны
равенству 2-хn-мерных
векторов: вектора, записанного под (3)
и
является
решением системы (1), т.е. выполняется
равенства (4), которые равносильны
равенству 2-хn-мерных
векторов: вектора, записанного под (3)
и
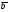 .
Т.е. получаем
.
Т.е. получаем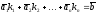 ,
откуда следует, что
,
откуда следует, что является
решением векторного уравнения (2),
которое будем называть системой линейных
уравнений.
является
решением векторного уравнения (2),
которое будем называть системой линейных
уравнений.
Билет15: Линейно зависимые и линейно независимые системы векторов и их свойства.
Пусть система векторов, -некоторые числа
Вектор
 =называется
линейной комбинацией, а коэффициенты
=называется
линейной комбинацией, а коэффициенты
 линейно
выражается через или вектор разлагается
по
линейно
выражается через или вектор разлагается
по
Набор чисел называется тривиальным, если все эти числа равны нулю. Если является тривиальным, то линейная комбинация векторов называется тривиальной
Если хотя бы одно из чисел отлично от нуля, то набор этих чисел называется нетривиальным.
Определение 1: система векторов называется л.з., если существует нетривиальные линейные комбинации векторов этой системы, равные нулю
Определение 2: система векторов называется л.н., если существует только тривиальная линейная комбинация этой системы, равная нулю.
Свойства: Теорема 1: если среди векторов есть хотя бы один нулевой вектор, то система л.з.
Доказательство:
пусть для определителя
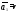 ,
,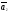 ,…,
,…,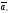 -любые
-любые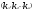 =
=
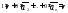 .
.
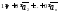 -нетривиальная
линейная комбинация
-нетривиальная
линейная комбинация система
векторов л.з.
система
векторов л.з.
Теорема 2: система векторов линейно зависима, и это равносильно тому, что хотя один из них является линейной комбинацией остальных векторов
Докажем
необходимость: известно, что
 ,
,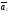 ,…,
,…,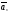 -л.з.
-л.з.
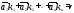 ,
,
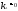 .
Обозначим -
.
Обозначим -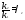 ,
-
,
-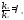 ,…,
-
,…,
-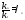
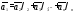

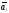 -линейная
комбинация остальных
-линейная
комбинация остальных
Докажем
достаточность: известно,
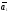 -линейная
комбинация остальных
-линейная
комбинация остальных
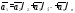
 -1
-1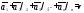
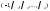 -нетривиальный
набор коэффициентов
-нетривиальный
набор коэффициентов
 линейная
комбинация нетривиальна, равная нулю
линейная
комбинация нетривиальна, равная нулю л.з.
л.з.
Теорема 3: если среди n-векторов какие-либо векторы л.з., то и все n-векторы – л.з.
Доказательство:
дано
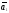 ,
,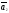 ,…,
,…,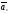 .
Пусть
.
Пусть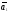 ,
, ,…,
,…,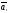 -л.з.
(s<n)
-л.з.
(s<n)
 существует
нетривиальная линейная комбинация
существует
нетривиальная линейная комбинация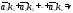 .
В левую часть допишем нулевые векторы
.
В левую часть допишем нулевые векторы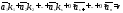 .
Линейная комбинация
.
Линейная комбинация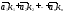 -нетривиальная,
т.к. существует неравный нулю коэффициент.
Так как линейная комбинация
-нетривиальная,
т.к. существует неравный нулю коэффициент.
Так как линейная комбинация -нетривиальна
-нетривиальна
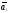 ,
,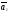 ,…,
,…,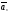 -л.з.
-л.з.
Теорема 4: если система n-векторов –л.н, то любая часть этой системы – л.н
Доказательство:
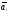 ,
,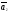 ,…,
,…,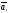 -любая
часть
-любая
часть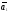 ,
,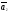 ,…,
,…,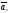 .
Предположим противное
.
Предположим противное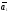 ,
,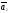 ,…,
,…,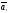 -л.з.
-л.з. по
теореме 3, все векторы
по
теореме 3, все векторы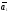 ,
,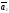 ,…,
,…,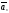 -л.з,
а это противоречит условию
-л.з,
а это противоречит условию
Билет 16. Базис системы векторов. Теорема о единственности разложения каждого вектора системы по базису этой системы.
Базисом системы вектора a1,a2..an называется такая часть этой системы векторов ai1,ai2..air для которой выполняются 2 условия:
1)ai1,ai2..air - л.н.
2)любой вектор данной системы разлагается по векторам ai1, ai2..air.
Теорема: Коэффициенты разложения каждого вектора системы по базису этой системы определяется единственным образом.
Док-во: Пусть существует 2 разложения вектора aj по базису ai1…air , то есть
Aj = k1ai1+k2ai2+..krair. (1)
Затем записываем это же выражение, только везде над k волнистые линии.(2)
Значит, наборы коэффициентов различны.
Вычтем из (1) (2)
θ= (k1-k1 c волной)ai1 +(k2-k2 c волной)ai2 +…+(kr-kr c волной)ai2 –линейная комбинация ai1, ai2…air.
Только тривиальная линейная комбинация этих векторов равна нулевому вектору, значит все коэффициенты K=0, т.е
k1=k1 c волной
k2=k2 c волной
kr=kr с волной
Эти, единственным образом определяемые коэффициенты разложения вектора системы по базису сист. векторов называются координатами вектора в этом базисе.
Билет
17. Примеры базисов линейных пространств.
Доказать, что система единичных векторов
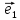 ,
,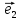 ,
…,
,
…,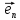 пространства
пространства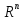 служит базисом этого пространства.
служит базисом этого пространства.
R2 –базис включает 2 неколлинеарных вектора.
R3- базис включает 2 некомпланарных вектора.
Rn- докажем, что в Rn базис образует система единичных векторов e1(1,0,0,0) ,e2(0,1,0,0) …en(0,0,0…1).
1) У каждого вектора ei этой системы векторов все координаты =0, кроме i-той координаты=1.
k1e1+k2e2+…+knen=k1(1,0..0) +k2(0,1…0)..+kn( 0,0,…1)=(k1,k2…kn) –линейная комбинация k1e1+knen= θ, значит (k1,k2…kn)= θ, то есть k1=0,k2=0..kn=0.
Только тривиальная линейная комбинация системы единичных векторов равна нулевому вектору.
2)Каждый вектор ā1,ā2…ān можно представить в виде:
āᵣ=
a1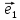 +
a2
+
a2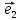 +…+an
+…+an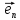 =
a1
(1,0…0)+ a2
(0,1,0…0)+…+an(0…0)=( a1,
a2…an)
=
a1
(1,0…0)+ a2
(0,1,0…0)+…+an(0…0)=( a1,
a2…an)
Доказали
2 условия,значит система единичных
векторов – базис
18. Доказать теорему: базис системы векторов есть максимальная линейно независимая часть этой системы.
Пусть ai1, ai2, …, air – базис системы векторов a1, a2,…,an.
Добавим любой aj из данной системы. Получим ai1, ai2, …, air, aj. По определению базиса, любой вектор данной системы векторов разлагается по базису: aj=k1ai1+k2ai2+…+krair. По теореме: система векторов является л.з. если хотя бы 1 из них является линейной комбинацией остальных векторов)=> ai1, ai2, …, air, aj – л.з.=> ai1, ai2, …, air – max л.н.часть.
Следствие:
В любой n-мерной системе векторов не может быть больше чем n линейно независимых.
Док-во:
В
пространстве
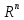 есть базис из n единичных векторов.
Согласно теореме любая система из n+1
векторов в
есть базис из n единичных векторов.
Согласно теореме любая система из n+1
векторов в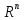 линейно зависима.
линейно зависима.
