Высшая математика экзамен

1.Векторы. Линейные операции над ними. Длина векторов. Проекция вектора на ось.

Вектор - вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат. Линейными операциями над векторами называется сложение и умножение на число. Линейные операции: сложение вектора, умножение вектора на число. Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка. Проекцией вектора на ось L называется число равное модулю вектора , если он правоориентированный на оси L или противоположное ему число в противном случае. Условие коллинеарности (параллельности или совпадения) векторов.

2. Задание вектора в декартовой системе координат. Длина вектора. Проекция вектора на координатную ось. Деление вектора в заданном отношении. Условия параллельности и перпендикулярности векторов. Декартовая система координат – прямоугольная. Для задания декартовой прямоугольной системы координат выбирают взаимно перпендикулярные прямые, называемые осями. Точка пересечения осей O называется началом координат. На каждой оси задается положительное направление и выбирается единица масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P. Декартовыми прямоугольными координатами точки P на плоскости в двухмерной системе координат называются взятые с определенным знаком расстояния этой точки до двух взаимно перпендикулярных прямых — осей координат или проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси. Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния)этой точки до трех взаимно перпендикулярных координатных плоскостей или проекции радиус-вектора r точки Р на три взаимно перпендикулярные координатные оси. Проекция вектора а на ось равна произведению модуля вектора а на косинус угла между вектором и осью. Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов

3. Скалярное произведение и его свойства. Угол между векторами. Скалярным произведением в линейном пространстве называется функция , принимающая числовые значения, определенная для каждой пары элементов и удовлетворяющая следующим условиям: 1. для любых трех элементов и пространства и любых чисел справедливо равенство ; 2. для любых и справедливо равенство ,где черта означает комплексное сопряжение; 3. для любого имеем , причем только при . . Угол между векторами, , дается формулой , или в координатах.  Свойства скалярного произведения:

5. Векторное произведение и свойства. Площади параллелограмма и треугольника. Векторным произведением вектора а на вектор b называется вектор с, который: 1. Перпендикулярен векторам a и b, т. е. с^а и с^b; 2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е. 3.Векторы a, b и с образуют правую тройку. Свойства векторного произведения: 1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19). Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , bxa противоположной ориентации). Стало быть axb = -(bxa ). 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l(а хb ) = (lа ) х b = а х (lb ). Согласно определению векторного произведения векторов а и b |а хb | = |а| * |b |sing , т. е. S _пар = |а х b |. И, значит, DS =1/2|а х b |.

6. Векторное произведение векторов в декартовой системе координат. Площади параллелограмма и треугольника. Мы будем использовать таблицу векторного произведения векторов i , j и k :если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус». Пусть заданы два вектора а=а_хi +a_yj +a_zk и b =b_xi +b_yj +b_zk . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

7. Смешанное векторное произведение. Условие компланарности трех векторов. Вычисление объема пирамиды, построенной на трех векторах. Смешанным произведением трех векторов , , называется число, равное векторному произведению , умноженному скалярно на вектор , то есть . Имеет место тождество, ввиду чего для обозначения смешанного произведения употребляется более простой символ . Таким образом, , . Условие компланарности: один из векторов – нулевой, два из векторов – компланарны, линейная зависимость для тройки векторов определяет компланарность этой тройки согласно тому, что компланарность сама по себе и есть такая линейная зависимость. Объем пирамиды равен одной шестой объема параллелепипеда, построенного на

его сходящихся в одной вершине ребрах. А объем этого параллелепипеда – абсолютная

величина смешанного произведения трех векторов, общее начало которых находится в

одной из вершин пирамиды, а концы – в остальных трех ее вершинах. Если вершинами

пирамиды служат точки M1, M2, M3, M4, то полагая a=M1M2; b=M1M3; c=M1M4, получим V=1/6[abc].

8. Прямая на плоскости и виды ее задания. Исследование общего вида уравнения прямой. Уравнение пучка прямых. Общее уравнение Ax + By + C ( > 0). Частные случаи: 1) By + C = 0 - прямая параллельна оси Ox;2) Ax + C = 0 - прямая параллельна оси Oy;3) Ax + By = 0 - прямая проходит через начало координат; 4) y = 0 - ось Ox; 5) x = 0 - ось Oy. Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром в S. Если и - уравнения двух прямых, пересекающихся в точке S, то уравнение , где , - какие угодно числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S. Более того, в уравнении (1) числа , всегда возможно подобрать так, чтобы оно определило любую (заранее назначенную) прямую, проходящую через точку S, иначе говоря, любую прямую пучка с центром S. Поэтому уравнение вида (1) называется уравнением пучка (с центром в S). Уравнение пучка прямых .

9. Угол между прямыми на плоскости. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой. Если заданы две прямые y = k₁x + b₁,  y = k₂x + b₂, то острый угол между этими прямыми будет определяться как . Две прямые параллельны, если k₁ = k₂. Две прямые перпендикулярны, если k₁ = -1/k₂. Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА,  В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают. Условия параллельности двух прямых: а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k₁ = k₂. б) Для случая, когда прямые заданы уравнениями в общем виде, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е. Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.   Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

            Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:. Координаты x₁ и у₁ могут быть найдены как решение системы уравнений: . Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0, то, решая, получим: . Подставляя эти выражения в уравнение, находим: .

10. Плоскость в пространстве и виды задания. Исследование общего вида. Возьмем 3 точки: , , , которые не лежат на одной прямой. Через них можно провести одну и только одну плоскость. Возьмем на этой плоскости любую точку . Построим 3 вектора . Т.к. они компланарны, то их смешанное произведение равно нулю: . В декартовых координатах: , , . - уравнение плоскости через 3 заданные точки. Пусть плоскость отсекает от осей отрезки . Т.е., плоскость проходит через 3 точки . Тогда уравнение этой плоскости будет иметь вид . . - уравнение плоскости в отрезках. Пусть плоскость задана в виде . . Или , где μ - вектор нормали. Пусть . Тогда уравнением плоскости будет . Т.к. , то . . - общее уравнение плоскости, где и - вектор нормали.

11. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей. Расстояние от точки до плоскости.    Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j₁ соотношением: j = j₁ или j = 180⁰ - j₁, т.е.

cosj = ±cosj₁. Определим угол j₁. Известно, что плоскости могут быть заданы соотношениями: , где(A₁, B₁, C₁), (A₂, B₂, C₂). Угол между векторами нормали найдем из их скалярного произведения . Таким образом, угол между плоскостями находится по формуле:. Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой. Условие перпендикулярности двух плоскостей: . Условие параллельности двух плоскостей: . Частные виды уравнений плоскости Пусть D=0, тогда плоскость проходит через начало координат. Если A=0, то плоскость параллельна оси Ox и аналогично для B=0 и C=0. Пусть задано уравнение . Поделим это уравнение на : . . . . Аналогично для b и c. Т.о., a,b,c - направляющие косинусы вектора нормали. - нормальное уравнение плоскости. Пусть плоскость задана уравнением и задана точка P. Тогда проекция вектора OP на вектор будет равна . Заметим, что расстояние от плоскости до точки P есть абслютная величина разности расстония от плокости до начала координат и проекции OP на . Т.е., расстояние от точки до плоскости есть , или .

12. Прямая в пространстве. Общий вид уравнения прямой. Каноническое уравнение прямой и угол между прямыми. Условия параллельности и перпендикулярности прямых.   Векторно-параметрическое уравнение прямой где - фиксированная точка, лежащая на прямой; - направляющий вектор. В координатах (параметрические уравнения): Канонические уравнения прямой Уравнения прямой по двум точкам  Прямая как линия пересечения двух плоскостей . Угол между двумя прямыми Необходимое и достаточное условие перпендикулярности двух прямых или Необходимое и достаточное условие параллельности прямой и плоскости или

13. Уравнение прямой, проходящей через две точки и уравнение прямой, заданной параметрически. Проекция точки на прямую. Расстояние между параллельными прямыми. Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M₁(x₁, y₁, z₁) и M₂(x_2, y₂, z₂), тогда уравнение прямой, проходящей через эти точки: . Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается: если х₁ ¹ х₂  и х = х₁, еслих₁ = х₂. Дробь = k называется угловым коэффициентом прямой. Параметрические уравнения , , . Найти проекцию точки М  на прямую  Составим уравнение плоскости, проходящей через точку М и перпендикулярной данной прямой. Направляющий вектор прямой  может служить вектором нормали к плоскости. Общий вид уравнения плоскости: Подставляем вместо  координаты вектора нормали, вместо   - координаты  точки . Получим: Отсюда Искомая плоскость: Точка пересечения данной прямой и полученной плоскости  будет проекцией точки М на данную прямую. отсюда .Координаты проекции:  Ответ:  Расстояние между двумя параллельными прямыми В координатах

14. Прямая и плоскость в пространстве. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. Проекция прямой на плоскость. Условия параллельности и перпендикулярности прямой и плоскости Рассмотрим прямую L: и плоскость α: Ax+By+Cz+D=0. Прямая L и плоскость α: а) перпендикулярны друг другу тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т. е. б) параллельны друг другу тогда и только тогда, когда векторы и перпендикулярны, т. е.и Am + Bn + Ср = 0. Угол между прямой и плоскостью. Угол α между нормальным вектором плоскости и направляющим вектором прямой вычисляется по формуле

15. Расстояние от точки до прямой в пространстве. Расстояние между скрещивающимися прямыми. Пусть в трехмерном пространстве заданы прямая, проходящая через точку M₀(x₀ y₀, z₀), параллельно вектору a = (l, m, n), и точка M₁(x₁ y₁, z₁), не лежащая на прямой. Расстояние h от точки M₁(x₁ y₁, z₁) до прямой может быть вычислено по формуле Расстояние h между скрещивающимися прямыми можно вычислить по формуле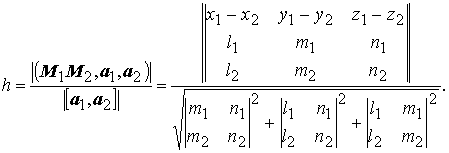

16. Уравнение окружности и эллипса и их исследование. Уравнение окружности ω ( A ;  R ) имеет вид ( x  –  a ) ²  + ( y  –  b ) ²  =  R ², где a и b – координаты центра A окружности ω ( A ;  R ) . Доказательство. Пусть задана окружность ω ( A ;  R ) на плоскости Oxy , где точка A , центр окружности – имеет координаты a  и b . По определению окружности для любой точки B  ( x ;  y ), лежащей на окружности ω ( A ;  R ), верно AB  =  R . Но в соответствии с теоремой 10.2   AB ²  = ( x  –  a ) ²  + ( y  –  b ) ². Таким образом, координаты x и y любой точки окружности ω ( A ;  R ) удовлетворяют уравнению ( x  –  a ) ²  + ( y  –  b ) ² = R ². Обратно: любая точка B  ( x ;  y ), координаты которой удовлетворяют уравнению, принадлежит окружности, так как расстояние от нее до точки A  ( a ;  b ) равно R . Отсюда по определению данное уравнение – уравнение окружности ω ( A ;  R ).  Пусть на плоскости заданы две точки и , и дано число a (a > c). Эллипс - множество точек M плоскости, для каждой из которых сумма расстояний от точек и равна 2a. Точки и называются фокусами эллипса; - большая ось; - малая ось; O - центр; - левый и правый фокусы; - вершины;- фокальные радиусы;Каноническое уравнение: Эксцентриситет: