16. Основные законы распределения непрерывной случайной величины: нормальный, логнормальный, равномерный, показательный.

Равномерный закон распределения.

Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке ab, если ее плотность вероятности φ(х) постоянна на этом отрезке и равно 0, вне его:

1/(b-a), a≤x≤b

0, x<a, x<b

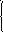
φ(х)=

1/(b-a)

Функция распределения равномерного распределения случайной величины:

0, при x≤a

(x-a)/(b-a)

1, x>b

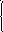
F(x) =

мат. ожидание равномерно распределенной случайной величины:

М(Х) = (a+b)/2

D(X) = (b-a)²/12

Равномерный закон распределения используется при анализе ошибок округления числовых расчетов, при стат. моделировании наблюдений, подчиняющегося заданному распределению.

Показательный закон распределения.

Непрерывная случайная величина Х имеет показательное распределение с параметром λ, если ее плотность вероятности имеет вид:

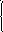λе^-х, х ≥0

φ(х)= 0, х < 0

λ

1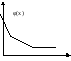

Функция распределения распределенная по показательному закону распределения имеет вид:

1-е^-λх, х ≥0

F(x) =

0, х<0

x 0 x

F(x) =∫φ(t)dt = ∫0 dt + ∫φ(t)dt = 1 - е^-λх

^{-∞ -∞ 0}

MX = 1/λ

DX = 1/ λ²

σ_x = √DX = MX = 1/λ

Найдем вероятность попадания случайной величины распределенной по показательному закону в (a;b)

P(a<x<b) = F(b) – F(a) = (1 - е^-λb)- (1 - е^-λa)

Показательное распределение используется в приложениях теории вероятностей, особенно в теории массового обслуживания, в физике, в теории надежности. Оно используется для описания случайных величин вида: длительность работы прибора до 1-го отказа; длительность времени обслуживания в системах массового обслуживания.

Нормальный закон распределения:

Закон Гаусса

Он является предельным законом, к кот. приближаются все остальные законы распределения.

Непрерывная случайная величина имеет закон Гаусса (Нормальный закон распределения) а и σ², если ее плотность распределения имеет вид:

-(x-a)²/2 σ²

φ_n(x) = 1/σ√2π e

Примеры: рост человека, дальность полета снаряда.

Кривая нормального распрежделения.

Нормальная кривая симметрична относительно прямой х=а, и имеет максимум в точке = 1/σ√2π и две точки перегиба

х = а +/- σ с ординатами 1/σ√2πе

Мат. ожидание нормальной случайной величины равно а .

МХ = а

DX = σ²

Выясним, как меняется нормальная кривая при изменении параметров:

Если σ – постоянная величина, меняется параметр а, т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы.

Если а – постоянная, меняется σ, то меняется ордината максимума.

При увеличении σ, ордината максимума уменьшается, но т.к. площадь под любой кривой распределения равна 1, кривая становится более плоской, растягиваясь вдоль оси абсцисс.

При уменьшении σ, нормальная кривая вытягивается вверх одновременно, сжимаясь с боков.

Таким образом, а, он же МХ, характеризует положение, а σ² – форму кривой.

Нормальный закон распределения с а = 0 и σ² = 1, называется стандартным или нормированным. Обозначается: N(0;1)

Сложность непосредственного нахождения функции распределения случайной величины, распределенной по

_+∞

нормальному закону распределения, по формуле: F(x) =∫φ(t)dt и вероятности ее попадания на интервал от а до b:

_b ^-∞

Р(а ≤ х ≤ b) = ∫φ(t)dt , связано с тем, что интеграл от функции F(x) является «неберущимся» в элементарных функции, и

^а

поэтому их выражают через интеграл вероятности или функцию Лапласа:

_х -t²/2

Ф(х) = 1/√2π∫e dt

⁰

Геометрически функция Лапласа представляет собой площадь фигуры под стандартной нормальной кривой на отрезке от (–х) до (х)

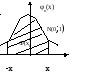
Функция распределения случайной величины Х, распределенной по нормальному закону распределению, выражается через функцию Лапласа:

FN(x) = ½ + Ф((х-а)/σ)

Геометрически функция распределения – это площадь под нормальной кривой на интервале от -∞ до х.

от -∞ до а; S=1/2

от а до х; S = Ф((х-а)/σ)

Свойства случайной величины, распределенной по нормальному закону распределения:

1. Вероятность попадания случайной величины на интервал от х₁ до х₂ равно приращению функции распределения на этом интервале:

Р(х₁ ≤Х≤ х₂) = F(х₁) – F(х₂) = [½ + Ф((х₁-а)/σ)] – [½ + Ф((х₂-а)/σ)] = Ф((х₂-а)/σ) - Ф((х₁-а)/σ) = Ф(t₂) – Ф(t₁)

t₁ = (х₁-а)/σ t₂ = х₂-а)/σ

2. Вероятность того, что отклонение случайной величины от мат. ожидания а не превысит положительную величину Δ по абсолютной величине равной значению функции Лапласа

Р(| Х-а | ≤ Δ) = 2Ф(t)

t=Δ/σ

Учитывая свойства нечетности, и свойство №1 можно эту формулу получить.

Р(-Δ≤х-а≤ Δ) = Р(а-Δ≤ х ≤а+ Δ) = Ф(а+ Δ) – Ф(а-Δ) = 2Ф(t)

Логнормальное распределение.

Непрерывная случайная величина имеет логнормальное распределение, если ее логарифм подчинен нормальному распределительному закону. Т.к. при всех положительных значениях Х неравенства равносильны, то функция распределения (Х<х lnX<lnx) логнормального распределения совпадает с функцией нормального распределения для СВ lnx, то есть

_lnx -(t - lna)²/ 2 σ²

F(x) = P(X< x) = P(lnX<lnx) =1/ σ√2π x∫ e dt

^∞

Дифференцируя по Х получим выражение для плотности вероятности для логнормального распределения:

-(lnx - lna)²/ 2 σ²

φ(х) =1/ σ√2π x e

Числовые характеристики СВ Х, распределенной по логнормальному закону имеют вид:

σ²/2

МХ = ае

σ² σ²

DX = а2е (е - 1 )

-х²

МоХ = ае

МеХ = а

*** Чем меньше σ, тем ближе друг к другу значения моды, медианы и мат. ожидания, а кривая распределения ближе к симметричной. Если при нормальном законе параметр а выступал в качестве среднего значения, то в логнормальном – в качестве медианы.

Логарифмическое распределение используют для описания распределения доходов, банковских вкладов, месячной з/п, долговечности изделий, в режиме износа и старения.