19. Плотность и функция распределения непрерывной двумерной случайной величины и их свойства.

Функцией распределения n-мерной случайной величины называется функция, выражающая вероятность совместного выполненияn неравенств , т.е.

Геометрически функция распределения двухмерной случайной величины означает вероятность попадания случайной точки (x;y) в заштрихованную область, расположенную левее и ниже точки M(x;y).

Квадрант

Правая и верхняя границы не включаются в квадрант – это означает, что функция распределения непрерывна слева по каждому из аргументов.

В случае дискретной двумерной случайной величины ее функция распределения определяется по формуле:

,

где суммирование вероятностей распространяется на все i, для которых , и всеj, для которых

Свойства функции распределения двумерной случайной величины:

1. Функция распределения 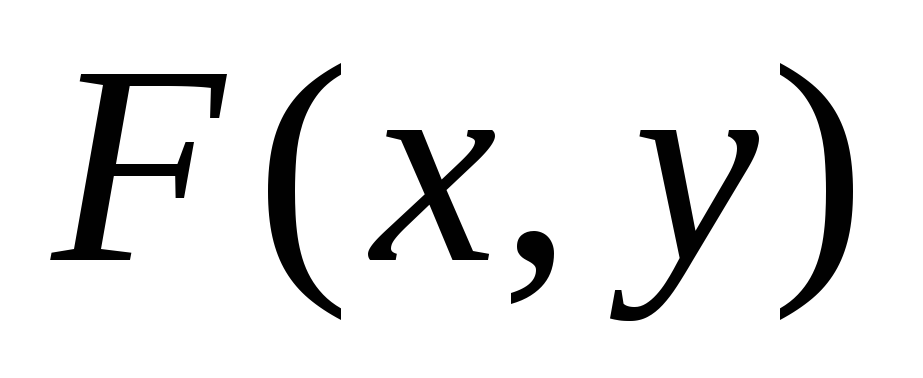есть неотрицательная функция, заключенная между нулем и единицей, т.е.

2. Функция распределения 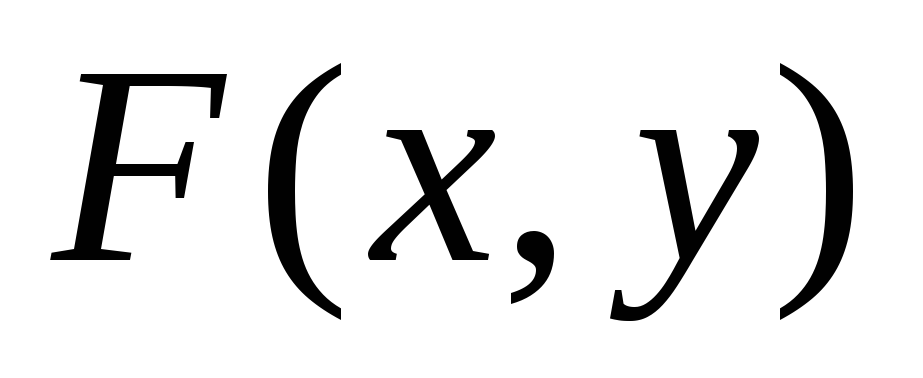есть неубывающая функция по каждому из аргументов, т.е.

при

при

3. Если хотя бы один из аргументов обращается в -∞, функция распределения F(x;y) равна нулю, т.е.

4. Если один из аргументов обращается в 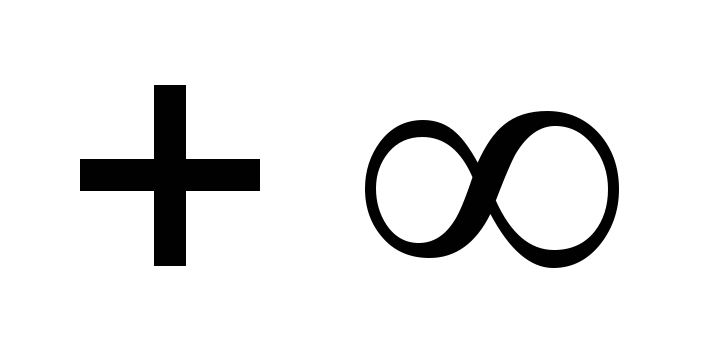, функция распределения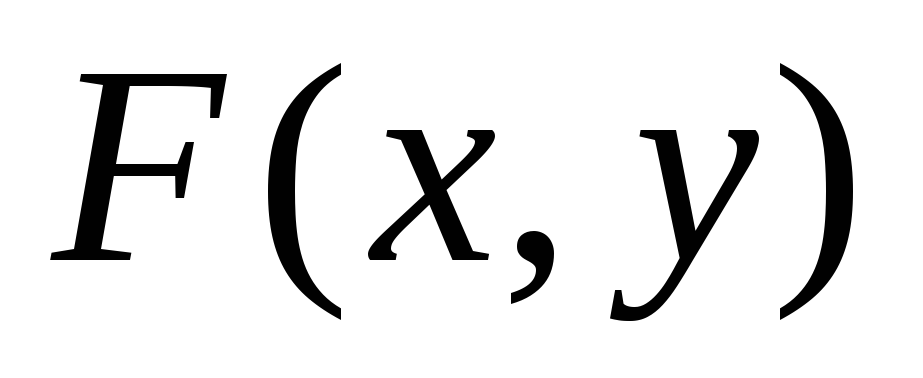становится равной функции распределения случайной величины, соответствующей другому аргументу:

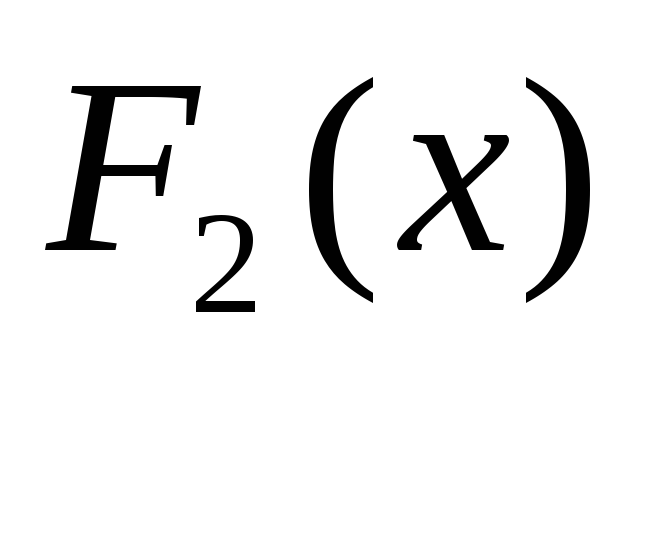где и- функции распределения случайных величинX и Y, т.е.

,

5. Если оба аргумента равны +, то функция распределения равна единице:

Геометрически функция распределения есть некоторая поверхность, обладающая указанными свойствами. Для дискретной случайной величины (X,Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции

Зная функцию распределения можно найти вероятность попадания случайной точки (X,Y) в пределы прямоугольника ABCD, т.е. .

A(x₁; y₂) B(x₂; y₂)

y₂

y₁

D(x₁; y₁) C(x₂; y₁)

x₁ x₂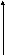

Плотность вероятности двумерной случайной величины.

Двумерная случайная величина (X,Y) называется непрерывной, если ее функция распределения F(x;y) – непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая смешанная производная .

Плотностью вероятности непрерывной двумерной случайной величины (X;Y) называется вторая смешанная частная производная ее функции распределения, т.е.

Геометрически плотность вероятности двумерной случайной величины (X,Y) представляет собой поверхность распределения в пространстве Oxyz.

Плотность вероятности обладает свойствами аналогичными свойствам плотности вероятности одномерной случайной величины.

Свойства плотности вероятности:

1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.

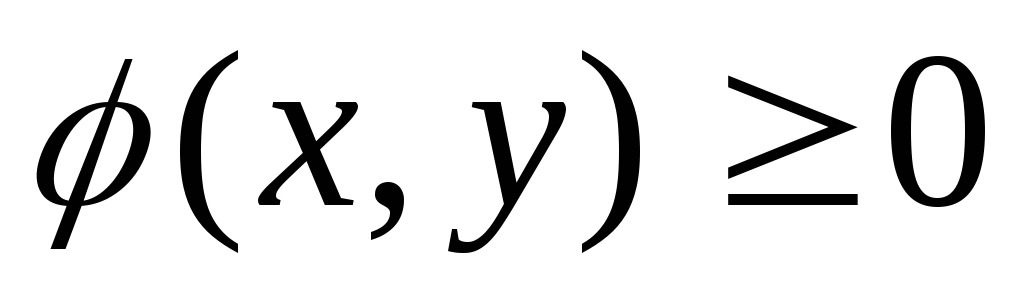
2. Вероятность попадания непрерывной двумерной случайной величины (X,Y) в область D равна

3. функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности 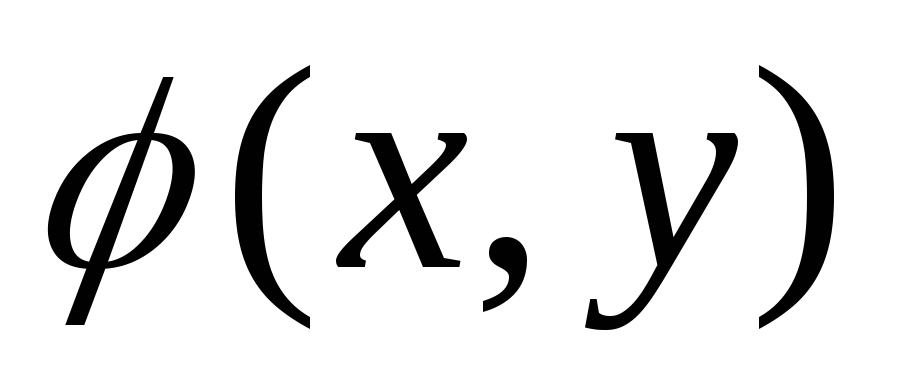по формуле:

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице.

Геометрически последнее свойство означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью Oxy, равен 1.

Замечание: Если имеется кривая распределения одномерной случайной величины, то конкретное значение ее плотности вероятности в данной точкеX определяется ординатой кривой

Если имеется распределение поверхности двухмерной случайной величины, то конкретное значение ее совместной плотности в данной точке (x,y) определяется геометрически аппликатой поверхности , а конкретное значение плотности вероятностиопределится геометрически площадью сечения поверхности. Плоскость параллельна плоскостиOyz и отсекает на оси OX отрезок x.