
- •СОДЕРЖАНИЕ
- •§ 1. Множества и операции над ними
- •2. Способы задания множеств
- •3. Операции над множествами
- •4. Свойства операций над множествами. Алгебра множеств
- •5. Декартово произведение множеств
- •§ 2. Отображения множеств
- •2. Произведение (композиция) отображений
- •3. Обратные отображения
- •§ 3. Отношения
- •2. Операции над бинарными отношениями и их свойства
- •§ 4. Отношения экивалентности
- •2. Отношения частичного порядка
- •§ 5. Комбинаторика
- •1. Размещения
- •2. Перестановки
- •3. Сочетания
- •4. Сочетания с повторениями
- •5. Бином Ньютона. Понятие о производящей функции
- •6. Числа Стирлинга
- •7. Число Белла
- •§ 6. Мощности множеств
- •2. Мощности бесконечных множеств. Счетные множества
- •4. Кардинальные числа. Гипотеза континуума
- •§ 7. Основные определения и типы графов
- •2. Основные типы графов
- •3. Обобщения понятия графа
- •4. Изоморфные графы
- •5. Количество различных графов порядка n
- •§ 8. Основные числовые характеристики и матрицы графа
- •2. Матрица смежности
- •3. Матрица Кирхгофа
- •4. Матрица инцидентности
- •§ 9. Подграфы и операции на графах
- •1. Подграфы
- •2. Операции над графами
- •§ 10. Связные графы и расстояние в графах
- •2. Компоненты связности. Связность графа и его дополнения
- •3. Расстояния на графах
- •§ 11. Деревья и остовы
- •1. Критерии дерева
- •2. Корневое дерево
- •3. Типы вершин дерева, радиус и центры
- •4. Остовы графа, циклический ранг и ранг разрезов
- •5. Задача о минимальном остове
- •7. Линейное пространство графа
- •§ 12. Эйлеровы и гамильтоновы графы
- •1. Эйлеровы графы
- •2. Гамильтоновы графы
- •§ 13. Планарные графы
- •2. Планарные графы. Формула Эйлера
- •3. Следствия из формулы Эйлера
- •4. Гомеоморфные графы. Критерий планарности
- •§ 14. Раскраски графов
- •2. Хроматическое число 2–дольного графа. Критерий 2-дольности
- •3. Некоторые оценки хроматического числа
- •4. Раскраски планарных графов
- •5. Реберная раскраска графа
- •§ 15. Паросочетания
- •1. Паросочетания
- •2. Теорема Холла о свадьбах
- •§ 16. Сети
- •1. Основные понятия
- •2. Потоки в сетях
- •3. Сетевое планирование
- •ТИПОВОЙ РАСЧЕТ «ГРАФЫ»
- •Задание
- •Варианты индивидуальных заданий
- •ЛИТЕРАТУРА
Множества A и B предполагаются непустыми. В противном случае, если A =
или B = , то A×B = . |
|
|
|
||
Если, например, |
A ={a1, a2}, |
B ={b1 , b2 , b3}, то: |
|||
|
A× B ={(a1, b1 ), (a1 , b2 ), (a1, b3 ), (a2 , b1 ), (a2 , b2 ), (a2 , b3 )} . |
||||
Вообще говоря, |
A × B ≠ B × A , |
за исключением случая, когда A = B . Тогда |
|||
произведение A × А называется декартовым квадратом множества A и обозначается: |
|||||
A2 . Если |
A = B = R – множество действительных чисел, |
||||
то R 2 ={(a, b) | a, b R} |
можно |
рассматривать, как |
|||
координатную плоскость, отождествив пару (a, b) с точкой, |
|||||
имеющей координаты x = a и y = b. |
|
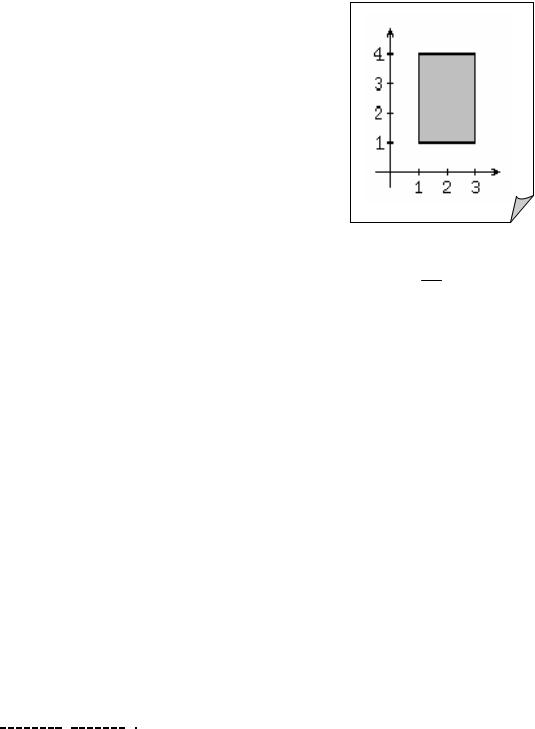
отрезки A = [1; 3], |
|||
В |
частности, |
если |
имеются |
||
B =[1; 4], |
то A × B представляет собой прямоугольник на |
||||
координатной плоскости xОy (рис. 1.3).
Всякая кривая Г на плоскости может быть истолкована как подмножество R2, определяемое
некоторым |
условием |
(уравнением): |
||
Г ={(x, y) R | f (x, y) = 0} . |
|
Рис. 1.3 |
|
|
Аналогично определяется декартовое произведение |
|
|
||
|
||||
любого количества непустых множеств. |
A1, A2, …, An. Тогда n-кой (кортежем) |
|||
Именно, |
пусть заданы множества |
|||
называется упорядоченный набор (a1, a2, …, an), такой что ai Ai i =1, n . Множество
всех таких n-ок называется декартовым произведением множеств |
A1, |
A2, |
…, |
An и |
|||
|
n |
|
|
|
n |
|
|
обозначается A1 × A2 ×K× An = ∏Ai . В частности, если все Ai = A , |
то |
∏Ai |
= An |
||||
|
i=1 |
|
|
|
i=1 |
|
|
называется n-ой декартовой степенью множества A. |
|
(R4 )3 |
|
|
|||
Замечание. |
Вообще говоря, (R 4 )3 ≠ R12 . |
Действительно, |
следует |
||||
рассматривать как |
множество матриц 3×4 , а R12 |
— кортежи, |
не |
учитывающие |
|||
матричной структуры.
Таким образом, уже из данного примера следует, что ассоциативный закон для декартового произведения множеств не выполняется.
Но дистрибутивные законы относительно , ∩ и \ имеют место:
(A1 A2 )× B = (A1 × B) (A2 × B);
(A1 ∩ A2 )× B = (A1 × B)∩(A2 × B);
(A1 \ A2 )× B = (A1 × B)\ (A2 × B).
В любом случае, операция “×” существенно отличается от предшествующих операций на множествах в том плане, что декартово произведение множеств из данного универсального множества U уже не принадлежит U.
§2. Отображения множеств
1.Основные понятия
Пусть X и Y – непустые множества. Если каждому элементу х Х ставится в соответствие единственный элемент y Y, то говорят, что задано отображение
10

множества Х во множество Y.
Часто не делают различий между понятием “отображение” и “функция”, однако функциями чаще всего называют отображения числовых множеств.
Если ƒ – отображение множества Х в Y, то пишут: ƒ: Х→Y или Х f →Y. Элемент y Y, который ставится в соответствие элементу х Х при отображении
ƒ:Х→Y, называется образом элемента х при отображении ƒ. При этом пишут: y = f(x) или ƒ:х ay. Элемент х в свою очередь называется прообразом y при отображении ƒ.
Определение 1. Два отображения ƒ:Х→Y и g:X→Y называются равными, если f (x)= g(x) для любого х Х.
Определение 2. Пусть задано отображение ƒ:Х→Y и А Х . Образом
множества А при отображении ƒ называется совокупность образов всех элементов множества А. Образ A обозначается: ƒ(А).
Итак, f (A)={f (x) |
|
x A}. Ясно, что |
f (A) f (X ). |
|
||||||
|
|
|||||||||
Определение 3. |
|
Пусть ƒ:Х→Y и |
А Х . Отображение, которое |
каждому |
||||||
элементу х А, рассматриваемому как элемент из Х, ставит в соответствие |
f (x) Y , |
|||||||||
называется сужением отображения ƒ на А и обозначается f |
|
A . |
|
|||||||
|
|
|||||||||
Таким образом, |
|
f |
|
A : A →Y , причём f |
|
A (x) = f (x) х А. Обратно, при |
||||
|
|
|
||||||||
выполнении этих условий ƒ: Х→Y является продолжением отображения f A : A →Y .
В случае, если Х и Y – конечные множества, то отображение ƒ:Х→Y может быть задано таблицей соответствий, состоящей из двух строк.
|
X ={x1 , x2 , x3 }, Y ={y1 , y2 } запись |
x |
x |
|
x |
|
|
||
Например, для |
|
1 |
|
2 |
|
3 |
|
||
f = |
|
y2 |
y1 |
|
|||||
означает, что f (x1 )= y1 , |
f (x2 )= y2 , |
f (x3 )= y1 . |
y1 |
|
|||||
|
|
|
|
|
|
|
|||
Упражнение: Выпишите все |
различные отображения |
ƒ:Х→Y |
в |
указанном |
|||||
примере и определите их количество. Найдите количество различных отображений
ƒ:Х→Y, если | X | = n, |
а |Y | = m. |
|
|
||||
Важным примером таких отображений служат подстановки из n элементов: |
|||||||
1 |
2 |
3 |
... |
n |
, где {δ1 |
|
,...,δn }= {1,2,...,n}. |
|
|
|
|
|
,δ2 |
||
|
δ2 |
δ3 |
... |
|
|||
δ1 |
δn |
|
|
|
|||
Другие примеры отображений:
-поворот плоскости вокруг начала координат на угол α;
-проецирование 3-мерного пространства на координатную плоскость xОy;
-ƒ:R→R, ƒ(x) = sin x.
Определение 4. Отображение ƒ:Х→Y называется инъективным (взаимно однозначным), если различным элементам множества Х соответствуют различные
образы из Y, т.е., если x1 ≠ x2 f (x1 )≠ f (x2 ).
Легко видеть, что это условие равносильно следующему: f (x1 )= f (x2 ) x1 = x2 .
Например, подстановки, повороты плоскости – взаимно однозначные
отображения; проецирование |
R 3 |
→ R 2 – |
не взаимно |
однозначное. |
Отображение |
|||||
f : R → R , где f (x)= sin x |
– не |
взаимно |
однозначное, |
но |
f |
|
π |
; |
π |
→ R , где |
: − |
2 |
|
||||||||
f (x)= sin x – взаимно однозначное. |
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|||
11

Определение 5. Отображение ƒ:Х→Y называется сюръективным, если каждый элемент y Y является образом для некоторого элемента х X, т.е. если каждый элемент
y Y имеет хотя бы один прообраз. |
|
|
|
f (X )=Y . |
|
||||
Понятно, что ƒ:Х→Y – сюръективно тогда и только тогда, когда |
|
||||||||
Например, подстановки, поворот на угол α, проецирование |
R 3 → R 2 – |
||||||||
сюръективны. |
Отображение f : R → R , где |
f (x)= sin x – |
не |
сюръективно, |
но |
||||
f : R → [−1; 1], |
f (x)= sin x – сюръективно. |
|
|
|
|
|
|
|
|
Определение 6. Отображение ƒ:Х→Y называется биективным, если оно |
|||||||||
одновременно и инъективно и сюръективно. |
|
|
|
π |
|
π |
|
|
|
Примеры. Подстановки; поворот |
на угол α; |
f : |
|
; |
|
]; |
|||
− |
2 |
2 |
→[−1;1 |
||||||
f (x)= sin x ; g : R → R, g(x)= 2x +1 – биективные отображения. |
|
|
|
|
|||||
|
|
|
|
|
|
||||
2. Произведение (композиция) отображений
Пусть ƒ: Х→Y, g : Y → Z и пусть х Х. Отображение ƒ переводит х в некоторый элемент y Y . При этом элемент y под действием отображения g переходит в некоторый элемент z из Z. Таким образом, в результате последовательного выполнения
сначала ƒ а потом g, каждый элемент х Х отображается в элемент |
z Z и мы |
получаем отображение h : X → Z . |
|
Определение 7. Произведением отображений ƒ:Х→Y и g : Y → Z |
называется |
отображение gf : X → Z определяемое равенством (gf )(x)= g(f (x)). |
|
Например, пусть f (x)= sin x , g(x)= 2x . Тогда (fg)(x)= sin(2x ), (gf )(x)= 2sin x . Отметим, что не всегда gf и fg определены одновременно. Для этого необходимо, чтобы g(Y ) X . В частности, если f : X → X , g : X → X , то gf и fg
определены. Но даже в этом случае равенство fg = gf, вообще говоря, не выполняется (это видно из рассмотренного примера), Таким образом, умножение отображений не коммутативно. Однако оно ассоциативно.
|
Теорема 1. Если ƒ:Х→Y, |
g :Y → Z , |
h : Z → U , то h(gf) и (hg)f определены и |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
равны. |
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Так |
как gf:X→Z, то h(gf):X→U. |
Аналогично, hg:Y→U, |
поэтому |
||||||||
(hg)f:X→U. Покажем, |
что х Х [h(gf )](x)=[(hg)f ](x). Пусть |
x0 X . |
Имеем: |
||||||||
f |
g |
h |
Поэтому |
согласно |
определению |
произведения |
|||||
x0 → y0 |
→ z0 →u0 . |
||||||||||
отображений [h(gf )](x0 )= h[(gf )(x0 )]= h[g(f (x0 ))]= h[g(y0 )]= h(z0 )= u0 и |
|
||||||||||
|
|
[(hg )f ](x0 )= hg(f (x0 ))= h(g(f (x0 )))= ...... = u0 . |
|
|
|||||||
|
Определение 8. Отображение f : X → X |
называется тождественным, или |
|||||||||
единичным, если f (x)= x , х Х. Обозначения: |
eX , |
1X, idX. |
|
|
|||||||
|
Теорема2. |
|
Если |
f : X → Y , то f eX = f и |
eY f |
= f . |
|
|
|||
|
|
|
|
||||||||
|
Следствие. |
Если f : X → X , то f eX |
= eX f = f . |
|
|
||||||
|
|
|
|
||||||||
Теорема 3. Пусть ƒ:Х→Y, g :Y →Z . Если ƒ и g инъективны, то fg – инъективно. Если ƒ и g сюръективны, то fg – сюръективно.
12
