4.2. Решение типового варианта контрольной работы n 2

Задача 2.1.Найти, если,,.

Решение.а). Дляимеем

.

б). Для .

.

в). Для .

.

Задача 2.2.Найти, если

Решение

а).

б). Дифференцируя уравнение для , имеем

,

откуда

.

Дифференцирование последнего соотношения дает

.

Внося выражение для , находим

.

в). Первая производная заданной параметрически функции вычисляется по формуле

.

Здесь

,

откуда

.

Вторую производную вычислим по формуле

.

Задача 2.3. Вычислить предел, пользуясь правилом Лопиталя:

.

Решение.а). Искомый предел является неопределённостью типа

По правилу Лопиталя

.

б). Предел является неопределённостью вида поэтому вначале его надо преобразовать к видуили:

.

К последнему (типа ) можно применять правило Лопиталя:

.

Полученный предел вновь является неопределенностью поэтому повторное применение правила дает

.

в). Предел является неопределенностью вида к которой удобно применять следующий прием. Обозначим

.

Тогда

. (1)

Вычислим вспомогательный предел

.

Искомый предел согласно (1) равен

.

Задача 2.4.Исследовать функцию и построить ее график.

Решение.Областью определения является вся действительная ось. Для отыскания участков монотонности находим

.

Тогда при(интервал возрастания),при(интервал убывания). Точкаявляется стационарной, посколькуПри переходе черезпроизводная меняет знак с плюса на минус, поэтому прифункция имеет локальный максимум.

Для отыскания участков выпуклости используется вторая производная

.

При илибудети функция вогнута; прии функция выпукла.

Вертикальных асимптот функция не имеет. Для отыскания наклонных асимптот вычислим

.

Поэтому при функция имеет асимптоту

Результаты исследования с учетом четности функции показаны на графике

Y

2

1

X

О

4.3. Решение типового варианта контрольной работы n 3

Задача 3.1.Найти градиент и уравнения касательной плоскости и нормали к заданной поверхностив точке.

.

Решение.Обозначим

Тогда

;

.

Величина градиента

.

Уравнение касательной плоскости, имеющей нормальный вектор (7,-4,-19) и проходящей через , запишется

,

или

.

Нормальная прямая имеет направляющий вектор (7,-4,-19) и проходит через , поэтому ее уравнения

.

Задача 3.2.Найти наибольшее и наименьшее значения функциив области D, ограниченной заданными линиями:

Решение.Область D показана на рисунке (треугольник OAB).

y

B(0,6)

D

1 С

0 2 A(3,0) x

Cтационарные точки являются решениями системы уравнений

,

откуда находим точку , принадлежащую, как видно из рисунка, области. В этой точке. (2)

Исследуем функцию на границе области D.

Отрезок ОА.ЗдесьиСтационарные точки определяются из уравненияоткудаВ этой точке

. (3)

На концах отрезка

, . (4)

Отрезок АВ.ЗдесьиИз уравнениянаходими

. (5)

При имеем

. (6)

Отрезок ОВ.ЗдесьПосколькуприфункция не имеет стационарных точек. Значения ее прибыли вычислены в (4), (6).

Из результатов (2)-(6) заключаем, что

причем наибольшее значение достигается в точке А(3,0), наименьшее - в точке С(2,1).

Задача 3.3.Найти полный дифференциал функции

Решение.Частные производные равны

Поэтому

.

Задача 3.4.Найти частные производные второго порядка функции

Решение.Сначала находим частные производные первого порядка:

Затем, дифференцируя найденные частные производные, получим частные

производные второго порядка данной функции:

Задача 3.5.Вычислить значение производной сложной функции

где

,

при с точностью до двух знаков после запятой.

Решение.Так как сложная функциязависит от одной переменнойчерез промежуточные переменныеи, которые в свою очередь зависят от одной переменнойто вычисляем полную производную этой функции по формуле

.

.

Вычислим ипри:

.

Подставим значения в выражение производной. Получим

.

4.4. Решение типового варианта контрольной работы № 4

Задача 4.1.С помощью интегрирования по частям вычислить неопределенный интеграл от функции вида

Решение. Поскольку

искомый интеграл равен

Задача 4.2.Вычислить неопределенный интеграл с помощью разложения на простейшие дроби подынтегральной функции

Решение.Поскольку степень многочлена в числителе не меньше степени знаменателя, следует выполнить деление:

.

Правильную дробь разложим на простейшие дроби

.

Методом неопределенных коэффициентов находим

,

откуда

.

Решая эту систему уравнений, имеем

.

Искомый интеграл равен

Задача 4.3.Вычислить с помощью подстановки неопределенный интеграл от функции.

Решение. Выполним подстановкуРазрешая уравнение относительно, находим:.

Тогда искомый интеграл запишется:

Разлагая подынтегральное выражениe на простейшие дроби

и раскрывая скобки в равенстве

,

приходим к соотношению

Система уравнений относительно запишется

Решая ее методом Гаусса, находим

Искомый интеграл равен:

.

Задача 4.4.Вычислить с помощью подстановки неопределенный интеграл от функции.

Решение. Универсальной является подстановкадля которой нетрудно проверить равенства

Поэтому искомый интеграл сводится к случаю интегрирования рациональной дроби

. (7)

Однако в ряде случаев более удобны подстановки:

(1) Тогда;

(2) Тогда;

(3) Тогда.

Подстановки 1,2 приводят к подынтегральным выражениям, содержащим радикал, и поэтому нецелесообразны. Для подстановки 3 приходим к интегралу, более простому, чем (7), и легко приводящемуся к табличному:

.

Задача 4.5.Вычислить площадь фигуры, ограниченной линиями:

а)

б)

Решение. а). Рассмотрим вспомогательную функциюна отрезкеПлощадь вычисляется по формуле

Исследуем Очевидно, чтоПоскольку

,

нетрудно проверить, что достигает в точкелокального минимума, причемКроме того,Поэтому наименьшее значениена [0,2], равное, положительно, и, значит,Имеем

Вычисляя интеграл по частям, находим

Поэтому

б). Здесь наИмеем, и, следовательно,меняет знак. Найдем интервалы, где она положительна или отрицательна. Отыскивая корни уравнениянаходим значениепоэтомуприиприИскомая площадь равна:

Вычисляем неопределенный интеграл

Тогда

Задача 4.6.Вычислить площадь, ограниченную кривойв полярной системе координат.

Решение. Кривая определена для тех значенийиз интервала(или), при которых выполняется условиеНеравенствоимеет решенияили

. (8)

Области (8) принадлежат интервалу при значенияхт.е.

Площадь вычисляется по формуле

Вычисляя неопределенный интеграл

находим

.

Задача 4.7. Вычислить несобственный интегралили доказать его расходимость.

Решение. Согласно определению несобственного интеграла с бесконечным пределом имеем

.

Поскольку корнями трехчлена в знаменателе будут то

.

Методом неопределенных коэффициентов находим , откудаПоэтому

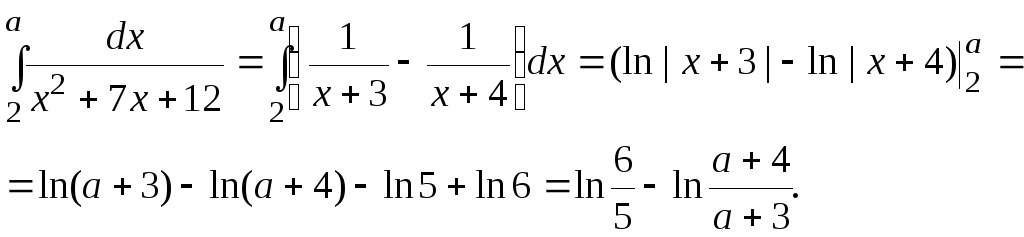
Значение несобственного интеграла равно

.

Задача 4.8.Вычислить массу неоднородной пластины, ограниченной заданными линиями и имеющей поверхностную плотность

D:

Решение. Вид области показан на рисунке.

Y

8

y=8x²

X

0 D 1

y= -x

-2

Масса пластины запишется с помощью двойного интеграла

.

Сведем двойной интеграл к повторному интегралу

Задача 4.9.Вычислить с помощью тройного интеграла объем области V, ограниченной указанными поверхностями: V: y=8-2x², z=0, y=0, x=0, z=2x+y.

Решение. Область V изображена на рисунке, где цифрами 1, 2 обозначены параболический цилиндр y=8-2x²и плоскость z=2x+y соответственно; остальные уравнения отвечают координатным плоскостям.

y

8 - B

V 2

1 4 -

D

S

0 C

Объем области посредством тройного интеграла запишется

Приведем интеграл к повторному

.

Через обозначены аппликаты точек(см. рис.), вычисленные из уравнений плоскостии плоскости, т.е.,. Черезобозначена область плоскости, на которую проецируется область. Поэтому при сведении двойного интеграла по области к повторному ординатыточеквычисляются из уравненияи уравнения линии, являющейся пересечением цилиндрической поверхностии плоскостит.е. уравненияИскомый объем равен

Задача 4.10.Вычислить: а) заряд проводника, располагающегося вдоль кривой, с плотностьюс помощью криволинейного интеграла первого рода;b) работу силывдоль траекторииLот т.Aдо т.Bс помощью криволинейного интеграла второго рода.

- четверть окружности между А(3,-3), В(5,-1). (2)- дуга параболыотА(0,1) доВ(1,-1).

Решение.а). Зарядqпроводника, имеющего плотность зарядавычисляется по формуле

.

(1). Окружность удобно задать в параметрическом виде:

.

Участку Lсоответствуют значения параметрагде

откуда Криволинейный интеграл выражается через определенный

причем верхний знак выбирается при и нижний - при

В данной задаче

(2). Для дуги параболы L удобнее использовать частный случай формулы при

Для имеем

Используем подстановку

Тогда

б). Работа силового поля с компонентамивдоль траектории АВ запишется

(1). Для четверти окружности приведем интеграл к определенному по формуле

(2). Для дуги параболы

Задача 4.11.Вычислить расход жидкости с полем скоростей, протекающей за единицу времени через частьплоскостилежащей в первом октанте. Единичная нормальнаправлена вне начала координат.

Решение.Искомый расход дан формулой

.

Единичная нормаль к плоскости имеет компоненты

.

Поверхностный интеграл можно выразить через двойной интеграл

,

где уравнение поверхности записано в явном виде:

.

Область является проекциейна плоскостьи ограничена линиями

.

Внося в двойной интеграл заданные функции, находим

.

Последний запишется через повторный интеграл

С о д е р ж а н и е

1.	Общие рекомендации студенту-заочнику по работе над курсом высшей математики . . . . . . . . . . . . . . . . . . . . . . . .		3
2.	Типовые программы курса «Высшая математика». Рекомендуемая литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		5
	2.1.	Программа курса «Высшая математика» для инженерных специальностей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	5
	2.2.	Программа курса «Высшая математика» для экономических специальностей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	12
3.	Контрольные работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		17
	3.1.	Правила оформления контрольных работ . . . . . . . . . . . . . . . . . . . . . . . .	17
	3.2.	Выбор варианта контрольной работы . . . . . . . . . . . . . . . . . . . . . . . . . . .	17
	3.3.	Задания контрольных работ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	18
	К о н т р о л ь н а я р а б о т а № 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		18
	К о н т р о л ь н а я р а б о т а № 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		34
	К о н т р о л ь н а я р а б о т а № 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		45
	К о н т р о л ь н а я р а б о т а № 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		51
4.	Примеры решения задач контрольных работ . . . . . . . . . . .		67
	4.1.	Решение типового варианта контрольной работы № 1 . . . . . . . . . . . . .	67
	4.2.	Решение типового варианта контрольной работы № 2 . . . . . . . . . . . . .	75
	4.3.	Решение типового варианта контрольной работы № 3 . . . . . . . . . . . . .	81
	4.4.	Решение типового варианта контрольной работы № 4 . . . . . . . . . . . . .	86