4. Примеры решения задач контрольных работ

4.1. Решение типового варианта контрольной работы №1

Задача 1.1. Дана система линейных неоднородных алгебраических уравнений

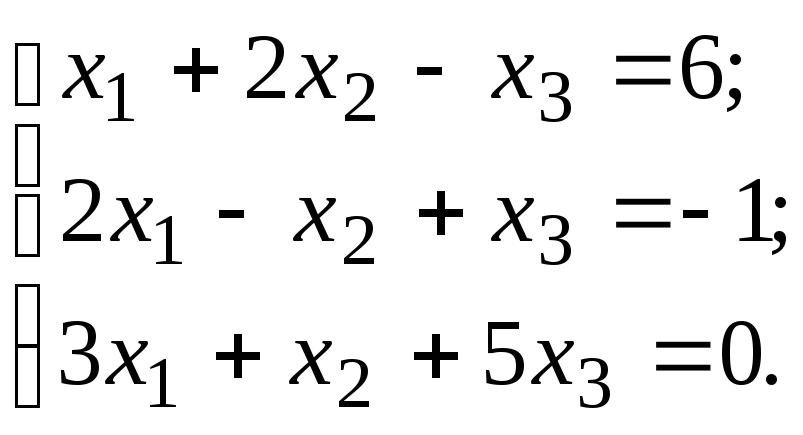
Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований расширенную матрицу приведем к трапециевидной форме

~ ~.

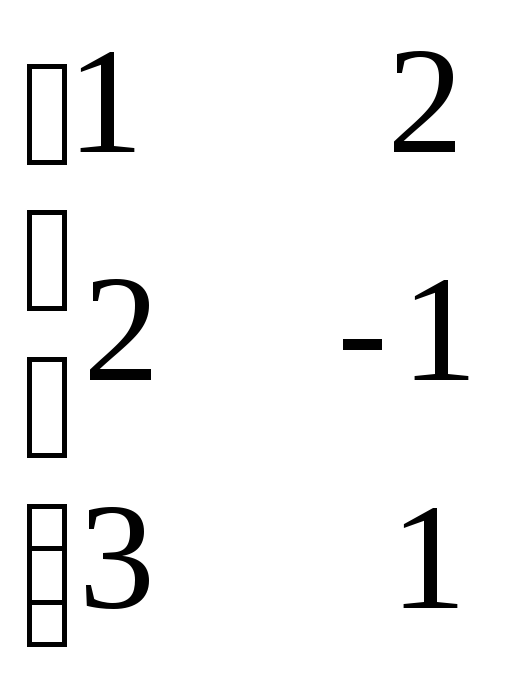
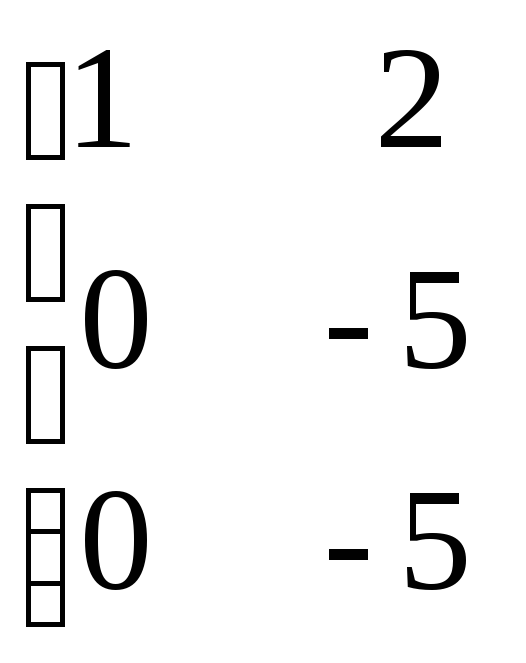
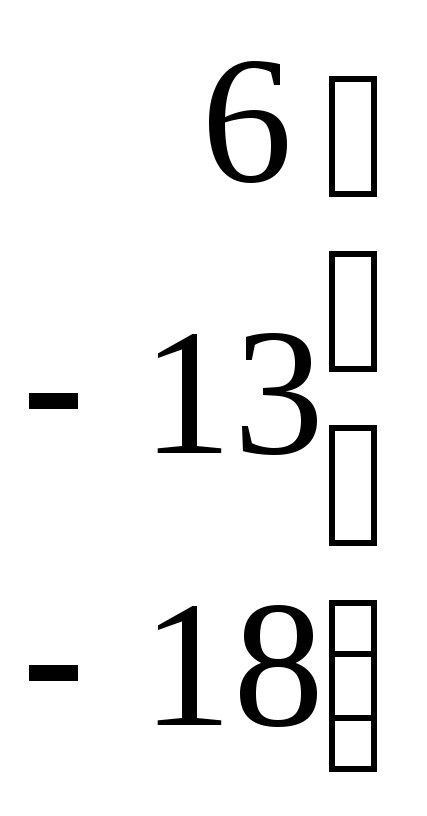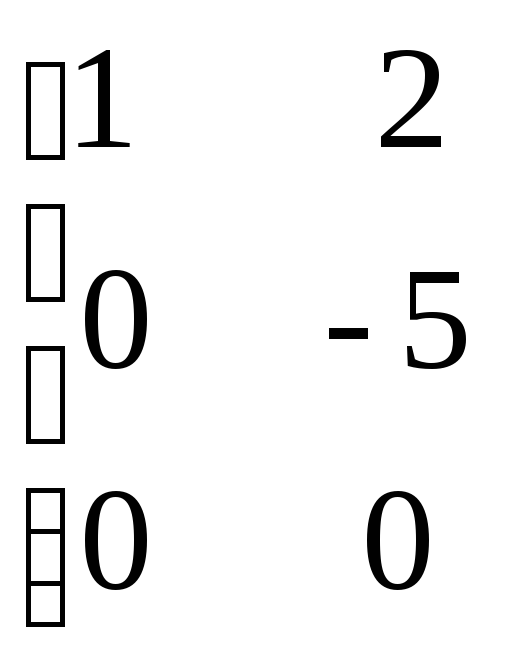
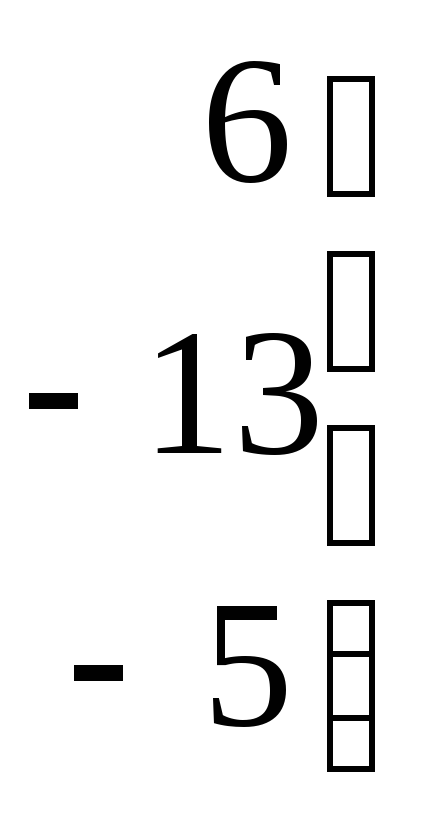Следовательно, (числу неизвестных системы). Значит, исходная система совместна и имеет единственное решение.

а). По формулам Крамера: где

.

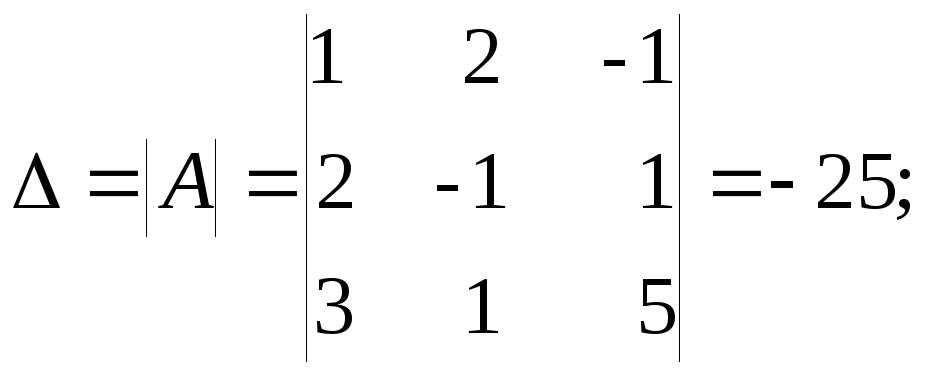
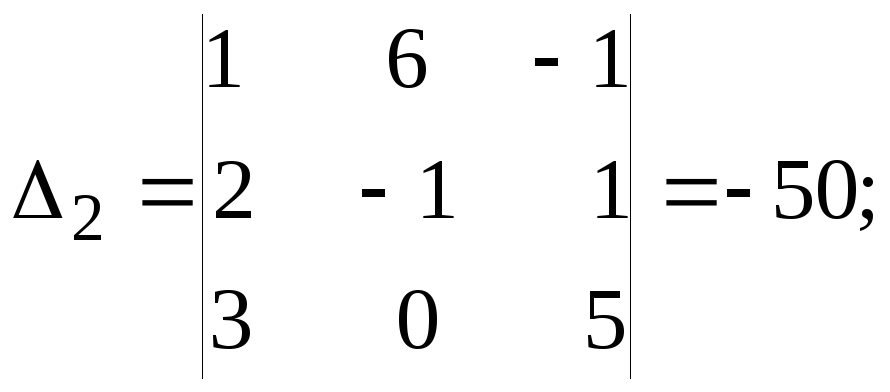
Находим .

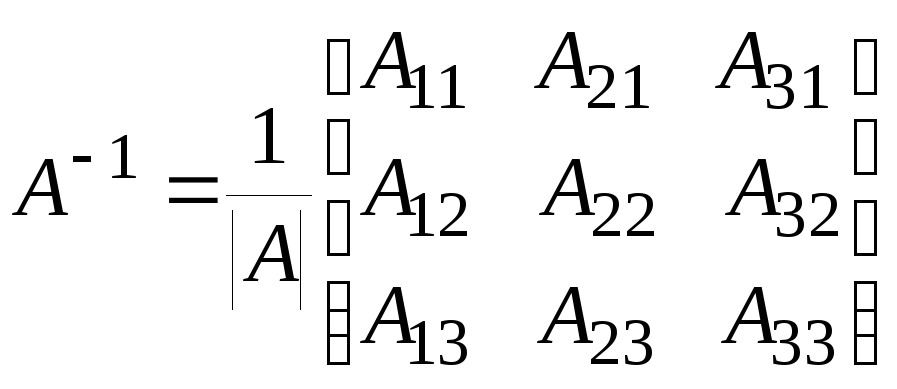
б). С помощью обратной матрицы где- обратная матрица к,- столбец правых частей.

.

; ;;

; ;;

; ;.

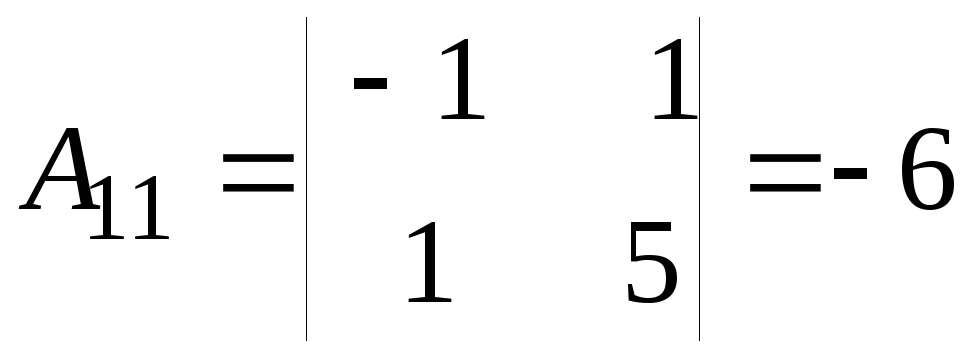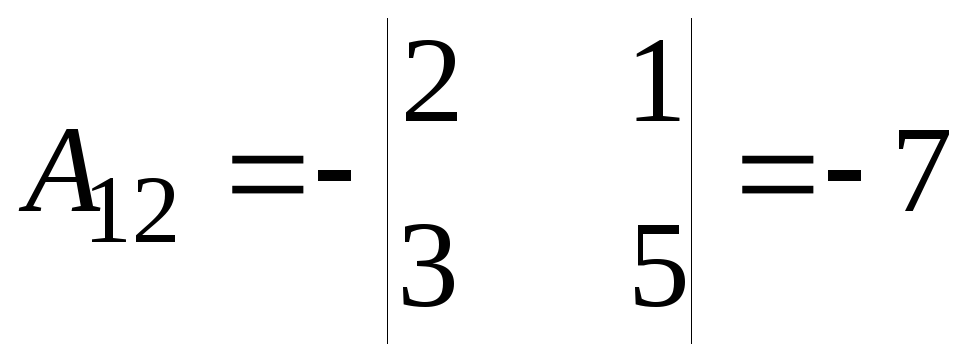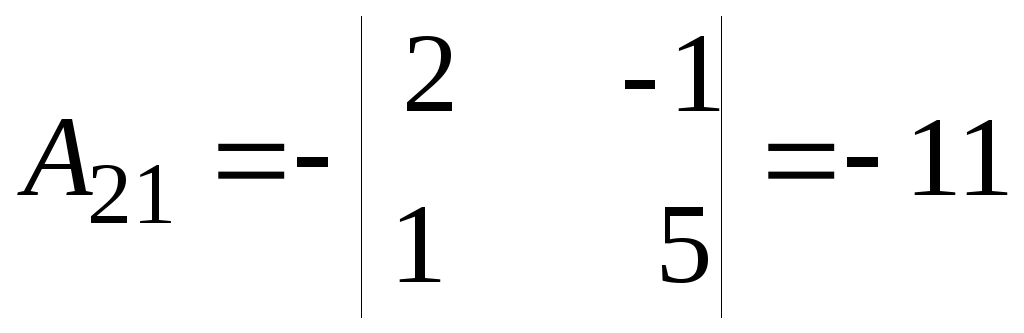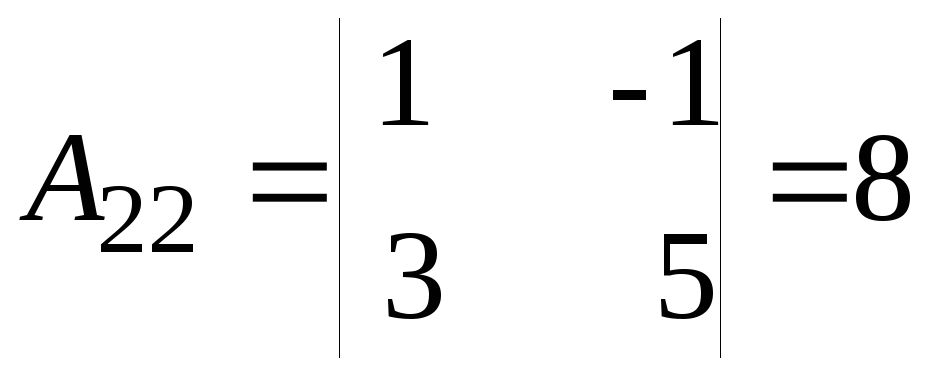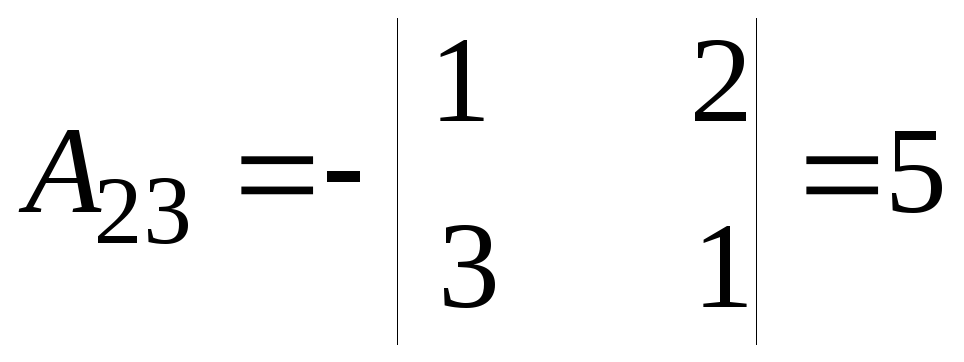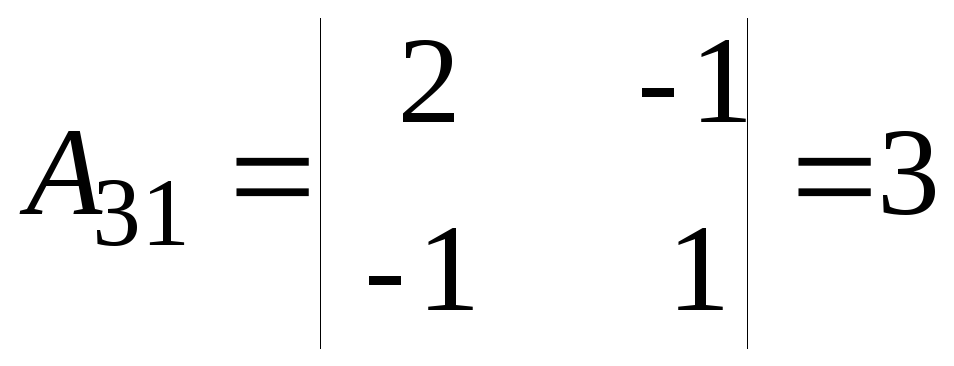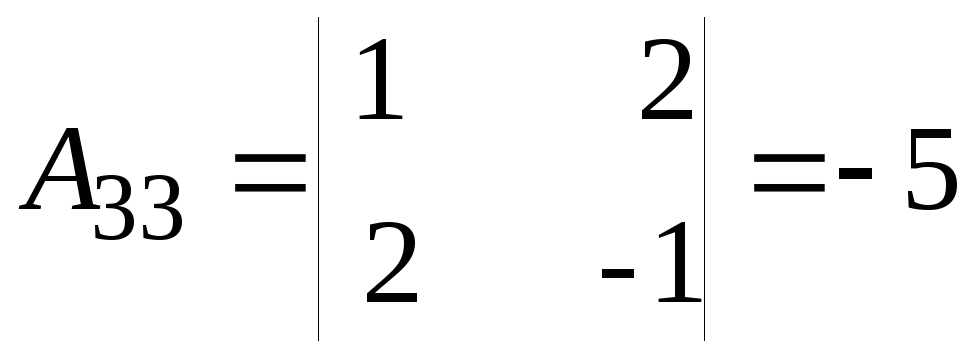Решение системы

,

т.е. .

в). Наша система эквивалентна

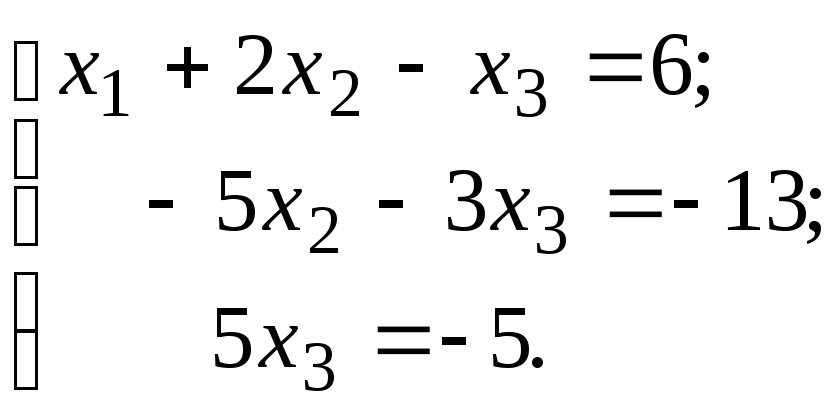
(прямой ход Гаусса совершен при нахождении рангов матриц и).

Тогда

Задача 1.2. Решить однородную систему линейных алгебраических уравнений

С помощью элементарных преобразований матрицу приведем к трапециевидной форме

~ .

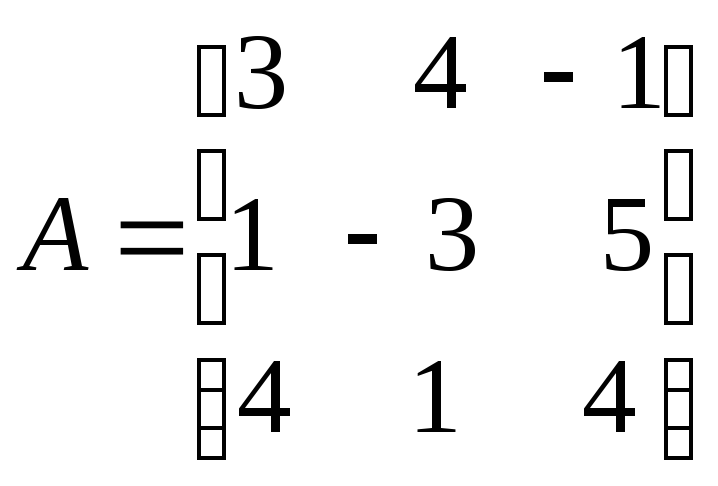Следовательно, 2<3 и система имеет бесконечное множество решений, зависящих от 3-2=1 произвольной постоянной. Исходная система эквивалентна

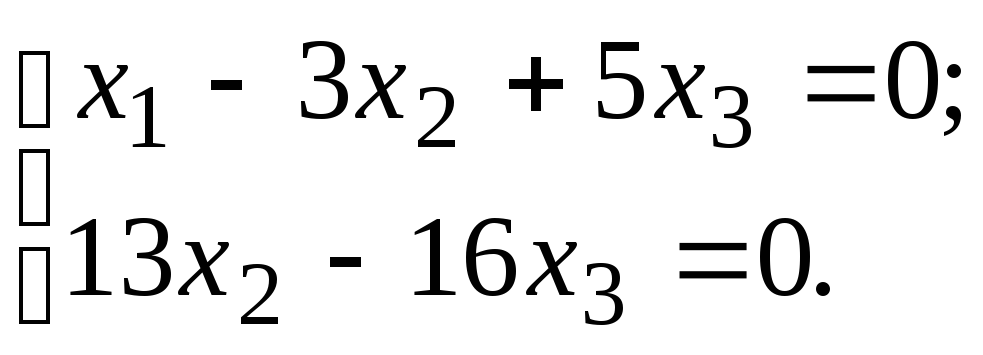
Откуда .

Полагая (произвольной постоянной), имеем

, .

Задача 1.3. По координатам точек ,,найти:

а). Модуль вектора

;

.

б). Скалярное произведение векторов и.

.

в). Проекцию вектора на вектор.

.

г). Координаты точки , делящей отрезокв отношении 1:3;. Следовательно:

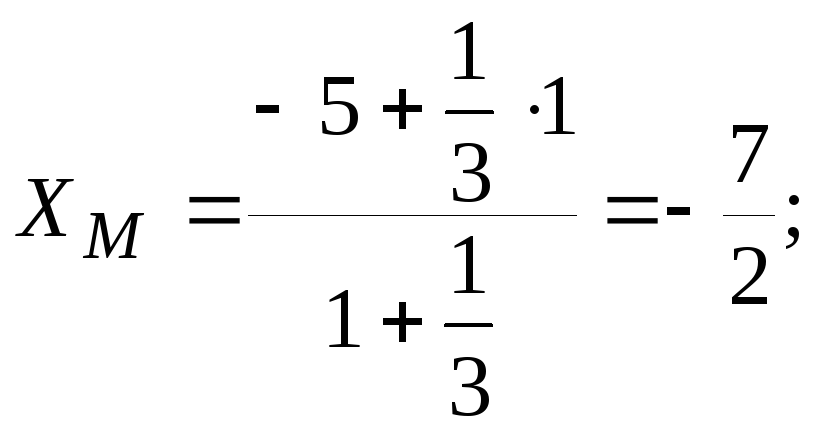
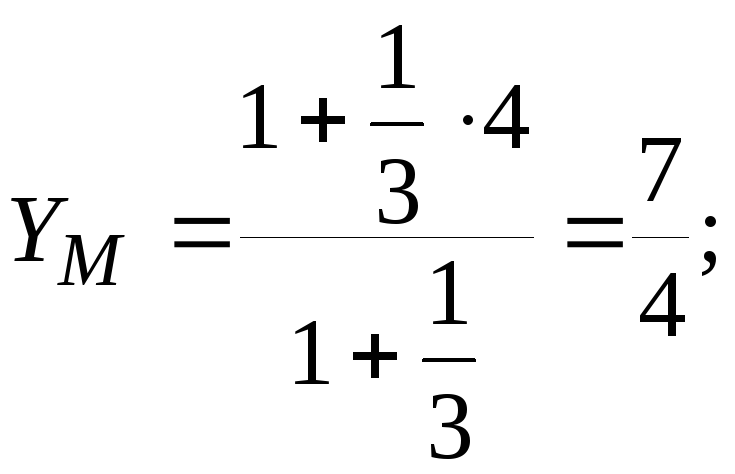
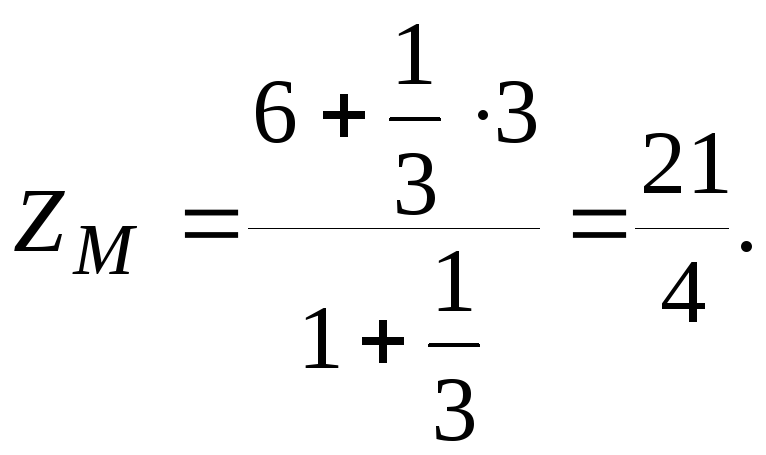
Задача 1.4. Даны векторы Необходимо:

а). Найти модуль векторного произведения .

=;

.

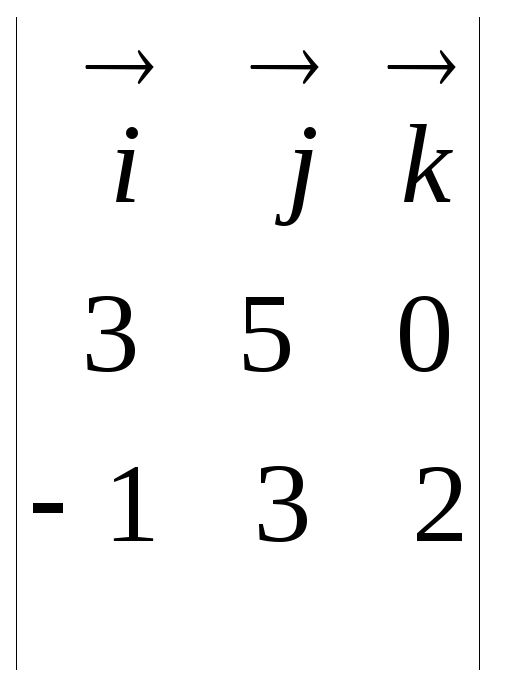
б). Проверить, будут ли коллинеарны или ортогональны два вектора и.

Условие коллинеарности двух векторов

Т.к. то вектораинеколлинеарны.

Условие ортогональности двух векторов

Т.к. то вектора неортогональны.

в). Вычислить смешанное произведение трех векторов

.

.

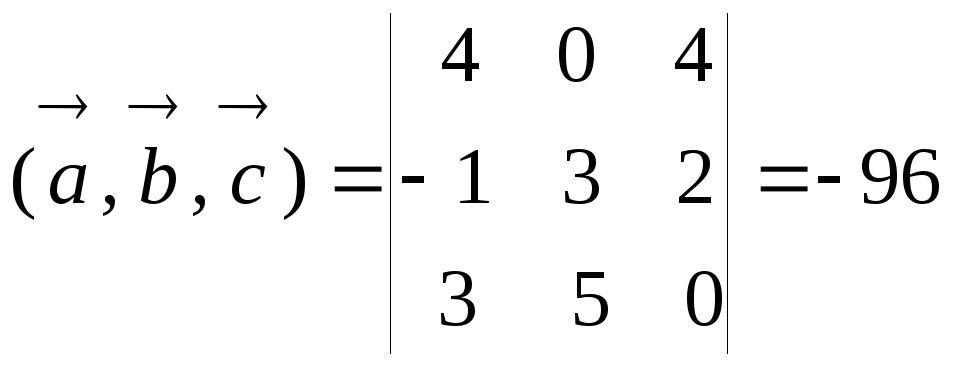г). Проверить, будут ли компланарны три вектора

Вектора компланарны, если

Из пункта в) следовательно, эти векторы некомпланарны.

Задача 1.5. Даны четыре точки

Составить уравнения:

а). Плоскости

Уравнение плоскости по трем точкам имеет вид

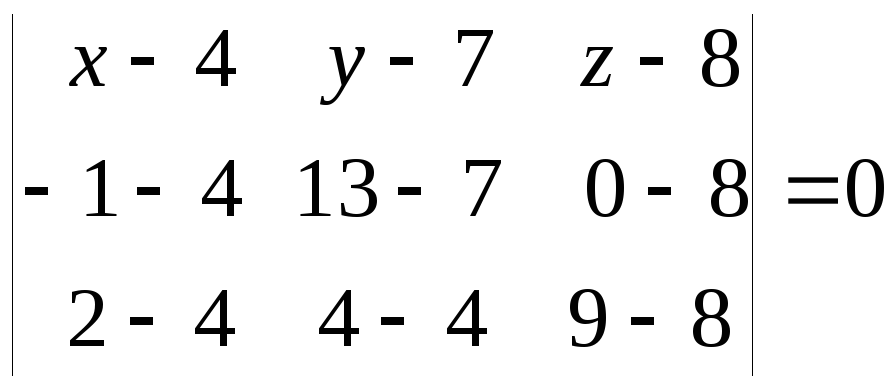, откуда .

б). Прямой

Уравнение прямой по двум точкам

откуда

в). Прямой , перпендикулярной к плоскости.

Из уравнения плоскости следует, что вектор||откуда уравнениеимеет вид

г). Прямой , параллельнойЗначит, вектори уравнение этой прямой имеет вид

д). Плоскости, проходящей через точку перпендикулярно к прямой

Векторперпендикулярен искомой плоскости.

Значит, - ее уравнение, которое приводится к виду

е). Вычислить - угла между прямойи плоскостью.

; ;

.

ж). Косинус угла между координатной плоскостью и плоскостью.

Вектор а вектор. Поэтому

.

Задача 1.6. Составить уравнение плоскости, проходящей через точки ипараллельно прямой, проведенной через точкии

Найти вектор , перпендикулярный искомой плоскости. Векториследовательно, в качестве вектораможно взять

; ;

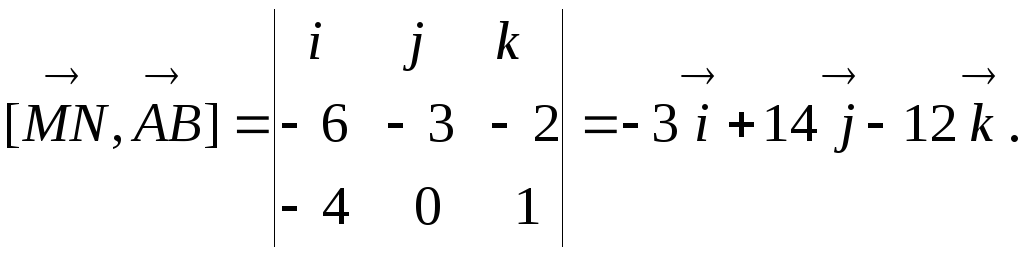
Тогда уравнение искомой плоскости которое приводится к виду

Задача 1.7. Найти уравнение прямой, проходящей через точку пересечения прямых иперпендикулярно первой прямой. Найдем точку:

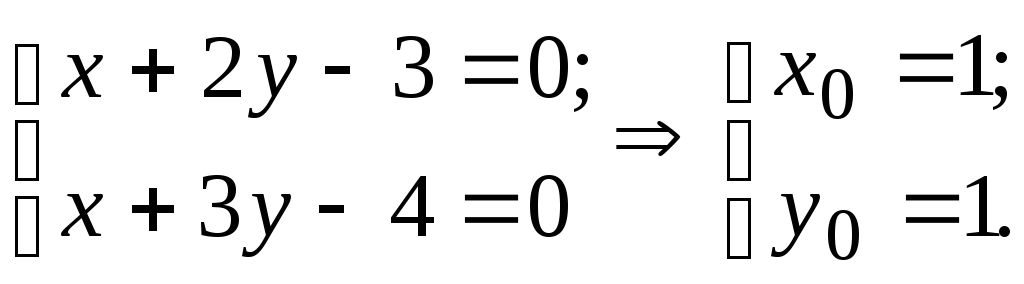
Вектор параллелен искомой прямой. Поэтому ее уравнение запишем каконо приводится к виду

Задача 1.8. Определить вид поверхности и построить ее.

а) . Приведем уравнение к каноническому виду

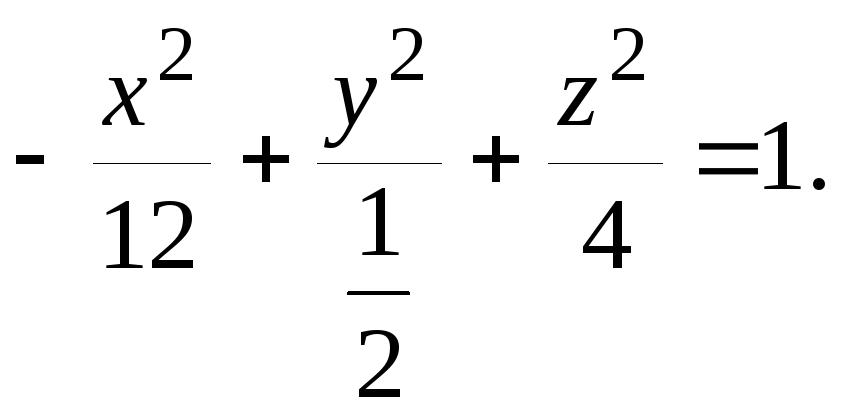
Получим уравнение однополостного гиперболоида, ось которого совпадает с полуоси эллипса в плоскости Y0Z равныиПостроим поверхность.

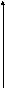Z

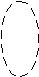
Y

X

б)

Приведем уравнение к каноническому виду .

Это уравнение конуса второго порядка, ось которого совпадает с осью 0Z.

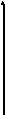Z

Y

X