11.2. Теорема об изменении количества движения точки

Пусть на точку массой m действует система постоянных сил, равнодействующая которых согласно основному закону динамики

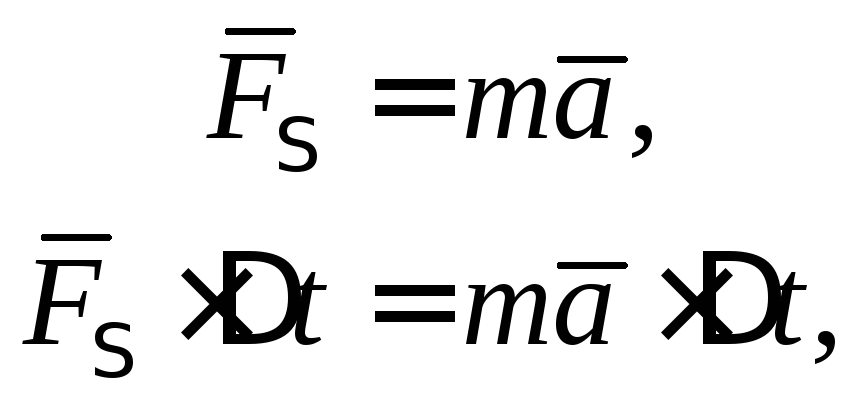
(изменение количества движения точки равно импульсу всех сил).

Спроецировав на оси координат обе части векторного равенства (11.1), в общем случае получим:

а) систему трех скалярных уравне­ний:

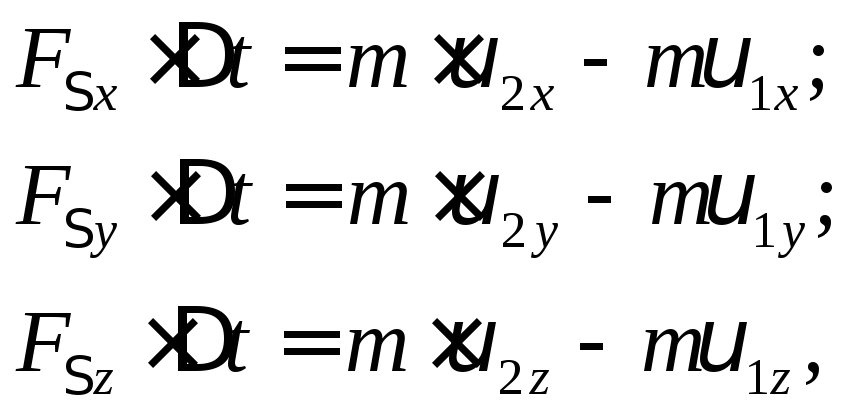
где

б) если силы, действующие на точку, лежат в одной плоскости, то получим два скалярных уравнения;

в) если силы действуют вдоль одной прямой, то, спроецировав уравнение (11.1) на эту прямую, получим одно скалярное уравнение:

.

11.3. Теорема об изменении кинетической энергии точки

Пусть на точку действует система постоянных сил, равнодейст­вующая которых . Допустим, что силы действуют вдоль одной прямой. Тогда

;

.

На прямолинейном пути

Отсюда с учетом того, что ,

,

т. е. изменение кинетической энергии точки равно сумме работ действующих сил.

11.4. Понятие о механической системе

Совокупность материальных точек, связанных между собой сила­ми взаимодействия, называется механической системой (рис. 11.1). Например, механическую систему образуют Земля и Луна или спортивный само­лет и буксируемый им планер.

Любое материальное тело рассматривается в механике как меха­ническая система, образуемая совокупностью материальных точек. Абсолютно твердое тело носит название неизменяемой механической системы, так как расстояние между материальными точками остается неизменным. Изменяемые системы – любые машины или механизмы.

Рис. 11.1. К понятию о механической системе

Если рассматривать какую-либо механическую систему, то силы, действующие на точки системы со стороны точек или тел, не входя­щих в эту систему, называются внешними (F_e, R_e), а силы, дей­ствующие на точки системы со стороны точек или тел этой же сис­темы, называются внутренними (F_i).

Главный вектор всех внутренних сил механической системы равен нулю, причем это условие соблюдается, только если рассматриваемая механическая система неизменя­емая.

Движение механической системы зависит:

1) от действующих сил;

2) суммарной массы системы

,

где m – масса механической системы;

– массы ее отдельных точек;

3) положения центра масс системы.

Движение центра масс определяется (только при поступательном движении) уравнением

,

где – результирующая всех внешних сил, приложенных к точкам системы;

m – масса системы;

– ускорение центра масс системы.

Как видим, это уравнение аналогично основному уравнению динамики точки. Смысл его состоит в том, что центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и приложены все внешние силы.

11.5. Основное уравнение динамики вращающегося тела

Пусть твердое тело (рис. 11.2) под действием внешних сил (эти силы на рис. 11.2 не показаны) вращается около оси OZ с угловым ускорением .

a_kn

ρ_k

a_kt

ΔF_инkn

ΔF_инkt

Рис. 11.2. К определению работы сил, действующих на вращающееся тело

Алгебраическая сумма моментов всех сил (активных сил и сил сопротивления) относительно оси OZ

называется вращающим моментом.

Рассматривая твердое тело как механическую систему, разобьем его на множество материальных точек массами . Каждая из этих точек движется по окружности радиуса , с ускорением , которое разложим на касательное и нормальное ускоре­ние.

Приложим к каждой материальной точке элементарные силы инер­ции: касательную и нормальную . Согласно принципу Даламбера, активные силы, силы реакции связей и силы инерции образуют уравновешенную систему. Поэтому алгебра­ическая сумма моментов всех этих сил относительно оси OZ должна быть равна нулю, т. е.

(моменты сил относительно оси OZ равны нулю, так как линии действия этих сил пересекают ось).

У любой точки вращающегося тела числовое значение касательно­го ускорения ,поэтому значение , где – угловое ускорение тела. Тогда

Величина , равная сумме произведений масс всех точек тела на квадраты их расстояний от оси вращения, называетсямоментом инерции тела (системы) относительно этой оси.

Основное уравнение динамики вращающегося тела:

В СИ момент инерции тела выражается в кг · м².