
- •2. Интегральные суммы и тройной интеграл.
- •3. Правила вычисления двойного интеграла путем сведения к повторному. Пример.
- •4. Приведение двойного интеграла к повторному в случае криволинейной области. Пример.
- •5. Вычисление тройного интеграла по любой области. Пример.
- •6. Геометрический смысл двойного интеграла.
- •7. Основные свойства кратных интегралов.
- •8. Существование кратных интегралов.
- •9. Вычисление двойных двойных интегралов в полярной системе координат. Пример.
- •12. Криволинейный интеграл первого рода. Определение. Сведение к обычному интегралу. Пример.
- •10. Вычисление тройных интегралов в сферических координатах. Пример.
- •11. Вычисление тройных интегралов в цилиндрических координатах. Пример.
- •13. Криволинейный интеграл второго рода. Определение. Сведение к обычному интегралу. Механический смысл. Пример.
- •Сведение криволинейного интеграла второго рода к обычному интегралу.
- •14. Связь между криволинейными интегралами первого и второго рода.
- •15. Поверхностный интеграл первого рода.
- •Сведение поверхностного интеграла первого рода к обычному двойному интегралу.
- •16. Поверхностный интеграл второго рода.
-
Двойной и тройной интеграл
Разбиение плоской фигуры
П усть
Е – плоская фигура, т.е. ЕRn.
Величина sup{(M1,M2)M1E,
M2E}=(по
определению) называется диаметром
(d(E)).
усть
Е – плоская фигура, т.е. ЕRn.
Величина sup{(M1,M2)M1E,
M2E}=(по
определению) называется диаметром
(d(E)).
Фигура Е ограничена, т.е. может быть вписана в многоугольник тогда и только тогда, когда diamE. Ограниченная фигура квадрируема, т.е. имеет площадь (измерима по Жордану) тогда и только тогда, когда ее границы имеют нулевую площадь, т.е. может быть заключена в многоугольник со сколь угодно малой площадью.
Пересечение и объединение конечной совокупности квадрируемых фигур квадрируема. Фигура ограниченная кусочно-гдадким контуром, т.е. конечным числом дуг с непрерывными касательными, квадрируема.
Площадь фигуры Е будем обозначать Е или mesE, или Е.
Определение: Совокупность {Ei}(подмножеств)={E1, E2,…,En} из {E} называется разбиением {E}, если все {Ei} составляют в совокупности фигуру Е (i=1,2,…,n).
Если никакие две разные фигуры {Еi} не имеют общих внутренних точек:
(ЕiEj)=0, ij
тогда:
![]()
Определение: Диаметром разбивки Еi называют величину, равную max(diamEi). Будем обозначать d{Ei}.
1. Интегральные суммы и двойной интеграл.
Пусть на фигуре Е задана ограниченная функция (ЕR2) f. Возьмем разбиение {Ei}, выберем точки xiEi и построим интегральную сумму:
![]()
Определение: Если интегральные суммы при d{Ei}0 имеют предел, т.е. для любого существует такое , что для любого {Ei} и для любого xiEi при d{Ei} выполняется неравенство I-, (т.е. интегральные суммы имеют предел I), то функция называется интегрируемой в смысле Римана на Е, а число I называют двойным интегралом от функции f на Е и обозначают:

2. Интегральные суммы и тройной интеграл.
Пусть ограниченное множество {Ei}R3. В трехмерном случае будем рассматривать области, имеющие в качестве своей границы кусочно-гладкие поверхности, т.е. области, имеющие кусочно-гладкие границы.
Определение: Поверхность называется гладкой, если в любой его точке к ней можно провести касательную плоскость, непрерывно меняющуюся вместе с этой точкой. Поверхность называется кусочно-гладкой, если ее можно разрезать на конечное число гладких кусков.
Для трехмерных ограниченных плоскостей с кусочно-гладкими границами можно определить их объем (их трехмерную меру):
Е, mesE, V.
Зададим на ЕR3 ограниченную функцию f. Зададим разбиение {Ei} и выберем точку хi из {Ei}. Тогда интегральная сумма имеет вид:
![]()
Если интегральная сумма имеет предел I при стремлении d{Ei}0, то это число называется тройным интегралом от функции f на Е и обозначается:
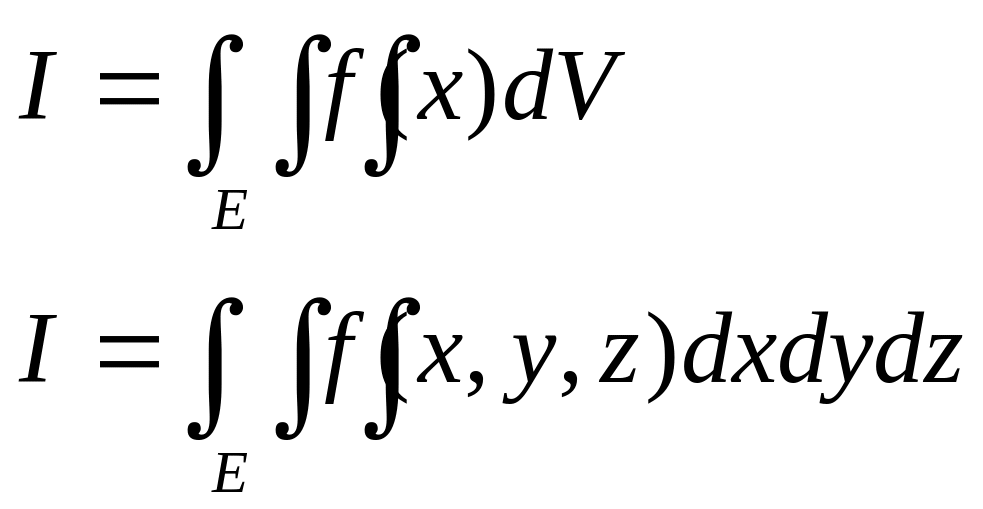
3. Правила вычисления двойного интеграла путем сведения к повторному. Пример.
Пусть на отрезке [а, b] заданы непрерывные функции у0(х) и У(х) такие, что у0(х)≤У(х) для любых х[а, b] и пусть на множестве {Ei} точек (х, у) таких, что a≤x≤b и у0(х)≤у≤ У(х) определена функция f(x, y).
Е сли
для любого фиксированного х[а,
b] функция
f(x,
y) как
функция у интегрируема на отрезке
[у0(х),
У(х)], то это значит, что существует
сли
для любого фиксированного х[а,
b] функция
f(x,
y) как
функция у интегрируема на отрезке
[у0(х),
У(х)], то это значит, что существует
а
функция
интегрируема на отрезке [а, b], то
![]()

называется повторным интегралом и обозначается:
Приведение двойного интеграла к повторному в случае прямоугольной области. Пример.
Теорема:
Если для функции
f(x,
y)
определенной в прямоугольной области
[а,
b][с,
d]
существует
![]()
и
при каждом постоянном значении х[a,b]
существует функция,![]() то
существует также повторный интеграл
то
существует также повторный интеграл
![]()
и выполняется равенство:
![]()
(Е={(x, y)axb, cyd})
Замечание: Меняя ролями х и у можно доказать формулу:
![]()
в
предположении, что для любого фиксированного
у[c,d]
существует
интеграл
![]() .
.
4. Приведение двойного интеграла к повторному в случае криволинейной области. Пример.
Пусть Е криволинейная область существенного типа, т.е. Е – замкнутая область, ограниченная сверху и снизу двумя непрерывными кривыми у=у0(х) и у=У(х) (х[a,b]). С боков область ограничена прямыми х=а и x=b.
Теорема:
Если для функции f(x,y)
определенной на Е существует
![]() и
при любом фиксированном значении х[a,b]
существует простой интеграл
и
при любом фиксированном значении х[a,b]
существует простой интеграл
 ,
то существует и повторный интеграл
,
то существует и повторный интеграл

и выполняется равенство:
![]()
Замечание
1:
Если криволинейная трапеция Е ограничена
кривыми х=х0(у)
и х=Х(у) при у[c,d],
то двойной интеграл
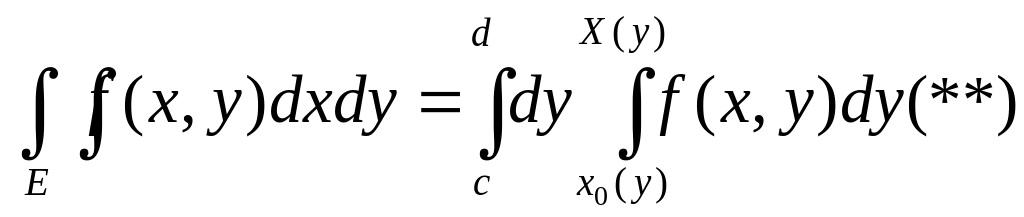
Замечание 2: Если граница области Е пересекается прямыми параллельными осям координат в двух точках, то тогда при выполнении соответствующих условий имеют место обе формулы (*) и (**) и верно равенство (правило замены порядка интегрирования в повторном интеграле):

Замечание 3: В случае более сложной границы область Е распадается на конечное число частей, каждая из которых простейшая (правильная) область.
