11. Вычисление тройных интегралов в цилиндрических координатах. Пример.

Зададим в трехмерном пространстве прямоугольную систему координат x, y, z. Произвольная точка М(x, y, z) пространства определяется также тройкой чисел (, , z), где z – по-прежнему ее аппликата, а (, ) – полярные координаты точки (x, y) плоскости Oxy в предположении, что полярная ось совпадает с положительным направлением оси Ох. Очевидно:

Замечание: Прямая =0, z=z отображается в одну точку (0, 0, z). Этим нарушается взаимная однозначность соответствия.

Координатные поверхности в рассматриваемом случае будут якобианом этого преобразования:

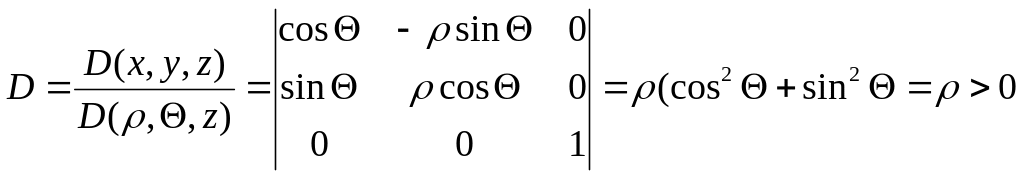Исключая случай =0, якобиан>0.

1. =const – цилиндрические поверхности с образующими параллельными оси z. Направ­ля­ю­щими для них служат окружности на плоскости ху с центром в начале координат;

2. =const – полуплоскости, проходящие через ось z;

3. z=const – плоскости параллельные плоскости ху.

Формула замены переменных в этом случае имеет вид:

Чтобы наглядно получить элемент объема в цилиндрических координатах рассмотрим элементарную область в пространстве (x, y, z), ограниченную двумя цилиндрическими поверхностями радиусов  и +d, двумя горизонтальными плоскостями, лежащими на высотах z и z+dz и двумя полуплоскостями, проходящими через ось z и наклоненными к плоскости xz под углами  и +d. Элемент пространства, ограниченный этими поверхностями, с точностью до бесконечно малых высшего порядка, представляет собой прямоугольный параллелепипед с ребрами d, d, dz. Его объем равен dddz.

13. Криволинейный интеграл второго рода. Определение. Сведение к обычному интегралу. Механический смысл. Пример.

Дадим строгое определение криволинейного интеграла второго рода. Используя предыдущие рассуждения и требуя непрерывности функций Р(х, у) и Q(x, y) вдоль кривой L, составим две интегральные суммы:

Определение: Если существует предел интегральной суммы ₁ (₂) при стремлении к нулю наибольшей из длин l_i, то этот предел называется криволинейным интегралом второго рода и обозначается символом:

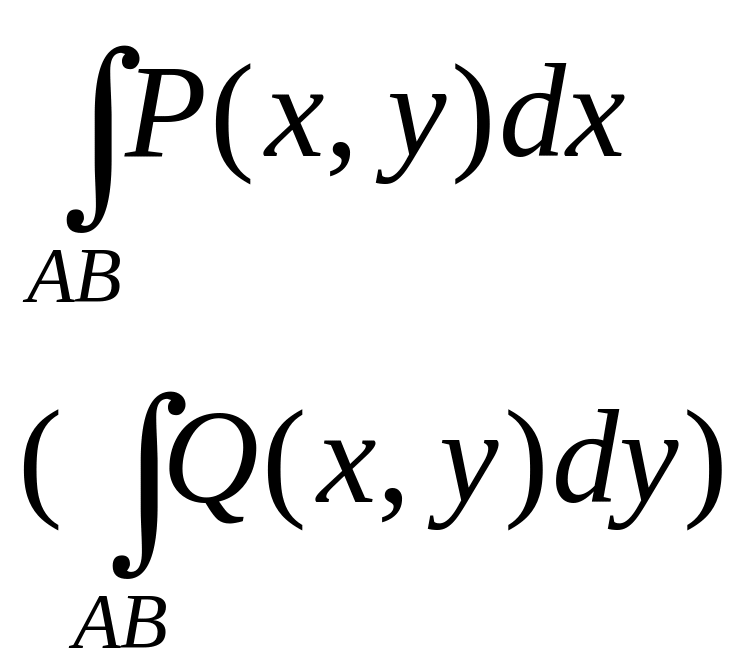
Сумму этих интегралов принято называть общим криволинейным интегралом второго рода и обозначать символом:

Замечание: Из общего вида интегральных сумм (1) и (2) очевидно, что для криволинейного интеграла второго рода изменение направления на кривой ведет к изменению знака, т.е.:

Замечание: Для пространственной кривой аналогично вводятся три криволинейных интеграла второго рода:

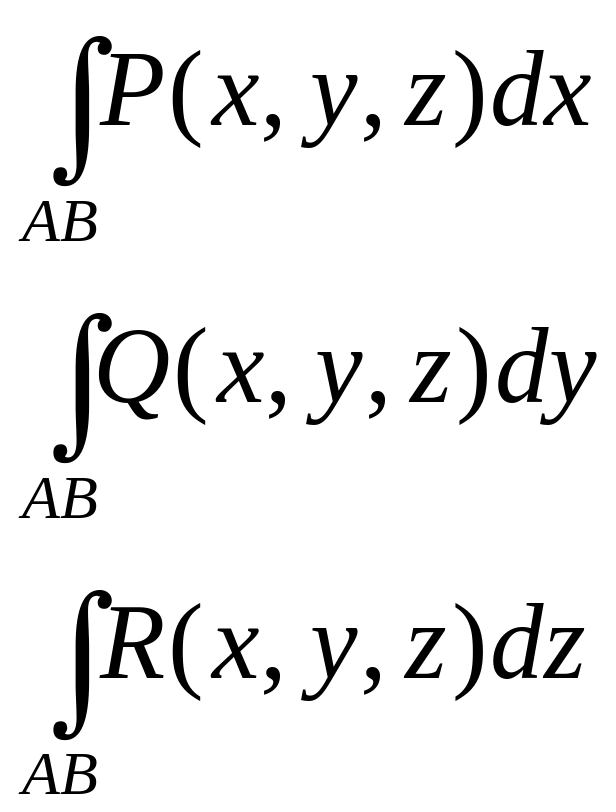
Сумма этих интегралов даст общий криволинейный интеграл второго рода по пространственной кривой:

Сведение криволинейного интеграла второго рода к обычному интегралу.

Теорема: Если кривая L=АВ является гладкой функции P(x, y) и Q(x, y) непрерывны вдоль кривой, то криволинейные интегралы второго рода существуют и имеют место следующие формулы, сводящие криволинейные интегралы к обычным:

Если кривая задана уравнением y=y(x) (x[a, b]) (х – параметр), то:

dy=y(x)dx

14. Связь между криволинейными интегралами первого и второго рода.

Рассмотрим непрерывную гладкую кривую, без точек самопересечения заданную в векторном виде r =r(t), или в координатной форме:

Можно доказать, что для всякой гладкой кривой существует ее представление r =r(l), в котором за параметр l взята переменная длина дуги L. Далее можно доказать, что модуль вектора

Выясним геометрический смысл координат вектора (1). Обозначим углы , , , образованные вектором (1), или что тоже касательной к кривой L={r(t)}, соответственно с осями Px, Oy, Oz. Тогда из равенства (2) следует, что проекции вектора (1) равны соответственно направляющим косинусам:

С другой стороны для вектор-функцииr(l), которая имеет координаты (x(l), y(l), z(l)) имеем:

Отсюда имеем:

Тогда:

Отсюда: