
- •2. Интегральные суммы и тройной интеграл.
- •3. Правила вычисления двойного интеграла путем сведения к повторному. Пример.
- •4. Приведение двойного интеграла к повторному в случае криволинейной области. Пример.
- •5. Вычисление тройного интеграла по любой области. Пример.
- •6. Геометрический смысл двойного интеграла.
- •7. Основные свойства кратных интегралов.
- •8. Существование кратных интегралов.
- •9. Вычисление двойных двойных интегралов в полярной системе координат. Пример.
- •12. Криволинейный интеграл первого рода. Определение. Сведение к обычному интегралу. Пример.
- •10. Вычисление тройных интегралов в сферических координатах. Пример.
- •11. Вычисление тройных интегралов в цилиндрических координатах. Пример.
- •13. Криволинейный интеграл второго рода. Определение. Сведение к обычному интегралу. Механический смысл. Пример.
- •Сведение криволинейного интеграла второго рода к обычному интегралу.
- •14. Связь между криволинейными интегралами первого и второго рода.
- •15. Поверхностный интеграл первого рода.
- •Сведение поверхностного интеграла первого рода к обычному двойному интегралу.
- •16. Поверхностный интеграл второго рода.
12. Криволинейный интеграл первого рода. Определение. Сведение к обычному интегралу. Пример.
Пусть кривая L определена параметрическими уравнениями х=(t) и y=(t) (tх[a, b]). Кривая незамкнутая и без точек самопересечения (L={(x, y) х=(t), y=(t), tх[a, b]})/
Пусть функция f(x,y) определена и непрерывна вдоль кривой L, т.е. ()(0)(x1, y1),(x2, y2)L)[((x1, y1),(x2,y2))f(x1, y1)-f(x2, y2)].
Разобьем [a, b] при помощи точек a=t1<t2<…<tn=b на n частичных отрезков [ti-1, ti] при i=1, 2, … , n, т.е. каждому значению ti на кривой соответствует точка Мi((ti), (ti)), то при указанном разбиении [a, b] вся кривая L=AB распадается на n частичных дуг (М0М1, М1М2,…,Мn-1,Mn).
Выберем на каждой частичной дуге Мn-1,Mn произвольную точку Ni(i, i), координаты которой отвечают некоторому значению i параметра t, т.е. (i=i), i=i). При чем i[ti-1, ti] Пусть Li – длина i-той частичной дуги Мn-1,Mn (i=1, 2, … , n).
Составим интегральную сумму:
![]()
Назовем число I пределом интегральной суммы при стремлении к нулю наибольшей из длин Li, если для любого 0 существует такое 0, что выполняется неравенство - I<, если максимальная из длин дуг i<.
Определение: Если существует предел при стремлении максимальной длины li0, то этот предел называется криволинейным интегралом первого рода от функции f(x, y) по кривой L и обозначается:
![]()
Замечание: Из вида интегральной суммы очевидно, что криволинейный интеграл первого рода не зависит от того, в каком направлении от А к В или от В к А пробегается кривая, т.е. криволинейный интеграл первого рода не зависит от направления движения по пути интегрирования.
Механический смысл криволинейного интеграла первого рода.
Если (х, у) – линейно-непрерывная плотность нити L, то масса нити равна:
![]()
Экономический смысл криволинейного интеграла первого рода.
Если U(x,y) – удельная стоимость провоза груза в точке (х, у) пути L, то стоимость провоза груза по всему пути L равна:
![]()
Теорема о сведении криволинейного интеграла первого рода к обычному интегралу.
Если кривая L является гладкой, а функция f(x, y) непрерывной вдоль этой прямой, то интеграл по кривой f(x, y) существует и справедлива формула:
![]()
Ряд математических и прикладных задач приводят к криволинейным интегралам другого типа, например, если r =r(t) является радиус-вектором движущейся материальной точки, а F =F(t) сила действующая на эту точку, то естественно определить работу силыF вдоль траектории L рассматриваемой точки как интеграл:
![]()
или еслиF(P(x, y), Q(x, y)), dr(dx, dy):
![]()
10. Вычисление тройных интегралов в сферических координатах. Пример.
Рассмотрим сферические координаты. Пусть М некоторая точка пространства. Положение этой точки в пространстве можно определить тремя следующими величинами:
- - длина радиус-вектора точки М;
- - угол, составляемый радиус-вектором с осью Oz – полярной осью;
- - угол, составляемый с осью х проекцией ОМ (вектор)=cos(/2-)=sin радиус-вектора на плоскость ху.
0+, 0, 02, тогда х=sincos, y=sinsin, z=sin(/2-)=cos.
Система уравнений
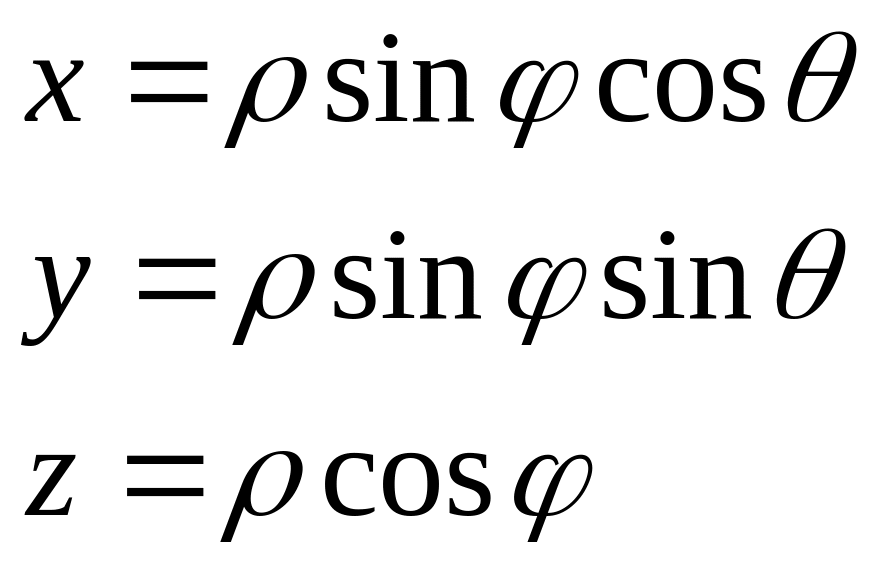
осуществляет переход от полярных координат в пространстве к декартовым координатам.
Замечание: В этом случае мы сталкиваемся с нарушением взаимной однозначности соответствия: Плоскость =0 пространства (, , ) отображается в начале координат z=x=y=0, прямая =0(), = отображается в одну точку x=0, y=0, z=.
Мера множеств, где нарушается взаимооднозначное соответствие, равна 0.! Координатные поверхности сферических координат составляют три семейства:
1. =const – концентрические сферы с центром в начале координат;
2. =const – круговые конусы, осью которых служит ось z;
3. =const – полуплоскости, проходящие через ось z.
Пусть - поверхность, описываемая в полярных координатах функцией =(, ) ((, )).
Функция (, ) непрерывна на замыкании , и пусть - трехмерная область пространства (x, y, z), ограниченная поверхностью и конической поверхностью, лучи которой выходят из нулевой точки и опираются край . Тогда для непрерывной на функции f(x, y, z) имеет место равенство:
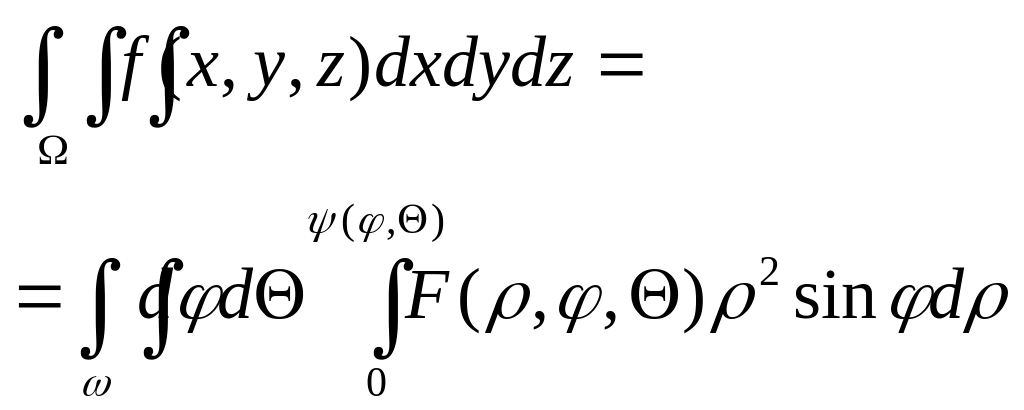
где F(, , )=f(sincos, sinsin, cos),
воспользовавшись формулой замены переменных в тройном интеграле. Т.к. 0, то cos0.
Чтобы наглядно получить элемент объема в полярных координатах, рассмотрим элементарную область (в пространстве (x, y, z)), ограниченную сферами радиусов и +d, конусами, определяемыми углами и +d и полуплоскостями и +d. Эту область можно приближенно принять за прямоугольный параллелепипед с измерениями AD=d, AB=d, AC=OMd= =sind. Т.к. дуга АС равна своей проекции MN, а последняя описана радиусом ОМ=sin и отвечает центральному углу d, то АС=sind. В силу этого объем рассматриваемой области с точностью до бесконечно малых высшего порядка равен:
V=2sinddd
