7.2. Вращательное движение. Угловая скорость, угловое ускорение

Движение твердого тела, при котором все его точки перемещаются по окружности, центры которой расположены на перпендикулярной этим окружностям неподвижной прямой, называется вращательным. Неподвижная прямая, на которой лежат центры круговых траекторий то­чек тела, называется его осью вращения. Для образования оси вра­щения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел можно привести движение две­рей или створок окон при их открывании или закрывании.

Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).

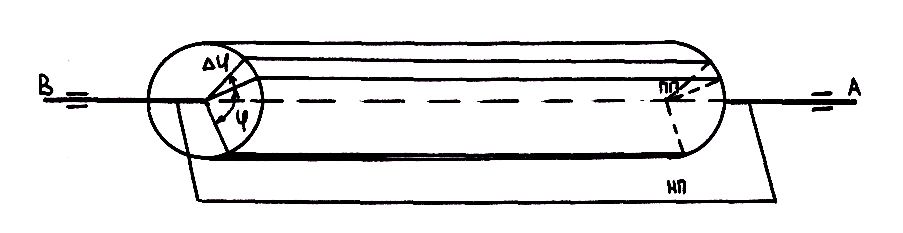
Рис. 7.3. К анализу вращательного движения твердого тела

Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя.

Для установления закона вращательного движения тела, по кото­рому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную полуплоскость НП, а внутри тела отметим подвижную полуплоскость, ко­торая вращается около оси вместе с телом, теперь угол φ, образуемый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, т. е. знать закон вращательного движения тела:

Быстрота изменения угла поворота во времени характеризуется величиной, которая называется угловой скоростью.

Представим, что в некоторый момент времени t положение вращающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело повернулось на угол Δ φ, и величина

называется средней угловой скоростью.

Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение, обозначаемое . Среднее ускорение ;

.

Единица углового ускорения 1 рад/с².

Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часовой стрелки – отрицательным.

б

а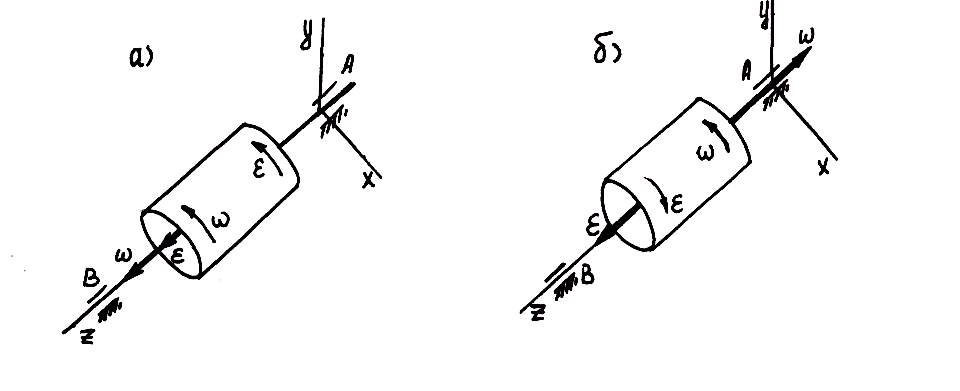

Рис. 7.4. К определению вида вращательного движения

Векторы и – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора (или ), видеть вращение, происходящее против часовой стрелки.

Если векторы и направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы и направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).

7.3. Частные случаи вращательного движения

1. Равномерное вращательное движение. Если угловое ускорение и, следовательно, угловая скорость

, (7.1)

то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных получим

Если при изменении времени от 0 до t угол поворота изменялся от φ₀ (начальный угол поворота) до φ, то, интегрируя уравнение в этих пределах:

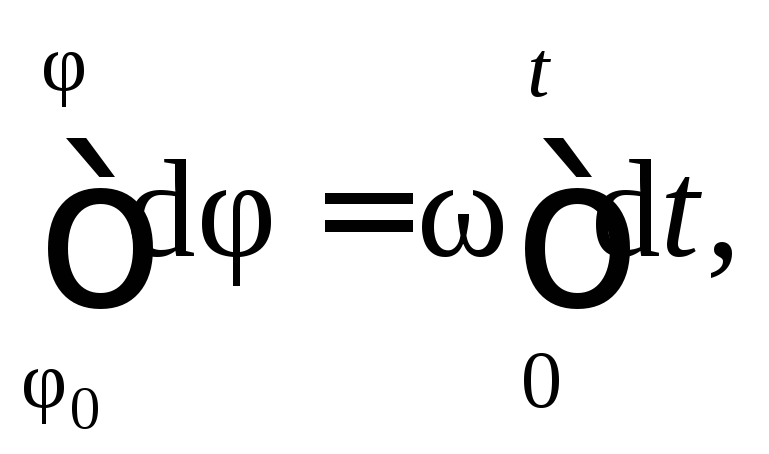
получаем уравнение равномерного вращательного движения

,

которое в окончательном виде записывается так:

.

Если , то

.

Таким образом, при равномерном вращательном движении угловая скорость

или при .

2. Равнопеременное вращательное движение. Если угловое ускорение

(7.2)

то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.2):

и приняв, что при изменении времени от 0 до t угловая скорость изменилась от (начальная угловая скорость) до , проинтегрируем уравнение в этих пределах:

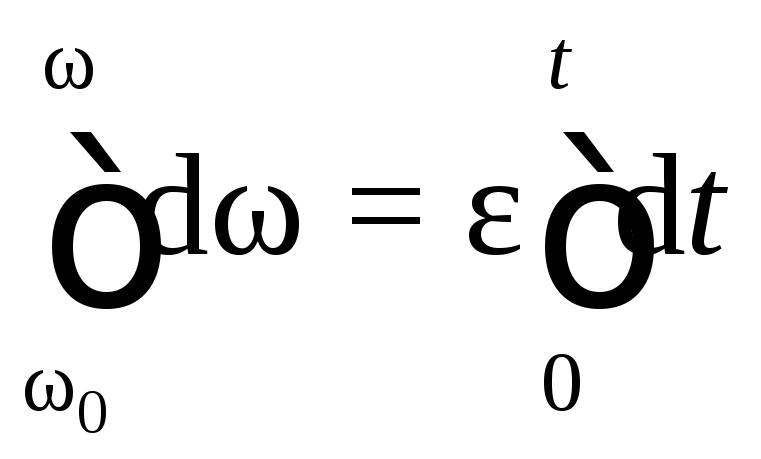или ,

т. е. получим уравнение

(7.3)

выражающее значение угловой скорости в любой момент времени.

Закон равнопеременного вращательного движения или, с учетом уравнения (7.3):

Полагая, что в течение времени от 0 до t угол поворота изменялся от до, проинтегрируем уравнение в этих пределах:

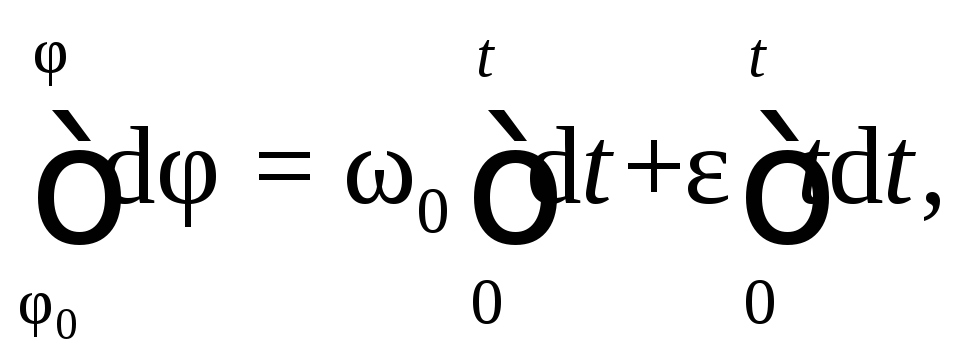или

Уравнение равнопеременного вращательного движения в оконча­тельном виде

(7.4)

Первую вспомогательную формулу получим, исключив из формул (7.3) и (7.4) время:

(7.5)

Исключив из тех же формул угловое ускорение , получим вторую вспомогательную формулу:

(7.6)

где – средняя угловая скорость при равнопере­менном вращательном движении.

Когда и , формулы (7.3)–(7.6) приобретают более простой вид:

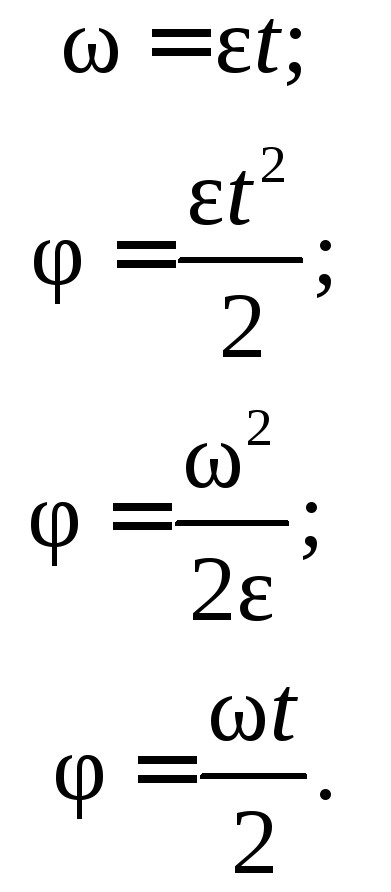
В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.

Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между (с^–1) и n (мин^–1). Так как , то при n (мин^–1) за t = 1 мин = 60 с угол поворота . Следовательно:

.

При переходе от угловой скорости (с^–1) к частоте вращения n (мин^–1) имеем