Тема 6. Метод комплексных амплитуд

КОНТРОЛЬНЫЕ ВОПРОСЫ

1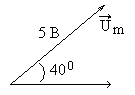. Чему равна комплексная амплитудагармонического напряжения, представленного вектором на рис.6.1? Представьте ее в трех формах записи (показательной, тригонометрической, алгебраической).

Запишите, чему равна комплексная амплитуда в экспоненциальной форме для гармонического напряжения,

Рис. 6.1 представленного равенством

В.

2. Комплексная амплитуда гармонического напряжения в алгебраической форме равна В и частотаГц. Представьте колебание в виде тригонометрической функции времени. Справка: arctg(0,75)= 36,9⁰.

3. По каким формулам осуществляется переход от показательной формы записи комплексного числа к алгебраической и наоборот? Чему равны вещественная и мнимая части комплексного числа в показательной форме? Чему равны модуль и аргумент комплексного числа в алгебраической форме?

4. Чему равна комплексная амплитуда суммы двух гармонических колебаний, заданных своими комплексными амплитудамиии векторами на рис.6.2.? Чему равна амплитудаи начальная фазарезультирующего колебания? Найдите их аналитически, исходя изи. Как их можно найти геометрическим путем, исходя из рис.6.2?

72

5. Чему равны модульи аргументпроизведениядвух комплексных величини?

6. Чему равны модуль и аргументотношения (дроби)двух комплексных чисели?

7. Чему равны модули и

аргументы: Рис. 6.2

а) вещественного числа ;

б) мнимых чисел и;

в) комплексной величины ;

г) числа

?

Справка: arctg(3/5)= 0,54 и arctg(5/3)= 1,03.

8. Изобразите на комплексной плоскости векторы двух гармонических колебаний, заданных комплексными амплитудами:

а) В иА;

б) В иА;

в)В иА;

ЗАДАЧИ

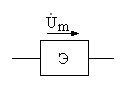
6.1.(1 балл). Гармоническое напряжение на некотором элементе цепи Э (рис.6.3) определяется равенством:

где U_m= ( 800 + (-1)^N10 N ) В, λ = ( 6 G + 0,1 N )⁰.

73

Приведите это выражение к каноническому виду

укажите, чему равна комплексная амплитуда напряжения на элементе Э, представьте ее в алгебраической формеи занесите мнимую часть

Рис. 6.3 в вольтах в АКОС для провер-

ки.

6.2.(2 балла). Комплексная амплитуда напряжения на элементе цепи определяется выражениемгде- вещественная и- мнимая части комплексного числа, задаваемые равенствами :

= (300 + N G ) В ;= (400 + (-1)^N6N ) В.

Найдите при этих значениях ифизическую амплитуду гармонического напряженияна элементе (модуль комплексной амплитуды) и его начальную фазу. Вычислите величину, равную, где- в вольтах,- в радианах, и занесите ее в АКОС для проверки.

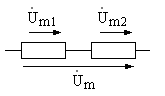
6.3.(3 балла). Напряжения на двух последовательно соединенных элементах цепи (рис.6.4) заданы их комплексными амплитудами в разной форме записи (алгебраической и показательной):

,,

где = 15 ( N + G ) В ;= 25 N В;

= ( 200 + (-1)^N2 N ) В ;

Рис. 6.4 = 0,2 G рад.

74

Найдите комплексную амплитуду суммарного напряжения . Представьте суммарное напряжение в форме тригонометрической функции времени, приняврад/с. Определите мгновенное значение суммарного напряженияв момент временимкс. Занесите значениев вольтах для проверки в АКОС.

6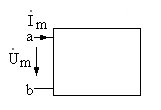.4.(2 балла). Комплексная амплитуда напряжения между выводаминекоторого участка цепи (рис.6.5) в алгебраической форме определяется равенством

где = ( 50 - N ) G В ;

= ( 30 G + 5 N ) В.

Комплексная амплитуда протекающего через цепь тока под действием напряженияв показатель- Рис.6.5

показательной форме равна

где = ( 15 + N ) А,= (-0,3 - (-1)^N+G0,05 N) рад.

Перейдите от комплексных амплитуд напряжения и тока к временным функциям иприрад/с.

Вычислите мгновенную мощность протекающего через тока по формуле в момент времениt= 0,1 G мс. Внесите величинув ваттах для проверки в АКОС.

6.5.(2 балла). При условиях предыдущей задачи представьте напряжение и ток в виде двух векторов на комплексной плоскости. Определите угол (разность фаз) между векторами напряжения и тока

,

где и- начальные фазы напряжения и тока, соответст-

75

венно. Внесите величину в градусах в АКОС для проверки.

6.6.(2 балла). Комплексное сопротивление элемента, участка или целой цепиопределяется отношением комплексных амплитуд напряжения и тока:

.

Определите комплексное сопротивление цепи при следующих данных:

,

где = ( 500 + N G ) В,= N G⁰,

= G А,= (5 + (-1)^N+G0,1 N ) А.

Найдите модуль комплексной величины в омах и внесите его для проверки в АКОС.

ДЛЯ ПЫТЛИВЫХ

6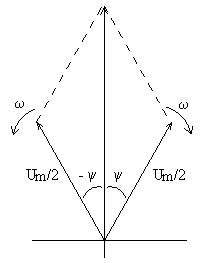.1 Гармоническое колебание представлялось выше в виде вращающегося в положительном направлении (против часовой стрелки) вектора длинойс угловой скоростью.

Применяется другая модель гармонического колебания в виде д в у х векторов длиной , вращающихся в противоположных направлениях с той же угловой скоростью (рис.6.6). Суммарный вектор не вращается с течением времени, а только изменяет свою длину в

Рис. 6.6 положительной или отрицатель-

ной области вертикальной оси.

76

Уравнение процесса (длины суммарного вектора) имеет вид

Покажите, что

,

т.е. что модель действительно представляет гармоническое колебание. Чем отличаются представления гармонического колебания в рассматриваемых моделях?

6.2 Постройте векторную диаграмму, соответствующую комплексному выражению

.

Найдите модуль и аргумент (начальную фазу) колебания, представляемого результирующей комплексной амплитудой .

77