2013.Термодинамика / Paskal / 2011_09_27 / 2011_09_27 / IMG_0028-72-73

— 72-

условлен моделью и не обязан соблюдаться в реальной системе.

Чтобы установить возможность изэнтропического достижения ла­бильного состояния, рассмотрим производную

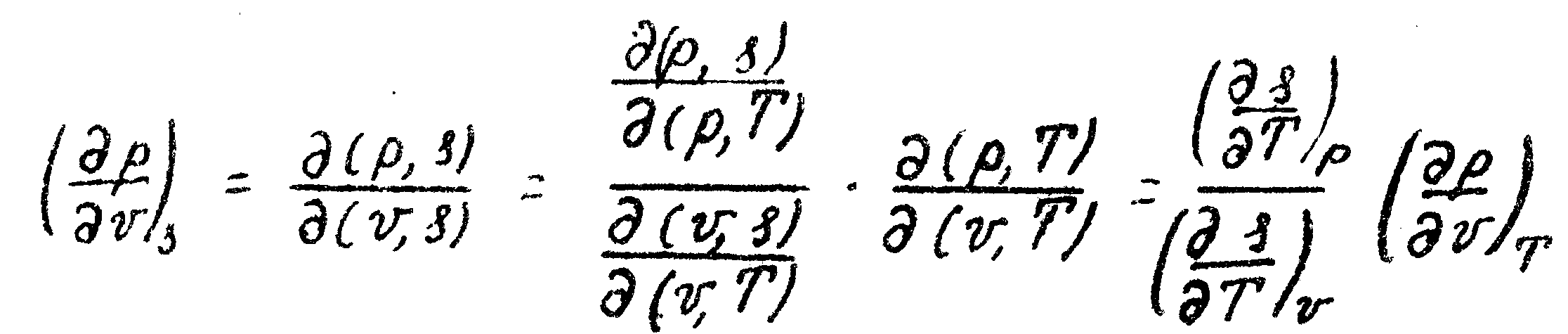
Подставляя сюда (1.6.9) _эполучим

L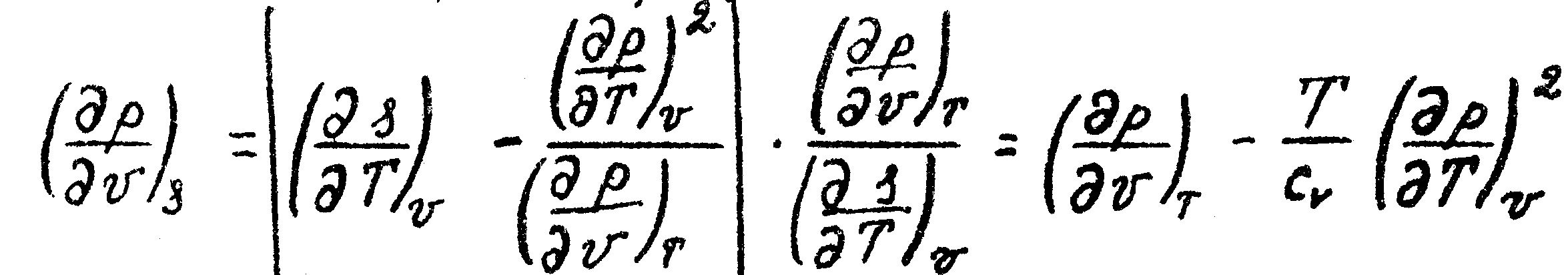

Отсюда видно, что при производная не обращается в нуль, а сохраняет отрицательное значение. Производная обращается в нуль лишь при некотором положительном значении

когда . (1*6 Л?)

Если _, то есть нарушается условие (1.6.10)

то становится больше нуля, то есть система становится не только изотермически, но и изэнтропически (адиабатически) неустойчивой. Как следует из (1.6.9), при этом , то есть система становится и изобарно неустойчивой. Такие состояния недостижимы ни изобарно, ни изотермически, ни изэнтропически (адиабатически).

Условие (16.12) определяет предел изэнтропической (адабатической) устойчивости или изэнтропической (адиабатической) достижимости. Определяя из (1.5.2) значения производных и подставляя их в (1.6.12) получим уравнение предела изэнтропической достижимости в системе Ван-дер-Заальса

-73 -

В последнем выражении слеса стоит функция (§5), справа вместобольшая велйчина Используя график (рис 1-33), мы видим, что линия изэнтропической достижимости на диаграмме состояния образует купол, лежащий внутри спинодали (рис. (1.33) максимума этого купола определится как или

Так, для одно атомной системы и

Рис.1.32 График для определения предела изэнтропической достижимости лабильных состояний;

Рис.1.32 Предел адиабатической достижимости лабильных состояний (штрих пунктирная линия) на диаграмме состояния P-V

Выше отмечалось, что существование лабильного состояния вообще сомнительно. Действительно, строгие статистические расчеты не предсказывают лабильного состояния. Это, впрочем, не обесценивает, проведенный анализ. Следует иметь в виду. Что речь идёт