
attachments_26-06-2014_11-15-16 / Лекц 4 Пар 4 Метод Разд. Пер
.pdf
§4 Метод разделения переменных
Рассмотренный выше метод Даламбера основан на возможности найти общее решение уравнения колебаний. Однако для других уравнений такая возможность представляется очень редко. В этом параграфе излагаются основы метода разделения переменных, который не требует нахождения общего решения исходного уравнения. Начнём с простого примера.
Пример 4.1. Рассмотрим смешанную задачу о свободных колебаниях
струны с закреплёнными концами (в области 0 x l, |
|
t 0). |
|
||||||||||||||||||||||||
|
|
|
|
u |
|
|
a2u |
xx |
0 , |
|
|
|
|
|
|
|
|
|
|
|
(36) |
||||||
|
|
|
|
tt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
u(0, x) sin |
5 x |
, |
u (0, x) sin |
5 x |
, |
|
|
|
|
(36-н) |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
t |
|
|
|
|
|
l |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
u(t,0) 0, |
u(t,l) 0. |
|
|
|
|
|
|
|
|
|
|
(36-г) |
||||||||||||
Обращает на себя внимание сходство правых частей в (36-н). |
|||||||||||||||||||||||||||
Попробуем найти решение в виде u(t, x) F (t) sin |
5 x |
, где функцию F(t) ещё |
|||||||||||||||||||||||||
|
l |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нужно найти. Для этого подставим u(t, x) F (t) sin |
5 x |
в данную задачу. |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
Тогда уравнение (36) примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
F (t) sin |
5 x |
a |
2 |
|
|
25 2 |
F (t) sin |
5 x |
0 , |
|
|
|
(37) |
||||||||||||||
l |
|
|
l |
2 |
|
l |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
из начальных условий (36-н) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
F (0) sin |
5 x |
sin |
|
5 x |
, |
F (0) sin |
5 x |
sin |
5 x |
, |
(37-н) |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
l |
|
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
||||
граничные же условия (36-г) не дадут информации о F(t): F(t) sin 0 0,
F (t) sin 5 0.
Бросается в глаза, что в (37) и (37-н) можно сократить на sin 5 l x . Это и позволяет решить исходную задачу. Сократив, получаем:
F (t) a |
2 |
|
25 2 |
F (t) 0 |
, |
F(0) , |
F (0) . |
(38) |
|
l2 |
|||||||
|
|
|
|
|
|
|
|

То есть, мы получили задачу Коши для обыкновенного дифференциального уравнения на функцию F(t). Его общее решение есть
F (t) C cos |
5a t |
D sin |
5a t |
. Из начальных условий находим значения |
||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
l |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
произвольных постоянных: C , |
|
D |
|
l |
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5a |
|
|
|
|
|
|
|
|
|
|
||
Итак, мы нашли функцию |
F (t) cos |
5a t |
|
l |
|
|
sin |
5a t |
, а значит и |
|||||||||||||||
|
|
5a |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
l |
||||
|
|
|
|
5a t |
|
|
l |
|
|
|
5a t |
|
5 x |
|
|
|
|
|
||||||
u(t, x) cos |
|
|
|
|
|
|
|
sin |
|
|
|
sin |
|
|
. |
|
■ |
|||||||
|
|
|
5a |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
l |
|
|
|
l |
|
|
|
|
l |
|
|
|
|
|
||||||
Обратим внимание, что ключевым обстоятельством, позволившим
исключить переменную x (в составе функции sin |
5 x |
) из исходной задачи |
||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
d 2 |
|
5 x |
2 |
|
|
5 x |
|
||||
(36), (36-н), (36-г), стал тот факт, что |
|
sin |
|
|
25 |
|
sin |
|
|
. |
||||||
dx2 |
|
|
l2 |
|
|
|||||||||||
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
|||
Другими словами, функция sin |
5 x |
|
является собственной для линейного |
|||||||||||||
|
l |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
дифференциального оператора |
|
d 2 |
(относящейся к числу 25 |
2 |
). |
|
||||||||||
|
dx2 |
l2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Возникает, поэтому, естественный вопрос: какие ещё есть собственные
|
d 2 |
функции у оператора |
dx2 , удовлетворяющие условиям (36-г) наподобие |
функции sin 5 l x ? Этот вопрос есть частный случай следующей задачи.
|
|
|
|
u(x) u(x), |
(39) |
|||||||||||||
0 x l, p(x) u (x) q(x) |
||||||||||||||||||
u(0) u (0) 0, |
u(l) u (l) 0 . |
(40) |
||||||||||||||||
Определение 4.2. Задача (39), (40) называется задачей Штурма – |
||||||||||||||||||
Лиувилля, если p(x) 0, |
q(x) 0, |
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
0 . При этом каждое |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значение числового параметра , при котором задача (39), (40) имеет ненулевое решение, называется собственным числом этой задачи.
Замечание. 1) Ш. Штурм (1803–1855), Ж. Лиувилль (1809–1882),
Франция.

2)Упомянутый выше «естественный вопрос» получается из задачи (39),
(40) при p(x) 1, |
q(x) 0, |
1, |
0 . |
|
|||||
Далее в этом параграфе буквой T обозначается оператор Штурма – |
|||||||||
|
d |
|
|
d |
|
|
|
|
|
Лиувилля |
|
p(x) |
|
q(x) , то есть Tu p(x) u q(x) u . Кроме |
|||||
|
|
||||||||
|
dx |
|
dx |
|
|
|
|
||
того, ниже через u0 (x) , ul (x) обозначаются произвольные ненулевые |
|||||||||
решения задач Tu 0, |
u(0) u (0) 0 и |
Tu 0, |
u(l) u (l) 0 |
||||||
соответственно. Такие решения всегда существуют.
Лемма 4.3. Пусть 0 – не собственное число задачи (39), (40). Тогда функции u0 (x) , ul (x) – линейно независимы.
Доказательство. Пусть они линейно зависимы: u0 (x) c ul (x) . Тогда, очевидно, ul (x) – решение задачи Tu 0, u(0) u (0) 0 . Но тогда
ul (x) – ненулевое решение задачи (39), (40) при 0 . Противоречие. ■
Следствие 4.4. Определитель Вронского W (x) |
u0 ul |
(x) 0 . ■ |
|
|
u |
u |
|
|
0 |
l |
|
Лемма 4.5. p(x) W (x) const .
Доказательство – упражнение. Покажите, что p(x) W (x) 0 . Для этого раскройте определитель, умножьте на p(x), возьмите производную, а
затем учтите равенства Tu0 Tul 0 . |
|
■ |
Обозначим символом M(T) множество функций u : 0,l |
, |
|
удовлетворяющих условиям (40) и таких, что Tu L2 0,l . |
|
|
Теорема 4.6. Пусть 0 – не собственное число задачи (39), (40). |
||
Тогда для любой функции f из L2 0,l задача |
|
|
Tu f , |
u M (T ) |
(41) |
имеет единственное решение.
Доказательство. Из леммы 4.3 следует, что общее решение однородного уравнения Tu 0 можно записать в виде
u(x) C u0(x) D ul (x) . Как известно, решение задачи (41) тогда можно искать методом вариации произвольных постоянных в виде
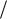
|
u(x) C(x) u0(x) D(x) ul (x) , |
|
|
|
(42) |
||
причём функции C(x), D(x) находят из системы: |
|
|
|
|
|
||
C (x) u0 (x) D (x) ul (x) 0 |
|
|
|
|
|
||
C (x) u |
(x) D (x) u (x) f (x) p (x) . |
|
|
|
(43) |
||
|
0 |
l |
|
|
|
|
|
По следствию 4.4, определитель системы (43) W (x) |
|
u0 ul |
|
( x) 0 . |
|||
|
|
||||||
|
|
|
|
u |
u |
|
|
|
|
|
|
0 |
l |
|
|
Решим её методом Крамера. Аргумент x у функций будем опускать. Лемма 4.5 позволяет вместо pW писать p(0)W(0) или p(l)W(l). Итак,
|
1 |
|
0 |
ul |
|
f ul |
|
|
f ul |
|
|
|
1 |
|
u0 |
0 |
|
f u0 |
f u0 |
|
C |
|
f |
|
|
|
|
|
, |
D |
|
|
f |
|
. |
||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
W |
|
|
|
p W |
|
p(0) W (0) |
W |
|
|
|
p W |
p(0) W (0) |
||||||||
|
p |
ul |
|
|
|
u0 |
p |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Далее, по условию, u(0) u (0) 0 . Учитывая (42), продолжаем: |
|||||||||||||||||||
|
|
|
|
|
|
|
0 C(0) u0 (0) D(0) ul (0) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C (0) u0 |
(0) C(0) u0 |
(0) D (0) ul (0) |
D(0) ul (0) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C(0) u0 (0) u0 |
D(0) ul (0) ul (0) |
|
|
|||||||||||||
C (0) u0 (0) D (0) ul (0)
Впоследнем выражении самая последняя скобка равна нулю в силу первого уравнения системы (43). Коэффициент при C(0) равен нулю по выбору функции u0 (x) . Значит, остаётся равенство
D(0) ul (0) ul (0) 0 , причём выражение в скобке не может быть равно нулю. В самом деле, иначе функция ul (x) – ненулевое решение задачи (39), (40) при 0 . Противоречие. Заключаем, что D(0) 0 .
Аналогично из u(l) u (l) 0 и (42) |
выводим, что C(l) 0 . Значит, |
||||||||||||
|
|
|
l |
|
|
|
1 |
|
|
|
l |
|
|
C(x) C(l) C(x) |
|
C ( y)dy |
|
|
|
|
f ( y) ul ( y)dy , |
|
|||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
p(0) W (0) |
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
1 |
|
|
|
x |
|
|
D(x) D(x) D(0) |
|
D ( y)dy |
|
|
|
|
|
f ( y) u0 ( y)dy . |
|
||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
p(0) W (0) |
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
Подставляя полученные выражения C(x), D(x) в (42), получим |
|
||||||||||||
l |
1 |
|
u0 (x) ul ( y), x y |
|
|
|
|
|
|
||||
u(x) |
|
|
|
|
|
|
|||||||
|
|
u ( y) u (x), x y |
f ( y)dy . |
■ |
|||||||||
p(0) W (0) |
|||||||||||||
0 |
|
|
|
0 |
l |
|
|
|
|
|
|
|
|
