Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

attachments_26-06-2014_11-15-16 / Лекц 7 Пар 5 Основ. Функции

.pdf

Скачиваний:

Добавлен:

30.05.2015

Размер:

409.56 Кб

Скачать

☆

(продолжение)

Лемма 5.8. Если f Lp G , то f f .

Доказательство. Положим q 1 1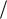 p 1 . Можем записать

(x)

p dx

f ( y) (x y)dy

f ( y)

(x y)dy

f ( y)

(x y) 1 p (x y) 1 q dy

По неравенству Гёльдера последний интеграл не превосходит






	G			n

		1 p
f ( y)	p	(x y) 1 p p dy
f ( y)	p	(x y) 1 p p dy

	1 q p
		dx . (*)
	(x y) 1 q q dy

Так как интеграл от шапочки по

n равен 1, то (*) =

f ( y)

p (x y)dydx

f ( y)

p (x y)dydx

f ( y)

(x y)dxdy

f ( y)

p dy

p .

■

Определение 5.9. Множество всех основных функций, удовлетворяющих определению 5.1 (то есть бесконечно дифференцируемых и финитных), обозначим D G .

Ниже будем обозначать норму функции f из пространства C G через f C , а норму функции f из пространства Lp G – через f L .

Теорема 5.10 (Об аппроксимации основными функциями)

Пусть область G ограничена в

n и содержит носитель измеримой

f f

функции f. Тогда 1) если

f C G

, то

;

2) если f Lp G , то

f f

0 .

f (x) f (x)

Доказательство. 1)

max

f (x) f (x)

. Но

x G

f (x)

(x y)dy

f ( y)

(x y)dy

f (x) f ( y)

(x y)dy

f (x) f ( y)

(x y)dy

max

f (x) f ( y)

(x y)dy

y x

U ( x)

max

f (x) f ( y)

. Поэтому

max

f (x) f ( y)

0 .

y x

x G,

x y

2) Здесь воспользуемся известным фактом, что произвольную функцию f Lp G можно с любой точностью приблизить непрерывной функцией.

Выберем g C G так, чтобы g f L . Тогда

f f L f g L g g L g f L f g L g g L .

Так как g f (g f ) , то по лемме 5.8

g f L (g f ) L g f L . Наконец,

(x) g(x)

p dx max

(x) g(x)

p (G) (G)

x G

в силу п. 1).

■

Доказанную теорему можно переформулировать следующим образом. Следствие 5.11. 1) Множество D(G) всюду плотно в Lp G .

2) D(G) C G всюду плотно в C G .

Выше множество основных функций D(G) рассматривалось как подпространство других (нормированных) пространств. Однако в этом множестве существует своё понятие сходящейся последовательности.

Определение 5.12. Последовательность n n					D G назовём
сходящейся к D G , и напишем n			D(G)
сходящейся к D G , и напишем n			, если:
			n
1)	Существует компакт K, такой, что supp n K G при всех n .
2)	Для любого мультииндекса имеет место равномерная сходимость
	( )	K	( )	.
	n			.
		n

Сейчас мы заведём ещё одно (более широкое) множество основных функций, ослабив в определении 5.1 условие финитности до условия быстрого убывания функций.

Определение 5.13. Будем говорить, что функция : n –
основная из S	n , если она бесконечно дифференцируема и для любого

многочлена P x , любого мультииндекса , любого 0 , найдётся A 0 такое, что P x ( ) x при x A (быстрое убывание).

Множество S

n называется множеством быстро убывающих

функций.

Предложение 5.14. D G S

n .

Утверждение очевидно.

и S n

■

Предложение 5.15. Множества D G

являются векторными

пространствами.

Доказательство. (Упражнение)

■

Пример 5.16.

(Упражнение).

e x2

Пусть x S

n . Для каждого m 0,1, 2,

определим норму

m sup 1

( ) x

: x Rn , k m,

(59)

Из (59) сразу следует

Предложение 5.17. Для каждого x S n

все нормы

существуют и верны неравенства

m .

■

Определение 5.18. Последовательность n

назовём

сходящейся к S n , и напишем n , если

для каждого m 0,1, 2, .

Лемма 5.19. Для каждого x S n

и m 0,1, 2,

выполнено

sup

ix ( ) (x)

(60-84)

x n ;

Доказательство.

( ) x

sup 1

( )

sup sup

1; k,

( ) (x)

sup sup

sup

1; k,

( ) (x)

sup

( ) (x)

sup

x n ; k,

x n ;

■

	Теорема 5.20. Тождественный оператор I ( ) из пространства
D	n в пространство S n является линейным и непрерывным.

Доказательство. Линейность очевидна. Покажем непрерывность. Пусть

m 0 . Тогда на некотором компакте K, содержащем все носители

supp

имеет место равномерная сходимость ( ) 0 . Поэтому

sup

(m ) (x)

sup

(m ) (x)

x Rn ; l k,

x K;l k,

sup

( ) (x) 0 ,

то есть I

0 . ■

x K;

n существует последовательность

Теорема 5.21. Для любого S

такая, что m .

Доказательство. Пусть S n . Выберем m

D n такую,

что m x 1 на шаре Um (0) . Обозначим m x x m x . Тогда

k sup 1

m ( )(x)

sup

m ( )(x)

0 ,

x Rn ,

l k ,

так как m S

■

Таким образом, m .

Соседние файлы в папке attachments_26-06-2014_11-15-16

#
30.05.2015290.22 Кб20Лекц 16 Пар 12 Преобр Фурье ОСН.pdf
#
30.05.2015244.53 Кб24Лекц 3 Пар 3 Метод Даламбера.pdf
#
30.05.2015254.18 Кб21Лекц 4 Пар 4 Метод Разд. Пер.pdf
#
30.05.2015340.54 Кб22Лекц 5 Пар 4 продолжение.pdf
#
30.05.2015425.31 Кб38Лекц 6 Пар 5 Основные функции.pdf
#
30.05.2015409.56 Кб26Лекц 7 Пар 5 Основ. Функции.pdf
#
30.05.2015309 Кб30Лекц 8 Пар 6 Обобщённые функции.pdf
#
30.05.2015302.91 Кб23Лекц 9 Пар 7 Опер с обобщ функ.pdf