ли нейные пространства

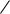
называется плоскостью в Vn. Размерностью плоскости X называется размерность соответствующего подпространства

L dim X dim L .

Одномерная плоскость пространства Vn называется прямой линией.

Плоскость размерности n 1 называется гиперплоскостью. Две плоскости называются совпадающими, если они состо-

ят из одних и тех же точек (векторов) пространства; в противном случае они называются несовпадающими.

Множество точек n-мерного пространства, принадлежащих как плоскости X1, так и плоскости X2, называется их пересечени-

числа, либо как линейное многообразие системой линейных неоднородных уравнений

a11 x1 a12 x2 ... a1n xn a10 a21 x1 a22 x2 ... a2 n xn a20

...

am1 x1 am 2 x2 ... amn xn am 0

ранга n-k, где x1 , x2 , ..., xn — координаты вектора x X .

В частности, всякая прямая задается либо системой линей-

ных уравнений ранга n 1, либо параметрическим уравнением x e a

21

где x1 , x2 , ..., xn — координаты точки x X , x10 , x20 , ..., xn 0 — координаты некоторой фиксированной точки прямой; e1 , e2 , ..., en -

координаты направляющего вектора e прямой.

Всякая гиперплоскость задается одним линейным уравнением a1 x1 a2 x2 ... an xn a0

Приме ры

1. Необходимо найти условия, необходимые и достаточные для того, чтобы две прямые x a0 a1t и x b0 b1t пространства Vn n 1 лежали в одной двумерной плоскости.

Предположим вначале, что две данные прямые лежат в одной плоскости с уравнением

три вектора из двумерного подпространства линейно зависимы. Следовательно, необходимым условием принадлежности пря-

22

уравнение второй прямой можно переписать в виде

x a0 1a1 2b1 tb1

Очевидно, что теперь оба уравнения содержатся в уравнении плоскости H:

x a0 ta1 b1

где t и τ параметры, и, следовательно, прямые принадлежат плоскости H.

2. Найти необходимые и достаточные условия для того, чтобы две прямые x a0 a1t и b0 b1t x проходили через одну

точку, но не совпадали.

Предположим, что при некоторых значениях параметров t t1 для первой прямой и t t2 для второй прямые пересекают-

ся. Тогда

a0 a1t1 b0 b1t2

Отсюда следует, что векторы a0 b0 , a1 , b1 линейно зависимы. Данное соотношение далее можно при известных a0 , b0 , a1 , b1 рассматривать как систему линейных уравнений (в

координатной форме) на определение t1 и t2. Так как прямые не совпадают, то решение системы

единственно. Значит ранг матрицы системы равен 2 и векторы a1 , b1 должны быть линейно независимы. Обратно пусть a1 , b1 –

линейно независимы, векторы a0 b0 , a1 , b1 – линейно зависимы.

Тогда система (4.1) имеет и причем единственное решение. Следовательно, прямые пересекаются в единственной точке.

4.3.Задачи

1.Найти точку пересечения двух прямых a0 a1t и b0 b1t .

23

в n-мерном пространстве и указать необходимые и достаточные условия для каждого из этих случаев.

4.Доказать, что всякая система K 1 точки пространства Vn определяет плоскость размерности r K .

5.Доказать, что линейное многообразие может быть охарактеризовано как множество векторов, содержащее вместе с

любыми двумя векторами x1 и x2 их линейные комбинации

x1 1 x2 при любых α.

6. Найти параметрические уравнения плоскости, заданной общими уравнениями:

7. Найти общие уравнения плоскости, заданной параметрическими уравнениями в координатной форме

5. Евклидовы и унитарные пространства

Определение. Вещественная функция x, y двух векторных аргументов x и y , заданная на линейном пространстве E, называется скалярным произведением, если выполняются сле-

2.x, y x, y x, y E , – вещ. число

3.x y, z x, z y, z

25

4. x, x 0 x 0 , x, x 0 x 0

Определение. Вещественное линейное пространство E, на котором задано скалярное произведение, называется евклидовым пространством.

Прямой подстановкой убеждаемся, что условия 1-4 выполняются. Получим n-мерное евклидово пространство, которое обычно обозначается как En.

В случае комплексного линейного пространства скалярное произведение определяется несколько иным образом.

Определение. Комплексная функция x, y двух векторных аргументов x и y , заданная на комплексном линейном про-

странстве U, называется скалярным произведением, если выполняются следующие условия:

1. x, y y, x * x, y U

2.x, y x, y x, y U , — комплексное число

3.x y, z x, z y, z

4. x, x 0 x 0 , x, x 0 x 0

Комплексное линейное пространство U, на котором задано скалярное произведение, называется унитарным пространст-

вом.

Во всяком унитарном (евклидовом) пространстве имеет ме-

сто неравенство Коши-Шварца:

x, y 2 x, x y, y

сравенством лишь в случае, когда y x .

Введение скалярного произведения позволяет распространить на линейные пространства различные метрические понятия:

26

Введенная функция удовлетворяет следующим условиям

1. x 0 x 0 , x 0 x 0

2. x x

3. x y x y

2. Угол φ между векторами x и y евклидова пространства

определяется как угол, изменяющийся в пределах от нуля до π, косинус которого

cos x, y

x y

3. Расстояние между точками аффинного пространства x и

y, связанного с данным евклидовым, определяется как

x, y x y

5.1.Ортонормированный базис евклидова и унитарного

пространств

Определение. Вектор x называется нормированным, если x 1.

Определение. Два вектора x и y называются ортогональными, если x, y 0 .

Определение. Система векторов e1 , e2 , ..., en евклидова

(унитарного) пространства называется ортогональной, если она либо состоит из одного ненулевого вектора, либо ее векторы попарно ортогональны. Ортогональная система, состоящая из нормированных векторов, называется ортонормированной. Для нее

Всякая ортогональная система линейно независима.

27

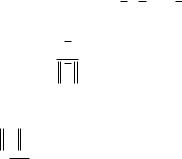
Определение. Базис евклидова (унитарного) пространства, векторы которого e1 , e2 , ..., en образуют ортонормированную сис-

тему, называется ортонормированным базисом.

Заметьте себе, что, в зависимости от того, как введено скалярное произведение, различные системы векторов могут быть или не быть ортонормированными.

Процедура ортогонализации Грама-Шмидта. Для по-

строения ортонормированной системы векторов и, в частности, ортонормированного базиса e1 , e2 , ..., en может быть использова-

на следующая процедура. Пусть векторы f1 , f2 , ..., fn — линейно независимы. Первый вектор ортонормированной системы

e1 f1 f1

Второй вектор

Наконец, векторы ek k 3, n определяются соотношениями

Пример . Необходимо ортогонализировать систему векто-

ров

y y1 ,..., y4 определяется как

4

x, y xi yi

i 1

28

29

Во всяком ортонормированном базисе e1 , e2 , ..., en унитарного (евклидова) пространства скалярное произведение векторов x и y с координатами x1 , x2 , ..., xn и y1 , y2 , ..., yn

n

x, y xi yi

i 1

Координаты вектора x

xi x,ei

5.2. Ортогональное дополнение

Определение. Два множества F и G векторов евклидова пространства E называются ортогональными, если каждый вектор из F ортогонален каждому вектору из G.

Определение. Пусть F – подпространство E. Совокупность всех векторов подпространства E, ортогональных подпространству F, называется ортогональным дополнением F подпространства F.

Всякое ортогональное дополнение F является, в свою очередь, линейным подпространством.

Всякое произвольное евклидово пространство E разлагается в прямую сумму своего произвольного подпространства F и его ортогонального дополнения F

E F F

При ме ры

1. Требуется найти базис ортогонального дополнения L подпространства L, натянутого на векторы