Госы 5к Надя / лекции_3 / kr-int

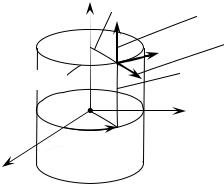
рЛ˜ВТНУИ ТЛТЪВП˚ НУУр‰ЛМ‡Ъ Л НУУр‰ЛМ‡ЪМ˚В ОЛМЛЛ ρ , ϕ , Ë z ËÁÓ·ð‡ÊÂÌ˚ ̇ ðËÒ. 1.4.8.

y

0

ϕ

x

êËÒ. 1.4.8

зВФУТрВ‰ТЪ‚ВММУ ЛБ рЛТ. 1.4.6 ПУКМУ ЫТЪ‡МУ‚ЛЪ¸ Т‚flБ¸ ПВК‰Ы ‰ВН‡рЪУ‚˚ПЛ Л ˆЛОЛМ‰рЛ˜ВТНЛПЛ НУУр‰ЛМ‡Ъ‡ПЛ:

x = ρcosϕ y = ρsinϕ .

z =z

ç‡È‰ÂÏ flÍÓ·Ë‡Ì ÔðÂÓ·ð‡ÁÓ‚‡ÌËfl ‰Îfl ˆËÎË̉ð˘ÂÒÍËı ÍÓÓð‰Ë- ̇Ú:

Hρ =1, Hϕ =1, Hz =1.

C Ы˜ВЪУП ˝ЪЛı ТУУЪМУ¯ВМЛИ ФУОЫ˜ЛП:

41

З˚˜ЛТОflfl ТН‡ОflрМ˚В ФрУЛБ‚В‰ВМЛfl УрЪУ‚ ρ0 , ϕ0 Ë z0 , МВЪрЫ‰МУ Ы·В‰ЛЪ¸Тfl, ˜ЪУ ρ0 ϕ0 = ρ0 z0 = ϕ0 z0 = 0 , Ъ.В. ПУКМУ Т‰ВО‡Ъ¸ ‚˚‚У‰, ˜ЪУ ˆЛОЛМ‰рЛ˜ВТН‡fl ТЛТЪВП‡ НУУр‰ЛМ‡Ъ УрЪУ„УМ‡О¸М‡.

ЦТОЛ ФУОУКЛЪ¸ z = 0, ÚÓ Ï˚ ÔðˉÂÏ Í ËÁ‚ÂÒÚÌ˚Ï ÛÊ ÔÓÎflðÌ˚Ï ÍÓÓð‰ËÌ‡Ú‡Ï ρ , ϕ :

x= ρcosϕ

y= ρsinϕ .

зВЪрЫ‰МУ Ы·В‰ЛЪ¸Тfl, ˜ЪУ ‰Оfl ФУОflрМ˚ı Л ˆЛОЛМ‰рЛ˜ВТНЛı НУУр- ‰ЛМ‡Ъ ‚˚р‡КВМЛfl ‰Оfl flНУ·Л‡М‡ ФрВУ·р‡БУ‚‡МЛfl ТУ‚Ф‡‰‡˛Ъ, Ъ.В.

J(ρ,ϕ,z) =J(ρ,ϕ) = ρ .

7. б‡ПВ˜‡МЛВ (У „ВУПВЪрЛ˜ВТНУП ТП˚ТОВ flНУ·Л‡М‡).

к‡ТТПУЪрЛП УрЪУ„УМ‡О¸МЫ˛ НрЛ‚УОЛМВИМЫ˛ ТЛТЪВПЫ НУУр‰ЛМ‡Ъ Oξη , Ë ÔÛÒÚ¸ ‰Â͇ðÚÓ‚˚ ÍÓÓð‰Ë̇Ú˚ x Ë y Т‚flБ‡М˚ Т НрЛ‚УОЛМВИМ˚ПЛ ξ Ë η ТУУЪМУ¯ВМЛflПЛ:

x =x(ξ,η) , y =y(ξ,η) ,

Ôð˘ÂÏ Ôð‰ÔÓ·„‡ÂÚÒfl, ˜ÚÓ flÍÓ·Ë‡Ì ÔðÂÓ·ð‡ÁÓ‚‡ÌËfl

J(ξ,η) =xξ′ yη′ −xη′ yξ′ ≠ 0 .

0 x 01 ξ

êËÒ. 1.4.9

ÖÒÎË ÙÛÌ͈ËË x(ξ,η) Ë y(ξ,η) МВФрВр˚‚М˚ Л ЛПВ˛Ъ МВФрВр˚‚- М˚В ˜‡ТЪМ˚В ФрУЛБ‚У‰М˚В ФВр‚У„У ФУрfl‰Н‡, ‡ Ъ‡НКВ МВФрВр˚‚М˚В ТПВ¯‡ММ˚В ФрУЛБ‚У‰М˚В, ЪУ ‚ ˝ЪУП ТОЫ˜‡В ПУКМУ ‰УН‡Б‡Ъ¸, ˜ЪУ ФОУ˘‡‰Л SD Ë S Т‚flБ‡М˚ ТУУЪМУ¯ВМЛВП

42

SD = J(ξ,η) S ,

„‰Â (ξ,η) – МВНУЪУр‡fl «ТрВ‰Мflfl» ЪУ˜Н‡ У·О‡ТЪЛ . аБ ˝ЪУ„У ТУУЪМУ¯ВМЛfl ‚˚ЪВН‡ВЪ У˜В‚Л‰М˚И „ВУПВЪрЛ˜ВТНЛИ ТП˚ТО flНУ·Л‡М‡ ФрВУ·р‡БУ‚‡МЛfl. Д ЛПВММУ: П˚ ПУКВП ТН‡Б‡Ъ¸, ˜ЪУ ПУ‰ЫО¸ flНУ·Л‡- М‡ ФрВУ·р‡БУ‚‡МЛfl J(ξ,η) ФрЛ ФВрВıУ‰В Н НрЛ‚УОЛМВИМ˚П НУУр-

‰ËÌ‡Ú‡Ï ‰‡ÂÚ Ì‡Ï ÍÓ˝ÙÙˈËÂÌÚ ËÒ͇ÊÂÌËfl ÔÎÓ˘‡‰ÂÈ ÓÚÓ·ð‡Ê‡Â- Ï˚ı ӷ·ÒÚÂÈ.

еУКМУ ‰УН‡Б‡Ъ¸ Ъ‡НКВ, ˜ЪУ ‰Оfl ФрУТЪр‡МТЪ‚ВММУ„У ТОЫ˜‡fl, НУ- „‰‡ УТЫ˘ВТЪ‚ОflВЪТfl ФВрВıУ‰ УЪ ‰ВН‡рЪУ‚˚ı НУУр‰ЛМ‡Ъ x , y Ë z Н НрЛ‚УОЛМВИМ˚П ξ , η, ζ ФрЛ ‚˚ФУОМВМЛЛ ТУУЪ‚ВЪТЪ‚Ы˛˘Лı ФрВ‰- ФУОУКВМЛИ (МВФрВр˚‚МУТЪ¸ ЩЫМНˆЛИ, Лı ˜‡ТЪМ˚ı ФрУЛБ‚У‰М˚ı Л Ъ.Ф.) ЛПВВЪ ПВТЪУ ТУУЪМУ¯ВМЛВ vT = J(ξ,η,ζ ) vT′, „‰Â vT – Ó·˙ÂÏ

ÏÓ‚.

8. б‡ПВМ‡ ФВрВПВММ˚ı ‰‚УИМ˚ı ‚ ЪрУИМ˚ı ЛМЪВ„р‡О‡ı.

èÛÒÚ¸ ÓÒÛ˘ÂÒÚ‚ÎflÂÚÒfl ÔÂðÂıÓ‰ ÓÚ ‰Â͇ðÚÓ‚˚ı ÍÓÓð‰ËÌ‡Ú x Ë y Н НрЛ‚УОЛМВИМ˚ПЛ ξ Ë η:

x=x(ξ,η)

y=y(ξ,η) .

ирВ‰ФУОУКЛП, ˜ЪУ ‚˚ФУОМВМ˚ ЫТОУ‚Лfl ФрВ‰˚‰Ы˘В„У Ф‡р‡„р‡Щ‡ УЪМУТЛЪВО¸МУ ЩЫМНˆЛИ x(ξ,η) , y(ξ,η) , ξ =ξ(x,y) Ë η =η(x,y) Л Лı ˜‡ТЪМ˚ı ФрУЛБ‚У‰М˚ı Л ЛПВВЪ ТЛОЫ ‚ТВ ТН‡Б‡ММУВ У· У·О‡ТЪflı D Ë

. иЫТЪ¸, НрУПВ ЪУ„У, ‚ У·О‡ТЪЛ D Б‡‰‡М‡ МВФрВр˚‚М‡fl ЩЫМНˆЛfl f(x,y) .

к‡ТТПУЪрЛП ‰‚УИМУИ ЛМЪВ„р‡О I = ∫∫f(x,y)dxdy.

D

лУТЪ‡‚ЛП ЛМЪВ„р‡О¸МЫ˛ ТЫППЫ ‰Оfl ˝ЪУ„У ‰‚УИМУ„У ЛМЪВ„р‡О‡:

n

σn = ∑f(xk ,yk ) SDk . k=1

43

аБПВО¸˜‡fl ‰рУ·ОВМЛВ Л ЫТЪрВПОflfl р‡М„ ‰рУ·ОВМЛfl Н МЫО˛, ФУОЫ˜ЛП:

limσn = ∫∫f (x(ξ,η),y(ξ,η)) J(ξ,η) dξdη .

n→∞

λ→0

ирЛПВр 1. З˚˜ЛТОЛЪ¸:

I = ∫∫(x2 +xy)dxdy ,

D

„‰Â D ÂÒÚ¸ ÍðÛ„ x2 +y2 ≤R2 (ðËÒ. 1.4.10). ê¯ÂÌËÂ. иВрВИ‰ВП Н ФУОflрМ˚П НУУр‰ЛМ‡Ъ‡П.

x=rcosϕ

y=rsinϕ

y

к.л. ϕ R

к.л. r

D

−R

êËÒ. 1.4.10

з‡И‰ВП Ыр‡‚МВМЛВ УНрЫКМУТЪЛ x2 +y2 =R2 ‚ ÔÓÎflðÌ˚ı ÍÓÓð‰Ë-

М‡Ъ‡ı. аПВВП:

(rcosϕ)2 +(rsinϕ)2 =R2 r2 (cos2 ϕ +sin2 ϕ) =R2 r =R

44

íÓ„‰‡

I = R4 2∫π (cos2 ϕ +cosϕ sinϕ)dϕ =

4 0

б‡ПВЪЛП, ˜ЪУ ‰Оfl ЪУ„У, ˜ЪУ·˚ р‡ТТЪ‡‚ОflЪ¸ ФрВ‰ВО˚ ЛМЪВ„рЛрУ‚‡- МЛfl, ‰УТЪ‡ЪУ˜МУ ‚˚flТМЛЪ¸, Н‡Н ФрУıУ‰flЪ (‚УБр‡ТЪ‡˛Ъ) ˜ВрВБ У·О‡ТЪ¸ D НУУр‰ЛМ‡ЪМ˚В ОЛМЛЛ r Ë ϕ .

ирВ‰ФУОУКЛП ‰‡ОВВ, ˜ЪУ МЫКМУ ‚˚˜ЛТОЛЪ¸ ЪрУИМУИ ЛМЪВ„р‡О

I = ∫∫∫f(x,y,z) dxdydz ,

T

ËФЫТЪ¸ УТЫ˘ВТЪ‚ОflВЪТfl ФВрВıУ‰ Н НрЛ‚УОЛМВИМ˚П НУУр‰ЛМ‡Ъ‡П ξ ,

η, ζ ФУ ЩУрПЫО‡П:

x=x(ξ,η,ζ )

y=y(ξ,η,ζ ) .

z=z(ξ,η,ζ )

ирВ‰ФУОУКЛП, ˜ЪУ УЪМУТЛЪВО¸МУ ЩЫМНˆЛИ x(ξ,η,ζ ), y =y(ξ,η,ζ ) , z =z(ξ,η,ζ ) , ξ =ξ(x,y,z), η =η(x,y,z) , ζ =ζ (x,y,z) Ë

Лı ˜‡ТЪМ˚ı ФрУЛБ‚У‰М˚ı ЛПВВЪ ПВТЪУ, ТН‡Б‡ММУВ ‚ Б‡ПВ˜‡МЛЛ Ф. 7.

45

СУФЫТЪЛП Ъ‡НКВ, ˜ЪУ ‚ У·О‡ТЪЛ T ÙÛÌ͈Ëfl f(x,y,z) МВФрВр˚‚М‡. нУ„‰‡, ‡М‡ОУ„Л˜МУ ‚˚¯ВТН‡Б‡ММУПЫ УЪМУТЛЪВО¸МУ ‰‚УИМУ„У ЛМЪВ-

„р‡О‡, ЛПВВЪ ПВТЪЛ ТУУЪМУ¯ВМЛВ:

∫∫∫f(x,y,z) dxdydz =

= ∫∫∫f [x(ξ,η,ζ ),y(ξ,η,ζ ),z(ξ,η,ζ )] J(ξ,η,ζ ) dξdηdζ

T

„‰Â J(ξ,η,ζ ) – flÍÓ·Ë‡Ì ÔðÂÓ·ð‡ÁÓ‚‡ÌËfl.

СОfl р‡ТТЪ‡МУ‚НЛ ФрВ‰ВОУ‚ ЛМЪВ„рЛрУ‚‡МЛfl ФУ ФВрВПВММ˚П ξ , η, ζ ТОВ‰ЫВЪ ‚˚flТМЛЪ¸, Н‡Н ФрУıУ‰flЪ НУУр‰ЛМ‡ЪМ˚В ОЛМЛЛ ξ , η, ζ

z

êËÒ. 1.4.11

ê¯ÂÌËÂ. З˚˜ЛТОЛП ‚УТ¸ПЫ˛ ˜‡ТЪ¸ ФОУ˘‡‰Л ФУ‚ВрıМУТЪЛ ТЩВ- р˚, ОВК‡˘Ы˛ ‚ ФВр‚УП УНЪ‡МВ:

46

аЪ‡Н, ЛПВВП:

З˚˜ЛТОЛП

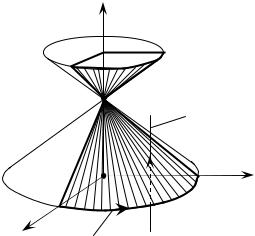
ирЛПВр 3. з‡ИЪЛ У·˙ВП ЪВО‡, ОВК‡˘В„У ‚ ФВр‚УП УНЪ‡МВ Л У„- р‡МЛ˜ВММУ„У ТМЛБЫ НУМЛ˜ВТНУИ ФУ‚ВрıМУТЪ¸˛ x2 +y2 =z2 , Ò‚ÂðıÛ ¯‡ðÓ‚ÓÈ ÔÓ‚ÂðıÌÓÒÚ¸˛ x2 +y2 +z2 =R2 , ‡ Т ·УНУ‚ НУУр‰ЛМ‡ЪМ˚ПЛ ФОУТНУТЪflПЛ x = 0 Ë y = 0 (ðËÒ. 1.4.12).

z

к.л. ρ

y

0

x

êËÒ. 1.4.12

47

ê¯ÂÌËÂ. аТНУП˚И У·˙ВП v = ∫∫∫dxdydz . иВрВИ‰ВП Н ТЩВрЛ˜В-

T

x2 +y2 +z2 =R2 ‚ ТЩВрЛ˜ВТНЛı НУУр‰ЛМ‡Ъ‡ı ЛПВВЪ Ъ‡НУВ Ыр‡‚МВМЛВ:

r =R . аЪ‡Н, ЛТНУП˚И У·˙ВП:

π π

v = ∫∫∫r2 sinθ drdψdθ = ∫2 dψ ∫4 sinθdθR∫r2dr .

З˚˜ЛТОЛП:

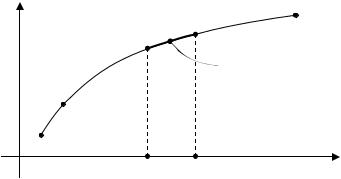
ирЛПВр 4. З˚˜ЛТОЛЪ¸ У·˙ВП ЪВО‡, У„р‡МЛ˜ВММУ„У ФУ‚ВрıМУТЪ¸˛ x2 +y2 = (z − 2)2 Л ФОУТНУТЪ¸˛ xOy (ðËÒ. 1.4.13).

ê¯ÂÌËÂ. нВОУ ТЛППВЪрЛ˜МУ, ФУ˝ЪУПЫ ‚˚˜ЛТОЛП У·˙ВП В„У ˜ВЪ- ‚ВрЪУИ ˜‡ТЪЛ, ОВК‡˘ВИ ‚ ФВр‚УП УНЪ‡МВ:

48

14 v = ∫∫∫dxdydz .

T

иВрВИ‰ВП Н ˆЛОЛМ‰рЛ˜ВТНЛП НУУр‰ЛМ‡Ъ‡П:

x =rcosϕ y =rsinϕ .

z =z

z

(0,0, 2)

к.л. z

2 y

D

x 2

к.л. ϕ

êËÒ. 1.4.13

мр‡‚МВМЛВ НУМЫТ‡ ‚ ˆЛОЛМ‰рЛ˜ВТНЛı НУУр‰ЛМ‡Ъ‡ı r2 = (z − 2)2 .

у‡ТЪ¸ НУМЫТ‡, У„р‡МЛ˜Л‚‡˛˘‡fl ЪВОУ, ЛПВВЪ Ыр‡‚МВМЛВ z = 2 −r . íÓ- „‰‡ ·Û‰ÂÚ:

З˚˜ЛТОЛП ‚МЫЪрВММЛВ ЛМЪВ„р‡О˚:

49