
Госы 5к Надя / лекции_3 / kr-int
.pdf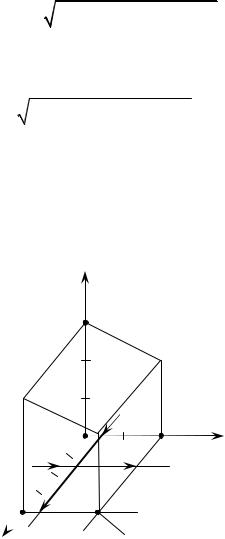
б‡ПВЪЛП, ˜ЪУ Dk fl‚ОflВЪТfl УрЪУ„УМ‡О¸МУИ ФрУВНˆЛВИ ФОУ˘‡‰НЛ Tk (ðËÒ. 1.1.13). аı ФОУ˘‡‰Л Т‚flБ‡М˚ ТУУЪМУ¯ВМЛВП:
Fk = Sk cosϕk ,
„‰Â ϕk – ÓÒÚð˚È Û„ÓÎ ÏÂÊ‰Û ÔÎÓ˘‡‰Í‡ÏË Dk Ë Tk . çÓ Û„ÓÎ ÏÂʉÛ
‰‚ЫПfl ФОУТНУТЪflПЛ р‡‚ВМ Ы„ОЫ ПВК‰Ы МУрП‡ОflПЛ Н МЛП, Ъ.В.
ϕk =νk ,
„‰Â νk – УТЪр˚И Ы„УО ПВК‰Ы МУрП‡О¸˛ Н ФУ‚ВрıМУТЪЛ S Ë ÓÒ¸˛ Oz . íÓ„‰‡ ÔÓÎÛ˜ËÏ
S = |
Fk |
= p2 (x,y) +q2 (x,y) +1 |
F . |
|
|||
k |
cosνk |
k |
|
|
|
||
лЫППЛрЫfl ‚ТВ Ъ‡НЛВ ˝ОВПВМЪ‡рМ˚В ФОУ˘‡‰Л Л ЫТЪрВПОflfl р‡М„ ‰рУ·ОВМЛfl λ Í ÌÛβ, ÔÓÎÛ˜ËÏ ÓÍÓ̘‡ÚÂθÌÓ:
S = ∫∫ p2 (x,y) +q2 (x,y) +1 dxdy .
|
D |
|
|
|
ирЛПВр 4. |
З˚˜ЛТОЛЪ¸ |
ÔÎÓ˘‡‰¸ |
˜‡ÒÚË |
ФУ‚ВрıМУТЪЛ |
S : 2z +y −6 = 0 , |
р‡ТФУОУКВММ˚И М‡‰ У·О‡ТЪ¸˛ D , |
У„р‡МЛ˜ВММУИ |
||
ÔðflÏ˚ÏË x = 0 , x = 4 , y = 0 , y = 2 , ОВК‡˘ЛПЛ ‚ ФОУТНУТЪЛ xOy .
z
(0,0,3)
S
|
0 |
|
|
(0, 2,0) |
|
|
|
|
y |
||
|
|
D |
|
||
|
|
|
|
|
|
(4,0,0) |
|
|
|
x = 4 |
|
x |
|
|
|
||
y = 2 (4, 2,0) |
|||||
|
|||||
|
êËÒ. 1.1.14 |
|
|||
ê¯ÂÌËÂ. СОfl М‡ıУК‰ВМЛfl ФОУ˘‡‰Л НЫТН‡ ФОУТНУТЪЛ S , р‡ТФУОУКВММУ„У М‡‰ У·О‡ТЪ¸˛ D (рЛТ. 1.1.14), ‚УТФУО¸БЫВПТfl ‚˚‚В‰ВММУИ ЩУрПЫОУИ ‰Оfl ФОУ˘‡‰Л НрЛ‚УИ ФУ‚ВрıМУТЪЛ:
21

S = ∫∫ p2 (x,y) +q2 (x,y) +1 dxdy .
D
З М‡¯ВП ТОЫ˜‡В Ыр‡‚МВМЛВ ФУ‚ВрıМУТЪЛ S ПУКМУ Б‡ФЛТ‡Ъ¸ Ъ‡Н: z = 3 − 12 y, ÚÓ„‰‡
p(x,y) = ∂∂xz = 0, q(x,y) = ∂∂yz = −0,5 .
ëΉӂ‡ÚÂθÌÓ,
S = p2 (x,y) +q2 (x,y) +1 = 0,52 +1 = 1, 25 = 0,5 5 .
оУрПЛрЫВП ЛМЪВ„р‡О:
S = ∫∫0,5 5 dxdy = 0,5 5 ∫∫dxdy ;
|
D |
|
D |
|||
∫∫dxdy = ∫4 dx∫2 dy; |
|
|
||||
D |
0 0 |
|
|
|
|
|
Iвнутр = ∫2 dy =y |
|
02 = 2; |
|
|
||
|
|
|
||||
|
|
|
||||
|
0 |
|
|
|
|
|
|
4 |
|
|
4 |
|
|
S = 0,5 5 ∫2dx = 5 x |
= 4 5 . |
|||||
0 |
||||||
|
0 |
|
|
|
|
|
аЪ‡Н, ЛТНУП‡fl ФОУ˘‡‰¸ НЫТН‡ ФОУТНУТЪЛ S («Нр˚¯‡»), р‡ТФУОУКВММУИ М‡‰ У·О‡ТЪ¸˛ D («ÔÓλ), ð‡‚̇ S = 4 5 .
§2. нрУИМУИ ЛМЪВ„р‡О
1. йФрВ‰ВОВМЛВ ЪрУИМУ„У ЛМЪВ„р‡О‡.
к‡ТТПУЪрЛП МВНУЪУрЫ˛ ФУ‚ВрıМУТЪ¸ S .
йФрВ‰ВОВМЛВ 1. èÓ‚ÂðıÌÓÒÚ¸ S ̇Á˚‚‡ÂÚÒfl ФрУТЪУИ ФУ‚ВрıМУТЪ¸˛, ВТОЛ УМ‡ р‡ТФ‡‰‡ВЪТfl М‡ НУМВ˜МУВ ˜ЛТОУ ˜‡ТЪВИ, ЛПВ˛- ˘Лı Ыр‡‚МВМЛВ z = f(x,y) , ËÎË x =ψ(y,z) , ËÎË y =η(x,z) , Ôð˘ÂÏ ÙÛÌ͈ËË f(x,y) , ψ(y,z) Ë ψ(y,z) МВФрВр˚‚М˚ ‚ МВНУЪУрУИ ФрУТЪУИ У·О‡ТЪЛ D .
З ‰‡О¸МВИ¯ВП П˚ ·Ы‰ВП р‡ТТП‡ЪрЛ‚‡Ъ¸ ФрУТЪр‡МТЪ‚ВММ˚В У·О‡Т- ЪЛ, У„р‡МЛ˜ВММ˚В ФрУТЪ˚ПЛ ФУ‚ВрıМУТЪflПЛ.
22

мЪУ˜МЛП ЪВФВр¸ ФУМflЪЛВ У·˙ВП‡ ЪВО‡ T , У„р‡МЛ˜ВММУ„У ФрУТЪУИ ФУ‚ВрıМУТЪ¸˛ S . СОfl ˝ЪУ„У ФУПВТЪЛП ЪВОУ T ˆВОЛНУП ‚МЫЪр¸ Ф‡- р‡ООВОВФЛФВ‰‡, „р‡МЛ НУЪУрУ„У Ф‡р‡ООВО¸М˚ НУУр‰ЛМ‡ЪМ˚П ФОУТНУТЪflП xOy , xOz Ë yOz . к‡БУ·¸ВП ‰‡ОВВ Ф‡р‡ООВОВФЛФВ‰ ФОУТНУТЪflПЛ, Ф‡р‡ООВО¸М˚ПЛ НУУр‰ЛМ‡ЪМ˚П ФОУТНУТЪflП, М‡ fl˜ВИНЛ. й·У- БМ‡˜ЛП ˜ВрВБ A ТЫППЫ У·˙ВПУ‚ fl˜ВВН, ˆВОЛНУП ОВК‡˘Лı ‚МЫЪрЛ ЪВО‡ T Ë Ì Ëϲ˘Ëı ÌË Ó‰ÌÓÈ Ó·˘ÂÈ ÚÓ˜ÍË Ò ÔÓ‚ÂðıÌÓÒÚ¸˛ S , Ó„ð‡Ì˘˂‡˛˘ÂÈ ÚÂÎÓ T . é·ÓÁ̇˜ËÏ ˜ÂðÂÁ B ТЫППЫ У·˙ВПУ‚ fl˜В- ВН, ЛПВ˛˘Лı Т ЪВОУП T ËÎË Â„Ó ÔÓ‚ÂðıÌÓÒÚ¸˛ ıÓÚfl ·˚ Ó‰ÌÛ Ó·˘Û˛ ÚÓ˜ÍÛ. é˜Â‚ˉÌÓ, ˜ÚÓ A≤B . з‡Л·УО¸¯ЛИ ЛБ ‰Л‡ПВЪрУ‚ fl˜ВВН М‡- БУ‚ВП р‡М„УП ‰рУ·ОВМЛfl λ . ÖÒÎË ÒÛ˘ÂÒÚ‚ÛÂÚ Ó·˘Â Á̇˜ÂÌËÂ
limA= limB =v
λ→∞ λ→∞
ФрЛ ЫТОУ‚ЛЛ, ˜ЪУ ˜ЛТОУ fl˜ВВН ·ВТНУМВ˜МУ Ы‚ВОЛ˜Л‚‡ВЪТfl, ‡ р‡М„ ‰рУ·ОВМЛfl ТЪрВПЛЪТfl Н МЫО˛, ЪУ ˜ЛТОУ v ̇Á˚‚‡ÂÚÒfl Ó·˙ÂÏÓÏ ÚÂ- · T , ‡ Ò‡ÏÓ ÚÂÎÓ Ì‡Á˚‚‡ÂÚÒfl НЫ·ЛрЫВП˚П.
á‡Ï˜‡ÌËÂ. б‡ПВЪЛП, ˜ЪУ р‡МВВ П˚ ‡М‡ОУ„Л˜МУ УФрВ‰ВОЛОЛ ФОУ˘‡‰¸ ФОУТНУИ У·О‡ТЪЛ.
С‡‰ЛП ЪВФВр¸ УФрВ‰ВОВМЛВ ЪрУИМУ„У ЛМЪВ„р‡О‡.
к‡ТТПУЪрЛП МВНУЪУрУВ ЪВОУ T , У„р‡МЛ˜ВММУВ ФрУТЪУИ ФУ‚ВрıМУТЪ¸˛ (рЛТ. 1.2.1). еУКМУ ‰УН‡Б‡Ъ¸, ˜ЪУ Ъ‡НЛВ ЪВО‡ НЫ·ЛрЫВП˚, Ъ.В. ЛПВ˛Ъ У·˙ВП. а ФЫТЪ¸ ‚ Н‡К‰УИ ЪУ˜НВ ˝ЪУ„У ЪВО‡ Б‡‰‡М‡ ЩЫМНˆЛfl f(x,y,z) .
z |
z =z2 (x,y) |
|
T |
0 |
y z =z (x,y) |
|
1 |
D |
y =y2 (x) |
|
x
y =y1(x)
êËÒ. 1.2.1
23
йФрВ‰ВОВМЛВ 2 (УФрВ‰ВОВМЛВ ЪрУИМУ„У ЛМЪВ„р‡О‡). ê‡ÁÓ·¸ÂÏ ÚÂÎÓ T ФрУТЪ˚ПЛ ФУ‚ВрıМУТЪflПЛ М‡ ˜‡ТЪЛ T1 , T2 , ..., Tn Ò ‰Ë‡ÏÂÚ- ð‡ÏË d1 , d2 , ..., dn Ë Ó·˙ÂχÏË v1 , v2 , ..., vn . з‡Л·УО¸¯ЛИ ЛБ ‰Л‡ПВЪрУ‚ dk ̇Á˚‚‡ÂÚÒfl ð‡Ì„ÓÏ ‰ðÓ·ÎÂÌËfl λ .
Ç Í‡Ê‰ÓÈ ˜‡ÒÚ˘ÌÓÈ fl˜ÂÈÍ Tk ‚УБ¸ПВП ФрУЛБ‚УО¸МЫ˛ ЪУ˜НЫ
Mk (xk ,yk ,zk ) Л ‚˚˜ЛТОЛП ‚ МВИ БМ‡˜ВМЛВ ЩЫМНˆЛЛ f(xk ,yk ,zk ) , НУЪУрУВ ЫПМУКЛП М‡ У·˙ВП ТУУЪ‚ВЪТЪ‚Ы˛˘ВИ fl˜ВИНЛ vk , Ú.Â. ÒÓÒÚ‡-
‚ЛП ФрУЛБ‚В‰ВМЛВ: f(xk ,yk ,zk ) vk .
ирУТЫППЛрЫВП ‚ТВ Ъ‡НЛВ ФрУЛБ‚В‰ВМЛfl, Ъ.В. ТУТЪ‡‚ЛП ЛМЪВ- „р‡О¸МЫ˛ ТЫППЫ (ТЫППЫ кЛП‡М‡):
n
σn = ∑f(xk ,yk ,zk ) vk . k=1
аБПВО¸˜‡fl ‰рУ·ОВМЛВ, ·Ы‰ВП ЛТН‡Ъ¸ ФрВ‰ВО ФУТОВ‰У‚‡ЪВО¸МУТЪЛ ЛМЪВ„р‡О¸М˚ı ТЫПП
I = limσn .
n→∞
λ→0
ЦТОЛ ˝ЪУЪ ФрВ‰ВО ТЫ˘ВТЪ‚ЫВЪ Л МВ Б‡‚ЛТЛЪ УЪ ТФУТУ·‡ ‰рУ·ОВМЛfl Л ‚˚·Ур‡ ЪУ˜ВН Mk , ÚÓ ÓÌ Ì‡Á˚‚‡ÂÚÒfl ЪрУИМ˚П ЛМЪВ„р‡ОУП ÓÚ
ÙÛÌ͈ËË f(x,y,z) ÔÓ ÚÂÎÛ T Ë Ó·ÓÁ̇˜‡ÂÚÒfl Ú‡Í:
I = ∫∫∫f(x,y,z) dxdydz
T
ËÎË
I = ∫∫∫f(M) dv .
T
аЪ‡Н, О‡НУМЛ˜МУ ПУКМУ ТН‡Б‡Ъ¸ Ъ‡Н: ЪрУИМУИ ЛМЪВ„р‡О ВТЪ¸ ФрВ‰ВО ФУТОВ‰У‚‡ЪВО¸МУТЪЛ ЛМЪВ„р‡О¸М˚ı ТЫПП, Ъ.В.:
|
def |
n |
I = ∫∫∫f(x,y,z) dxdydz = nlim→∞ |
∑f(xk ,yk ,zk ) vk |
|
T |
λ→0 |
k=1 |
нВУрВП‡ ТЫ˘ВТЪ‚У‚‡МЛfl ЪрУИМУ„У ЛМЪВ„р‡О‡. ÖÒÎË ÙÛÌ͈Ëfl f(x,y,z) МВФрВр˚‚М‡ ‚ Н‡К‰УИ ЪУ˜НВ ЪВО‡ T , Ó„ð‡Ì˘ÂÌÌÓ„Ó ÔðÓ-
ТЪУИ ФУ‚ВрıМУТЪ¸˛, ЪУ ТЫ˘ВТЪ‚ЫВЪ ЪрУИМУИ ЛМЪВ„р‡О УЪ ЩЫМНˆЛЛ f(x,y,z) ÔÓ ÚÂÎÛ T .
(ÅÂÁ ‰Ó͇Á‡ÚÂθÒÚ‚‡.)
24
б‡ПВЪЛП, ˜ЪУ Т‚УИТЪ‚‡ ЪрУИМУ„У ЛМЪВ„р‡О‡ ‡М‡ОУ„Л˜М˚ Т‚УИТЪ- ‚‡П ‰‚УИМУ„У ЛМЪВ„р‡О‡, ФУ˝ЪУПЫ П˚ МВ ·Ы‰ВП М‡ МЛı УЪ‰ВО¸МУ УТ- Ъ‡М‡‚ОЛ‚‡Ъ¸Тfl.
2. З˚˜ЛТОВМЛВ ЪрУИМУ„У ЛМЪВ„р‡О‡.
èÛÒÚ¸ ÚÂÎÓ T ВТЪ¸ ФрУТЪ‡fl У·О‡ТЪ¸ (рЛТ. 1.2.1). СУФЫТЪЛП, ˜ЪУ УМУ У„р‡МЛ˜ВМУ ТМЛБЫ ФУ‚ВрıМУТЪ¸˛ z =z1(x,y) , Ò‚ÂðıÛ ÔÓ‚ÂðıÌÓÒÚ¸˛ z =z2 (x,y) , ‡ Т ·УНУ‚ – ˆЛОЛМ‰рЛ˜ВТНУИ ФУ‚ВрıМУТЪ¸˛, У·р‡- БЫ˛˘ЛВ НУЪУрУИ Ф‡р‡ООВО¸М˚ УТЛ Oz , ‡ М‡Фр‡‚Оfl˛˘ВИ ТОЫКЛЪ „р‡МЛˆ‡ ФрУТЪУИ У·О‡ТЪЛ D , р‡ТФУОУКВММУИ ‚ ФОУТНУТЪЛ xOy , Ôð˘ÂÏ ÙÛÌ͈ËË z1(x,y) Ë z2 (x,y) МВФрВр˚‚М˚ ‚ У·О‡ТЪЛ D . иЫТЪ¸, НрУПВ ЪУ„У, ЩЫМНˆЛfl f(x,y,z) ЛМЪВ„рЛрЫВП‡ ‚ ЪВОВ T .
нУ„‰‡ ПУКМУ М‡ФЛТ‡Ъ¸
|
z2 |
(x,y) |
|
∫∫∫f(x,y,z) dxdydz = ∫∫ |
∫ |
f(x,y,z)dz dxdy, |
|
T |
1 |
|
|
D z (x,y) |
|
||
Ôð˘ÂÏ ËÌÚ„ð‡Î, ÒÚÓfl˘ËÈ ÒÔð‡‚‡, Á‡ÔËÒ˚‚‡ÂÚÒfl Ú‡Í:
∫∫∫f(x,y,z) dxdydz = ∫∫dxdy |
z2 (x,y) |
|
∫ f(x,y,z)dz . |
||
T |
D |
z1 (x,y) |
Ç ÚÓÏ ÒÎÛ˜‡Â, ÍÓ„‰‡ ӷ·ÒÚ¸ |
D У„р‡МЛ˜ВМ‡ ТМЛБЫ МВФрВр˚‚МУИ |
|
ÍðË‚ÓÈ y =y1(x) , Т‚ВрıЫ – МВФрВр˚‚МУИ НрЛ‚УИ y =y2 (x) , ‡ Ò ·ÓÍÓ‚
ÔðflÏ˚ÏË x =a |
Ë x =b , ЪУ ФУТОВ‰М˛˛ ЩУрПЫОЫ ПУКМУ Б‡ФЛТ‡Ъ¸ |
||
Ú‡Í: |
|
|
|
|
b |
y2 (x) |
z2 (x,y) |
∫∫∫f(x,y,z) dxdydz = ∫dx |
∫ dy |
∫ f(x,y,z)dz . |
|
T |
a |
y1 (x) |
z1 (x,y) |
аМЪВ„р‡О, ТЪУfl˘ЛИ ТФр‡‚‡, М‡Б˚‚‡ВЪТfl ЪрВıНр‡ЪМ˚П ЛОЛ ФУ‚ЪУр- М˚П. б‡ПВЪЛП, ˜ЪУ ‚˚·Лр‡fl ‚МВ¯МВВ ЛМЪВ„рЛрУ‚‡МЛВ ФУ ФВрВПВММУИ y ËÎË z , ПУКМУ М‡ФЛТ‡Ъ¸ В˘В ФflЪ¸ р‡БОЛ˜М˚ı ЪрВıНр‡ЪМ˚ı ЛМЪВ„р‡ОУ‚, ˜ВрВБ НУЪУр˚В ‚˚р‡К‡ВЪТfl ‰‡ММ˚И ЛМЪВ„р‡О I . иУрfl- ‰УН ‚˚ФУОМВМЛfl УФВр‡ˆЛИ ЛМЪВ„рЛрУ‚‡МЛfl Б‡‚ЛТЛЪ УЪ ‚Л‰‡ У·О‡Т- ЪЛ, ФУ НУЪУрУИ ‚˚ФУОМflВЪТfl ЛМЪВ„рЛрУ‚‡МЛВ.
25

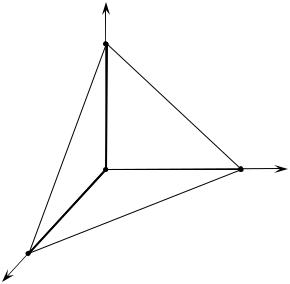
3. ЙВУПВЪрЛ˜ВТНЛИ ТП˚ТО ЪрУИМУ„У ЛМЪВ„р‡О‡.
Ç ÚÓÏ ÒÎÛ˜‡Â, ÍÓ„‰‡ ÔÓ‰˚ÌÚ„ð‡Î¸Ì‡fl ÙÛÌ͈Ëfl f(x,y,z) =1, ЪУ У˜В‚Л‰МУ, ˜ЪУ ЪрУИМУИ ЛМЪВ„р‡О I = ∫∫∫dxdydz ‰‡ÂÚ Ì‡Ï Ó·˙ÂÏ Ú·
T
T , ФУ НУЪУрУПЫ ‚В‰ВЪТfl ЛМЪВ„рЛрУ‚‡МЛВ.
z
2
T
|
y |
D |
1 |
x 1 (1,1) |
D1 |
êËÒ. 1.2.2
ирЛПВр 1. З˚˜ЛТОЛЪ¸ У·˙ВП ЪВО‡, У„р‡МЛ˜ВММУ„У ФУ‚ВрıМУТЪflПЛ z = 2 −x2 −y2 , z = 0, x = ±1, y = ±1.
ê¯ÂÌËÂ. é˜Â‚ˉÌÓ, ˜ÚÓ ‰‡ÌÌÓ ÚÂÎÓ Ôð‰ÒÚ‡‚ÎflÂÚ ÒÓ·Ó˛ ¯‡ÚÂð, Ó„ð‡Ì˘ÂÌÌ˚È Ò‚ÂðıÛ Ô‡ð‡·ÓÎÓˉÓÏ ‚ð‡˘ÂÌËfl z = 2 −x2 −y2 . ирЛ- ˜ВП ˝Ъ‡ ФУ‚ВрıМУТЪ¸ ТЛППВЪрЛ˜М‡ УЪМУТЛЪВО¸МУ НУУр‰ЛМ‡ЪМ˚ı ФОУТНУТЪВИ xOz Ë yOz . C ·УНУ‚ ФОУТНУТЪЛ x =1, x = −1, y =1, Ë y = −1 ТрВБ‡˛Ъ Т Ф‡р‡·УОУЛ‰‡ ТЛППВЪрЛ˜М˚В „Ур·Ы¯НЛ, У·р‡БЫfl ˜В- Ъ˚рВ ‡рНЛ (рЛТ. 1.2.2). лМЛБЫ ЪВОУ У„р‡МЛ˜ВМУ Н‚‡‰р‡ЪУП, У„р‡МЛ- ˜ВММ˚П ФрflП˚ПЛ x = ±1 Ë y = ±1.
й˜В‚Л‰МУ, ˜ЪУ ЛТНУП˚И У·˙ВП
|
|
|
|
|
|
2−x2 −y2 |
1 |
|
1 |
|
|
|
2−x2 −y2 |
|
|
|
|
||
vT = ∫∫∫dxdydz = ∫∫dxdy |
|
∫ |
dz = ∫dx∫dy |
∫ dz = |
|
|
|||||||||||||
T |
|
|
D |
|
0 |
|
−1 |
|
−1 |
0 |
|
|
|
|
|||||
2−x2 −y2 |
|
|
|
02−x2 −y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 внутр = ∫ |
dz =z |
|
|
= 2 −x2 −y2 . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
−x2 )y − y |
3 |
|
|
1 |
= |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
I2 внутр = ∫(2 −x2 −y2 )dy = |
(2 |
|
|
|
|
|
|
|
|
||||||||||
−1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= (2 −x2 ) 1 |
− 1 |
|
− (2 −x |
2 ) (−1) + 1 |
= |
2 (2 −x2 ) − |
2 |
= |
10 |
− 2x2 . |
|||||||||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
3 |
|
||
26
éÍÓ̘‡ÚÂθÌÓ, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
10 |
− 2x |
2 |
|
|
10x |
|
2x3 |
|
1 |
|
10 |
|
2 |
|
10 |
|
2 |
|
|
20 |
|
4 |
|
16 |
||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
vT = |
|
3 |
|
dx = |
3 |
− |
|
|
|
|
= |
3 |
− |
3 |
− |
− |
3 |
+ |
3 |
|
= |
3 |
− |
3 |
= |
3 |
||
|
|
|
|
|||||||||||||||||||||||||
−∫1 |
|
|
|
|
|
|
3 |
|
−1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
v |
= 16 ÍÛ·. ‰. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
T |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б‡ПВЪЛП, ˜ЪУ ‰‡ММУВ ЪВОУ ТЛППВЪрЛ˜МУ УЪМУТЛЪВО¸МУ НУУр‰Л- М‡ЪМ˚ı ФОУТНУТЪВИ, ФУ˝ЪУПЫ ПУКМУ ЫФрУТЪЛЪ¸ рВ¯ВМЛВ, ‚˚˜ЛТОЛ‚
14 У·˙ВП‡. Д ЛПВММУ:
14 vT = ∫∫dxdy |
2−x2 −y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
||||||
∫ |
dz = ∫∫(2 −x2 −y2 )dxdy = ∫dx |
∫(2 −x2 −y2 )dy |
|||||||||||||||||||||||||
|
|
|
D1 |
|
|
0 |
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
= 2 −x2 − |
1 |
= |
5 |
−x2 . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Iвнутр = ∫(2 −x2 −y2 )dy = (2 −x2 )y − y |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
0 |
|
|
|
3 |
|
3 |
|
||
1 |
|
|
1 |
5 |
|
|
|
5 |
x3 |
|
1 |
5 |
|
1 |
|
4 |
|
|
|
|
|
|
|||||
vT |
= |
|
−x |
2 |
x − |
|
− |
= |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
4 |
∫0 |
|
3 |
dx |
= |
3 |
|
|
= |
3 |
|
3 |
3 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
3 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= 16 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
éÚÍÛ‰‡ ÒΉÛÂÚ, ˜ÚÓ v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
T |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ирЛПВр 2. З˚˜ЛТОЛЪ¸ У·˙ВП ЪВО‡, У„р‡МЛ˜ВММУ„У НУУр‰ЛМ‡ЪМ˚- ПЛ ФУ‚ВрıМУТЪflПЛ Л ФОУТНУТЪ¸˛ x +y +z −1 = 0 (ðËÒ. 1.2.3).
z
|
|
|
1 |
|
|
y +z −1 = 0 |
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
x +z −1 = 0 |
|
T |
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Dyz |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
Dxz |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
Dxy |
|
|
||||||
|
|
x +y −1 = 0 |
||||||||
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
êËÒ. 1.2.3 |
|
|
||||||
27
ê¯ÂÌËÂ. аТНУП˚И У·˙ВП ЪВО‡, ФрВ‰ТЪ‡‚Оfl˛˘В„У ТУ·УИ ФЛр‡ПЛ- ‰Ы, У„р‡МЛ˜ВММЫ˛ НУУр‰ЛМ‡ЪМ˚ПЛ ФОУТНУТЪflПЛ Л ФОУТНУТЪ¸˛ x +y +z −1 = 0 , П˚ М‡¯ОЛ р‡МВВ, ‚˚р‡БЛ‚ В„У ˜ВрВБ ‰‚УИМУИ ЛМЪВ- „р‡О.
й˜В‚Л‰МУ, ˜ЪУ В„У ПУКМУ М‡ИЪЛ Л ˜ВрВБ ЪрУИМУИ ЛМЪВ„р‡О. Д
ЛПВММУ:
vT = ∫∫∫dxdydz
T
иВрВИ‰fl Н ЪрВıНр‡ЪМУПЫ ЛМЪВ„р‡ОЫ, П˚ ПУКВП ˝ЪУ Т‰ВО‡Ъ¸ ¯В- ТЪ¸˛ р‡БОЛ˜М˚ПЛ ТФУТУ·‡ПЛ, ‡ ЛПВММУ:
|
1−x−y |
1 |
1−x |
1−x−y |
1 |
1−y |
1−x−y |
|
vT = ∫∫dxdy |
∫ |
dz = ∫dx |
∫dy ∫ |
dz = ∫dy ∫dx ∫ |
dz , |
|||
Dxy |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
ËÎË |
|
|
|
|
|
|
1−y−z |
1 |
1−y |
1−y−z |
1 |
1−z |
1−y−z |
|
vT = ∫∫dydz |
∫ |
dx = ∫dy |
∫dz |
∫ dx = ∫dz |
∫dy |
∫ |
dx , |
|
Dyz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
ËÎË |
|
|
|
|
|
vT = ∫∫dxdz1−x∫−zdx = ∫1 dx |
1−∫xdz1−x∫−zdy = ∫1 dz1−∫zdx |
1−x∫−zdy . |
||||||
Dxz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
ирЛ‚В‰ВП ‚˚˜ЛТОВМЛВ ФУ ФУТОВ‰МВИ ЩУрПЫОВ (МВ ЪрЫ‰МУ Ы·В- ‰ЛЪ¸Тfl, ˜ЪУ УТЪ‡О¸М˚В ЛМЪВ„р‡О˚ ‚˚˜ЛТОfl˛ЪТfl ‡М‡ОУ„Л˜МУ). аПВ-
ÂÏ:
vT = ∫1 dz1−∫zdx1−x∫−zdy ,
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 внутр = |
1−x∫−zdy =y |
|
10−x−z =1−x −z , |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−z |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1−z |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
(1−x −z)dx = x − x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
I1 внутр = ∫ |
|
|
−zx |
|
|
= |
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
(1−z)2 |
|
|
|
(1−z)2 |
|
|
|
|||||||||||
|
|
|
|
|
= |
(1−z) − |
|
−z(1−z) = |
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
éÍÓ̘‡ÚÂθÌÓ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
(1 |
−z) |
2 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
vT = ∫ |
|
dz = |
∫(1− 2z +z2 )dz = 1 |
z −z2 |
+ z |
|
|
|
|
= |
ÍÛ·. ‰. |
||||||||||||||
|
2 |
|
2 |
|
6 |
||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
2 |
|
|
3 |
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
28

§3. ирЛОУКВМЛfl ‰‚УИМ˚ı Л ЪрУИМ˚ı ЛМЪВ„р‡ОУ‚
1. З˚˜ЛТОВМЛВ ФОУ˘‡‰Л ФОУТНУИ У·О‡ТЪЛ D .
|
y |
|
y =y2 (x) |
|
d |
|
|
|
x =x2 (y) |
|
|
|
|
y =y1(x) |
x =x1(y) |
|
D |
|
|
|
|
|
|
|
c |
|
|
|
|
0 |
a |
b |
x |
|
êËÒ. 1.3.1
е˚ ЫТЪ‡МУ‚ЛОЛ, ˜ЪУ ФОУ˘‡‰¸ ФОУТНУИ У·О‡ТЪЛ D , У„р‡МЛ˜ВММУИ ФрУТЪУИ НрЛ‚УИ, ОВК‡˘ВИ ‚ У·О‡ТЪЛ D , ПУКМУ ‚˚˜ЛТОЛЪ¸ Т ФУПУ- ˘¸˛ ‰‚УИМУ„У ЛМЪВ„р‡О‡, ФрЛ˜ВП ФВрВИЪЛ Н ФУ‚ЪУрМУПЫ ЛМЪВ„р‡ОЫ ПУКМУ ‰‚ЫПfl р‡БОЛ˜М˚ПЛ ТФУТУ·‡ПЛ (рЛТ. 1.3.1):
|
b |
y2 (x) |
|
SD = ∫∫dxdy = ∫dx ∫ |
dy |
||
D |
a |
y1 (x) |
|
ËÎË |
|
|
|
|
d |
x2 (y) |
|
SD = ∫∫dxdy = ∫dy |
∫ |
dx . |
|
D |
c |
x1 (y) |
|
2. З˚˜ЛТОВМЛВ ФОУ˘‡‰Л НрЛ‚УИ ФУ‚ВрıМУТЪЛ.
к‡МВВ П˚ ЫТЪ‡МУ‚ЛОЛ, ˜ЪУ ФОУ˘‡‰¸ НрЛ‚УИ ФУ‚ВрıМУТЪЛ S , Б‡- ‰‡ММУИ Ыр‡‚МВМЛВП z = f(x,y) Л р‡ТФУОУКВММУИ М‡‰ У·О‡ТЪ¸˛ D ‚ ФОУТНУТЪЛ xOy , ‚˚˜ЛТОflВЪТfl ФУ ЩУрПЫОВ:
|
S = ∫∫ |
p2 (x,y) +q2 (x,y) +1 dxdy (ðËÒ. 1.1.12), |
|
|
D |
|
|
„‰Â p(x,y) = |
∂z(x,y) |
, q(x,y) = |
∂z(x,y) . |
|
∂x |
|
∂y |
29
3. З˚˜ЛТОВМЛВ У·˙ВП‡ ЪВО‡ T .
z S : z = f(x,y)
0 |
y |
T |
|
x |
D |
|
|
|
êËÒ. 1.3.2 |
ÖÒÎË ÚÂÎÓ T У„р‡МЛ˜ВМУ ТМЛБЫ ФрУТЪУИ У·О‡ТЪ¸˛ D , Ò‚ÂðıÛ – |
|
ÔÓ‚ÂðıÌÓÒÚ¸˛ z = f(x,y) |
( f(x,y) ≥ 0), Т ·УНУ‚ ˆЛОЛМ‰рЛ˜ВТНУИ ФУ- |
‚ВрıМУТЪ¸˛, У·р‡БЫ˛˘ЛВ НУЪУрУИ Ф‡р‡ООВО¸М˚ УТЛ Oz , ‡ М‡Фр‡‚- Оfl˛˘ВИ ТОЫКЛЪ НУМЪЫр У·О‡ТЪЛ D , ЪУ„‰‡ У·˙ВП ЪВО‡ ПУКМУ ‚˚-
˜ЛТОЛЪ¸ Т ФУПУ˘¸˛ ‰‚УИМУ„У ЛМЪВ„р‡О‡ Ъ‡Н:
vT = ∫∫f(x,y)dxdy (ðËÒ. 1.3.2)
D
ЛОЛ Т ФУПУ˘¸˛ ЪрУИМУ„У ЛМЪВ„р‡О‡ ТУУЪ‚ВЪТЪ‚ВММУ: vT = ∫∫∫dxdydz .
|
T |
4. З˚˜ЛТОВМЛВ П‡ТТ˚ ФУ‚ВрıМУТЪЛ. |
|
èÛÒÚ¸ ‚ ͇ʉÓÈ ÚӘ͠|
ФУ‚ВрıМУТЪЛ S , Б‡‰‡ММУИ Ыр‡‚МВМЛВП |
z = f(x,y) , ФОУЪМУТЪ¸ р‡‚М‡ |
ρ(x,y,z), „‰Â ρ(x,y,z) – МВФрВр˚‚М‡fl |
ЩЫМНˆЛfl ‚ Н‡К‰УИ ЪУ˜НВ ФУ‚ВрıМУТЪЛ S , ‡ ÙÛÌ͈Ëfl f(x,y) МВФрВ- р˚‚М‡ ‚ У·О‡ТЪЛ D ФОУТНУТЪЛ xOy Л ЛПВВЪ ‚ МВИ ˜‡ТЪМ˚В ФрУЛБ- ‚У‰М˚В
|
∂z(x,y) |
= p(x,y) |
Ë |
∂z(x,y) |
=q(x,y) . |
|
|
|
|
|
|||
|
∂x |
|
∂y |
|
||
к‡Б·Л‚‡fl ФрУЛБ‚УО¸М˚П У·р‡БУП |
ÔÓ‚ÂðıÌÓÒÚ¸ S ̇ n |
˜‡ÒÚÂÈ, |
||||
Б‡ПВЪЛП, ˜ЪУ mk χÒÒ‡ k -È |
fl˜ВИНЛ ФрЛ·ОЛБЛЪВО¸МУ |
ð‡‚̇ |
||||
30
