
Госы 5к Надя / лекции_3 / kr-int
.pdf
ÒÚ‚ÂÌÌÓ, ÚÓ ‚ ӷ·ÒÚË D М‡И‰ВЪТfl МВНУЪУр‡fl ЪУ˜Н‡ P(ξ,η) ڇ͇fl, ˜ÚÓ
S1 ∫∫f(x,y)dxdy = f(ξ,η) ,
D D
ÓÚÍÛ‰‡ ÒΉÛÂÚ, ˜ÚÓ ∫∫f(x,y)dxdy = f(ξ,η) SD .
D
á̇˜ÂÌË f(ξ,η) М‡Б˚‚‡˛Ъ «ТрВ‰МЛП» БМ‡˜ВМЛВП ЩЫМНˆЛЛ ‚ У·- О‡ТЪЛ D .
4. З˚˜ЛТОВМЛВ ‰‚УИМУ„У ЛМЪВ„р‡О‡.
З˚˜ЛТОЛП ‰‚УИМУИ ЛМЪВ„р‡О I = ∫∫f(x,y)dxdy ‚ ФрВ‰ФУОУКВМЛЛ,
D
˜ÚÓ ÙÛÌ͈Ëfl f(x,y) ФУОУКЛЪВО¸М‡ ‚ У·О‡ТЪЛ D , ‡ ӷ·ÒÚ¸ D У„- р‡МЛ˜ВМ‡ ТМЛБЫ НрЛ‚УИ y =y1(x) , Ò‚ÂðıÛ ÍðË‚ÓÈ y =y2 (x) (ðËÒ. 1.1.7), Ôð˘ÂÏ x [a,b] . å˚ Ôð‰ÔÓ·„‡ÂÏ, ˜ÚÓ ÙÛÌ͈ËË y1(x) Ë y2 (x) МВФрВр˚‚М˚ М‡ ФрУПВКЫЪНВ [a,b] Ë ‚ ͇ʉÓÈ Â„Ó ÚӘ͠y1(x) ≤y2 (x) . аБ „ВУПВЪрЛ˜ВТНУ„У ТП˚ТО‡ ‰‚УИМУ„У ЛМЪВ„р‡О‡ flТМУ, ˜ЪУ ‰‚УИМУИ ЛМЪВ„р‡О ∫∫f(x,y)dxdy ‰‡ÂÚ Ì‡Ï Ó·˙ÂÏ Ú·, ËÁÓ·ð‡-
D
КВММУ„У М‡ рЛТ. 1.1.7.
z
|
F(x) |
y |
|
|
|
|
d |
y =y2 (x) |
|
|
|
c |
|
|
0 a x |
x |
y =y1(x) |
b |
êËÒ. 1.1.7
11
з‡И‰ВП У·˙ВП ˝ЪУ„У ЪВО‡ Т ФУПУ˘¸˛ УФрВ‰ВОВММУ„У ЛМЪВ„р‡О‡. СОfl ˝ЪУ„У ФрУ‚В‰ВП ТВ˜ВМЛВ ЪВО‡ ФОУТНУТЪ¸˛ x =const . é·ÓÁ̇˜ËÏ ÔÎÓ˘‡‰¸ ˝ÚÓ„Ó Ò˜ÂÌËfl F(x) . аБ‚ВТЪМУ, ˜ЪУ У·˙ВП ЪВО‡ ФУ ФОУ˘‡-
‰flÏ Ò˜ÂÌËÈ ‚˚˜ËÒÎflÂÚÒfl Ú‡Í:
v = ∫b F(x)dx .
a
éÒÚ‡ÂÚÒfl ̇ÈÚË ÔÎÓ˘‡‰¸ Ò˜ÂÌËfl F(x) . й˜В‚Л‰МУ, ˜ЪУ ˝ЪУ ТВ˜В- МЛВ ФрВ‰ТЪ‡‚ОflВЪ ТУ·У˛ НрЛ‚УОЛМВИМЫ˛ Ър‡ФВˆЛ˛, У„р‡МЛ˜ВММЫ˛
ТМЛБЫ ФрflПУИ x =const , |
Т‚ВрıЫ – НрЛ‚УИ, Ыр‡‚МВМЛВ НУЪУрУИ |
z = f(x,y) (Ôð˘ÂÏ Á‰ÂÒ¸ x |
ЩЛНТЛрУ‚‡МУ), ‡ Т ·УНУ‚ – ФрflП˚ПЛ, |
Ô‡ð‡ÎÎÂθÌ˚ÏË ÓÒË Oz . ëΉӂ‡ÚÂθÌÓ,
y2 (x)
F(x) = ∫ f(x,y)dy .
y1 (x)
иУ‰ТЪ‡‚Оflfl М‡И‰ВММУВ БМ‡˜ВМЛВ F(x) ‚ ËÒıÓ‰Ì˚È ËÌÚ„ð‡Î, ÓÍÓ̘‡ÚÂθÌÓ ÔÓÎÛ˜ËÏ:
|
b y2 (x) |
|
∫∫f(x,y)dxdy = ∫ |
∫ |
|
D |
|
1 |
a y (x) |
||
f(x,y)dy dx .
àÌÚ„ð‡Î, ÒÚÓfl˘ËÈ ‚ Ôð‡‚ÓÈ ˜‡ÒÚË ˝ÚÓ„Ó ð‡‚ÂÌÒÚ‚‡, ̇Á˚‚‡ÂÚÒfl ÔÓ‚ÚÓðÌ˚Ï ËÎË ‰‚ÛÍð‡ÚÌ˚Ï Ë Á‡ÔËÒ˚‚‡ÂÚÒfl Ú‡Í:
b y2 (x) |
|
b |
y2 (x) |
|
∫ |
∫ |
f(x,y)dy dx = ∫dx |
∫ f(x,y)dy . |
|
|
1 |
|
a |
1 |
a y (x) |
|
y (x) |
||
аЪ‡Н, УНУМ˜‡ЪВО¸МУ ФУОЫ˜‡ВП Ъ‡НУВ ‚˚р‡КВМЛВ ‰‚УИМУ„У ЛМЪВ- „р‡О‡ ˜ВрВБ ФУ‚ЪУрМ˚И:
|
b |
y2 (x) |
∫∫f(x,y)dxdy = ∫dx |
∫ f(x,y)dy . |
|
D |
a |
y1 (x) |
|
y2 (x) |
|
б‡ПВЪЛП, ˜ЪУ ЛМЪВ„р‡О |
∫ f(x,y)dy М‡Б˚‚‡ВЪТfl ‚МЫЪрВММЛП, |
|
y1 (x)
ФрЛ ˝ЪУП „У‚УрflЪ, ˜ЪУ ‚МЫЪрВММВВ ЛМЪВ„рЛрУ‚‡МЛВ ‚В‰ВЪТfl ФУ ФВрВПВММУИ y , ‡ ‚МВ¯МВВ – ФУ ФВрВПВММУИ x (ðËÒ. 1.1.7).
ирУ‚У‰fl ТУ‚Вр¯ВММУ ‡М‡ОУ„Л˜М˚В р‡ТТЫК‰ВМЛfl, П˚ ПУКВП ФУОЫ˜ЛЪ¸ ЪУ˜МУ Ъ‡НЫ˛ КВ ЩУрПЫОЫ ‰Оfl ‚˚˜ЛТОВМЛfl ‰‚УИМУ„У ЛМЪВ-
12

„р‡О‡, „‰В ‚МЫЪрВММВВ ЛМЪВ„рЛрУ‚‡МЛВ ‚˚ФУОМВМУ ФУ ФВрВПВММУИ x , ‡ ‚МВ¯МВВ – ФУ ФВрВПВММУИ y :
|
d |
x2 (y) |
∫∫f(x,y)dxdy = ∫dy |
∫ f(x,y)dx . |
|
D |
c |
x1 (y) |
й˜В‚Л‰МУ, ˜ЪУ МВ Л„р‡ВЪ рУОЛ, ФУ Н‡НУИ ФВрВПВММУИ ‚˚ФУОМflВЪТfl ‚МЫЪрВММВВ ЛМЪВ„рЛрУ‚‡МЛВ, ‡ ФУ Н‡НУИ – ‚МВ¯МВВ.
ирЛПВр 1. З˚˜ЛТОЛЪ¸ ФОУ˘‡‰¸ У·О‡ТЪЛ D , У„р‡МЛ˜ВММУИ НрЛ- ‚˚ПЛ y =x , x +y = 6 , y = 2 , y = 0 Ò ÔÓÏÓ˘¸˛ ‰‚ÓÈÌÓ„Ó ËÌÚ„ð‡Î‡ (ðËÒ. 1.1.8).
ê¯ÂÌËÂ. кВ¯ЛП Б‡‰‡˜Ы ‰‚ЫПfl ТФУТУ·‡ПЛ.
иВр‚˚И ТФУТУ·. ê‡ÁÓ·¸ÂÏ Ó·Î‡ÒÚ¸ D ̇ ÚðË Ó·Î‡ÒÚË D1 , D2 Ë D3 , Ôðӂ‰fl ÔðflÏ˚ x = 2 Ë x = 4 (ðËÒ. 1.1.8).
y
|
2 |
|
y =x |
|
|
|
y = 2 |
|
|
|
|
|
x +y = 6 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
D2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
|
|
D1 |
|
|
D3 |
|
|
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
4 |
6 |
||||||||||||||||
|
|
|
|
|
|
êËÒ. 1.1.8 |
|
|
|
|
|
|
|
|||||||||
íÓ„‰‡ |
ЛТНУП‡fl ФОУ˘‡‰¸ |
SD =SD1 +SD2 +SD3 , „‰Â |
SD1 = ∫∫dxdy, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
SD2 = ∫∫dxdy , SD3 = ∫∫dxdy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
D2 |
D3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
З˚˜ЛТОЛП Н‡К‰˚И ЛБ ЛМЪВ„р‡ОУ‚, ‚˚ФУОМflfl ‚МЫЪрВММВВ ЛМЪВ„- рЛрУ‚‡МЛВ ФУ ФВрВПВММУИ y , ‡ ‚МВ¯МВВ – ФУ ФВрВПВММУИ x . íÓ„‰‡ ÔÓÎÛ˜ËÏ:
SD1 = ∫∫dxdy = ∫2 dx∫x dy .
D1 |
0 0 |
x
á‰ÂÒ¸ I1 внутр = ∫dy =y x0 =x
0
éÍÓ̘‡ÚÂθÌÓ ÔÓÎÛ˜ËÏ:
13
SD1 = ∫2 xdx = x2 |
|
2 |
= |
22 |
= 2 . |
|
|
||||||
0 |
2 |
|
0 |
|
2 |
|
|
|
|
|
|||
б‡ПВЪЛП, ˜ЪУ ‰Оfl М‡ıУК‰ВМЛfl ФрВ‰ВОУ‚ ‚МЫЪрВММВ„У ЛМЪВ„рЛрУ- ‚‡МЛfl ФУ ФВрВПВММУИ y ÒΉÛÂÚ ˜ÂðÂÁ ӷ·ÒÚ¸ D1 ÔðÓ‚ÂÒÚË ÔðflÏÛ˛, Ô‡ð‡ÎÎÂθÌÛ˛ ÓÒË Oy Л ФУТПУЪрВЪ¸, ФрЛ Н‡НУП БМ‡˜ВМЛЛ y Ó̇ ‚ıÓ‰ËÚ ‚ ӷ·ÒÚ¸ D1 Ë ÔðË Í‡ÍÓÏ Á̇˜ÂÌËË y Ó̇ ËÁ ӷ·ÒÚË D1 ‚˚ıУ‰ЛЪ. щЪУ Л ·Ы‰ЫЪ ФрВ‰ВО˚ ЛМЪВ„рЛрУ‚‡МЛfl. Д ЛПВММУ: ‚ıУ- ‰ЛП ‚ У·О‡ТЪ¸ D1 ÔðË y = 0 (МЛКМЛИ ФрВ‰ВО ЛМЪВ„рЛрУ‚‡МЛfl), ‡
‚˚ıÓ‰ËÏ ËÁ ӷ·ÒÚË ÔðË y =x |
(˜ВрВБ ФрflПЫ˛, Ыр‡‚МВМЛfl НУЪУрУИ |
|||||||||||||||||||
y =x ; ˝ÚÓ ‚ÂðıÌËÈ Ôð‰ÂÎ ËÌÚ„ðËðÓ‚‡ÌËfl ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ). |
|
|||||||||||||||||||
ëÓ‚Âð¯ÂÌÌÓ ‡Ì‡Îӄ˘ÌÓ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
SD2 = ∫∫dxdy = ∫4 dx∫2 dy, |
|
I2 внутр = ∫2 dy =y |
|
02 = 2 ; |
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
D2 |
2 |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
SD2 = ∫4 2dx = 2∫4 dx = 2 x |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= 2(4 − 2) = 4 . |
|
|
|
|
|
|
|
|
|||||||||||
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
SD3 = ∫∫dxdy = ∫6 dx |
6∫−xdy , |
I3 внутр = |
6∫−xdy =y |
|
06−x = 6 −x ; |
|
|
|||||||||||||
|
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||
D3 |
4 |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
6 |
|
|
x2 |
|
|
6 |
|
|
|
36 |
|
16 |
|
|
||||||
|
|
|
|
|
|
|||||||||||||||
SD3 = ∫(6 −x)dx = |
6x − |
|
2 |
|
|
= |
|
36 − |
2 |
− 24 − |
=18 |
−16 |
= 2 . |
|||||||
4 |
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
= 2 + 4 + 2 =8 . |
|
|
|
|||||||||||
é˜Â‚ˉÌÓ, ˜ÚÓ SD =SD +SD |
+SD |
|
|
|
||||||||||||||||
|
|
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
àÚ‡Í, |
|
|
|
|
|
|
|
|
SD =8. |
|
|
|
|
|
|
|
|
|||
ЗЪУрУИ ТФУТУ·. З˚·Лр‡fl ‚МЫЪрВММВВ ЛМЪВ„рЛрУ‚‡МЛВ ФУ ФВрВПВММУИ x , ‡ ‚МВ¯МВВ ФУ ФВрВПВММУИ y , ПУКВП Б‡ФЛТ‡Ъ¸ ЛТНУПЫ˛ ФОУ˘‡‰¸ Ъ‡Н:
2 6−y
SD = ∫∫dxdy = ∫dy ∫ dx .
D 0 y
б‡ПВЪЛП, ˜ЪУ ФрЛ М‡ıУК‰ВМЛЛ ФрВ‰ВОУ‚ ‚МЫЪрВММВ„У ЛМЪВ„рЛрУ- ‚‡МЛfl (ФУ ФВрВПВММУИ x ), П˚ П˚ТОВММУ ФрУ‚В‰ВП ФрflПЫ˛, Ф‡р‡О- ОВО¸МЫ˛ УТЛ Ox . é̇ ‚ıÓ‰ËÚ ‚ ӷ·ÒÚ¸ D ÔðË x =y , ‡ ‚˚ıУ‰ЛЪ – ˜ВрВБ ФрflПЫ˛, Ыр‡‚МВМЛВ НУЪУрУИ x +y = 6 , Ú.Â. ÔðË x = 6 −y . б‡- НУМ˜ЛП ‚˚˜ЛТОВМЛВ:
14

6−y |
|
|
y6−y = (6 −y) −y = 6 − 2y ; |
||||
Iвнутр = ∫ dx =x |
|
||||||
|
|||||||
|
|||||||
y |
|
|
|
|
|
|
|
SD = ∫2 (6 − 2y)dy = 6y − 2 |
y2 |
|
|
2 =12 − 4 =8, |
|||
|
|||||||
0 |
|
|
|
2 |
|
|
0 |
|
|
|
|
||||
Ъ.В. Н‡Н Л ФрЛ ФВр‚УП ТФУТУ·В рВ¯ВМЛfl, П˚ ФУОЫ˜ЛОЛ, ˜ЪУ SD =8. |
|||||||
ирЛПВр 2. З˚˜ЛТОЛЪ¸: |
I = ∫∫(x +y2 )dxdy , |
||||||
|
|||||||
|
D |
|
|
|
|
||
„‰Â ӷ·ÒÚ¸ D Ó„ð‡Ì˘Â̇ ÔðflÏ˚ÏË |
y = 0 , y =x , x +y = 4 (ðËÒ. |
||||||
1.1.9). |
|
|
|
|
|
|
|
y
|
y =x |
|
x +y = 4 |
|
||||
|
|
|
|
|
|
|||
|
|
D1 |
|
|
D2 |
|
|
|
0 |
|
|
|
|
|
|
|
x |
1 2 |
3 4 |
|||||||
|
êËÒ. 1.1.9 |
|
|
|||||
ê¯ÂÌËÂ. кВ¯ЛП ФрЛПВ𠉂ЫПfl ТФУТУ·‡ПЛ.
иВр‚˚И ТФУТУ·. З˚ФУОМЛП ‚МЫЪрВММВВ ЛМЪВ„рЛрУ‚‡МЛВ ФУ ФВрВПВММУИ x , ‡ ‚̯Ì – ÔÓ y , ÚÓ„‰‡ ÔÓÎÛ˜ËÏ:
|
|
|
|
|
|
|
2 |
|
|
4−y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I = ∫dy |
∫ (x +y2 )dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З˚˜ЛТОЛП ‚МЫЪрВММЛИ ЛМЪВ„р‡О: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
4−y |
|
|
|
|
x2 |
|
2 |
|
4−y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Iвнутр = ∫ |
(x +y |
2 |
|
|
+xy |
|
|
= −2y |
3 |
+ 4y |
2 |
− 4y +8 . |
|
|
||||||||||||||
|
)dx = |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
иУ‰ТЪ‡‚Оflfl М‡И‰ВММУВ БМ‡˜ВМЛВ ‚ ‚˚р‡КВМЛВ ‰Оfl I , ÔÓÎÛ˜ËÏ: |
|
|
||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
3 |
|
2 |
|
|
|
|
|
|
y4 |
|
4y |
3 |
|
2 |
|
|
2 |
|
32 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
I = ∫∫(x +y |
|
)dxdy |
= ∫ −2y |
|
+ 4y |
|
− 4y + |
8 dy |
= |
− |
|
|
+ |
|
|
|
− 2y |
|
+8y |
|
|
= |
|
|||||
|
|
|
2 |
3 |
|
|
|
|
3 |
|||||||||||||||||||
D |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
.
ЗЪУрУИ ТФУТУ·. ЗМЫЪрВММВВ ЛМЪВ„рЛрУ‚‡МЛВ ‚˚ФУОМЛП ФУ ФВрВПВММУИ y , ‡ ‚̯Ì – ÔÓ x . б‡ПВЪЛП, ˜ЪУ ФрЛ ˝ЪУП У·О‡ТЪ¸ D Ï˚ ‰ÓÎÊÌ˚ ð‡Á·ËÚ¸ ̇ ‰‚ ӷ·ÒÚË D1 Ë D2 (Í‡Í Û͇Á‡ÌÓ Ì‡ ðËÒ.
15
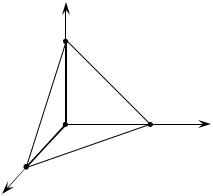
1.1.9); ТОВ‰У‚‡ЪВО¸МУ, ‰‚УИМУИ ЛМЪВ„р‡О ‚˚р‡БЛЪТfl ‚ ‚Л‰В ТЫПП˚
Ú‡ÍËı ‰‚Ûı ÔÓ‚ÚÓðÌ˚ı ËÌÚ„ð‡ÎÓ‚:
I = ∫2 dx∫x (x +y2 )dy + ∫4 dx4∫−x (x +y2 )dy =I1 +I2 .
0 |
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
+ y |
3 |
|
|
|
x |
|
=x |
2 + x |
3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
I1 внутр = ∫(x +y2 )dy = xy |
|
|
|
|
|
|
|
; |
|
|
|
|||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
0 |
|
|
|
|
|
|
3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
2 |
|
+ |
x3 |
|
|
x3 |
y4 |
|
|
2 |
= |
8 |
+ |
4 |
= |
4 . |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
I1 = ∫ |
x |
|
|
3 |
dx = |
3 |
+ |
12 |
|
|
|
|
3 |
3 |
|
|
|
|||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
4−x |
|
|
|
|
|
|
|
|
|
|
|
|
4−x |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
64 |
|
|
+3x2 − x |
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
I2 внутр = |
|
∫ (x +y2 )dy = |
xy + y |
|
|
|
|
|
= |
|
|
−12x |
|
; |
||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
0 |
|
|
|
|
3 |
|
|
3 |
|
|||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
64 |
|
|
|
2 |
|
|
x3 |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
I1 = ∫2 |
3 |
|
−12x +3x |
|
|
− |
|
3 dx = |
3 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
àÚ‡Í, ÓÍÓ̘‡ÚÂθÌÓ ÔÓÎÛ˜ËÏ: I =I1 +I2 = 4 + |
20 |
= 32 . |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
ирЛПВр 3. З˚˜ЛТОЛЪ¸ У·˙ВП |
|
Ú·, |
|
|
|
Ó„ð‡Ì˘ÂÌÌÓ„Ó |
ФОУТНУТЪ¸˛ |
|||||||||||||||||||||||||||||||
x +y +z =1 Л НУУр‰ЛМ‡ЪМ˚ПЛ ФОУТНУТЪflПЛ x = 0 , y = 0 , z = 0. |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x +y =1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
êËÒ. 1.1.10
ê¯ÂÌËÂ. ирЛМЛП‡fl ‚У ‚МЛП‡МЛВ „ВУПВЪрЛ˜ВТНЛИ ТП˚ТО ‰‚УИ-
МУ„У ЛМЪВ„р‡О‡, П˚ ПУКВП М‡ФЛТ‡Ъ¸, ˜ЪУ vT = ∫∫zdxdy.
D
á‰ÂÒ¸ D – ÚðÂÛ„ÓθÌËÍ, ÎÂʇ˘ËÈ ‚ ÓÒÌÓ‚‡ÌËË ÔËð‡Ïˉ˚, ‡ z = =1−x −y , Ú.Â.
16
vT = ∫∫(1−x −y)dxdy = ∫1 dx1−∫x (1−x −y)dy .
D |
0 |
0 |
ЗМЫЪрВММЛИ ЛМЪВ„р‡О:
1−x |
|
|
|
|
|
|
− y |
2 |
|
|
1−x |
|
|
|
(1−x) |
2 |
|
|
|
(1−x) |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Iвнутр = ∫ (1−x −y)dy = |
(1 |
−x) y |
|
|
|
= (1−x)2 − |
|
|
|
= |
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ëΉӂ‡ÚÂθÌÓ, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(1−x) |
2 |
|
1 |
1 |
|
|
|
|
|
|
1 |
|
+ x |
3 |
|
|
1 |
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
vT = ∫ |
|
dx = |
∫ |
(1− 2x +x2 )dx = |
x −x2 |
|
|
|
|
|
= |
, |
|
|||||||||||||
2 |
|
2 |
2 |
|
|
6 |
|
|||||||||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
3 |
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ъ.В. ЛТНУП˚И У·˙ВП ЪВО‡ T ð‡‚ÂÌ vT = 16 .
á‡Ï˜‡ÌËÂ. б‡ПВЪЛП, ˜ЪУ ЛТНУП˚И У·˙ВП П˚ ПУ„ОЛ ·˚ М‡ИЪЛ, ФУО¸БЫflТ¸ БМ‡МЛflПЛ, ФУОЫ˜ВММ˚ПЛ ‚ ТрВ‰МВИ ¯НУОВ. СВИТЪ‚ЛЪВО¸- МУ, ЪВОУ T ВТЪ¸ МВ ˜ЪУ ЛМУВ, Н‡Н ФЛр‡ПЛ‰‡, ФОУ˘‡‰¸ УТМУ‚‡МЛfl НУЪУрУИ ВТЪ¸ ФрflПУЫ„УО¸М˚И ЪрВЫ„УО¸МЛН AOB , Ôð˘ÂÏ
S AOB = 12 OA OB = 12 1 1 = 12 . Ç˚ÒÓÚ‡ ÔËð‡Ïˉ˚ h =OC =1.
vпир = 13Sосн h , Ú.Â.
vпир = 13 12 1 = 16 .
5.З˚˜ЛТОВМЛВ ФОУ˘‡‰Л НрЛ‚УИ ФУ‚ВрıМУТЪЛ Т ФУПУ˘¸˛ ‰‚УИМУ„У ЛМЪВ„р‡О‡.
к‡ТТПУЪрЛП ФУ‚ВрıМУТЪ¸, Б‡‰‡ММЫ˛ Ыр‡‚МВМЛВП F(x,y,z) = 0 . СУФЫТЪЛП, ˜ЪУ ЩЫМНˆЛfl F(x,y,z) МВФрВр˚‚М‡ Л ЛПВВЪ МВФрВр˚‚- М˚В ˜‡ТЪМ˚В ФрУЛБ‚У‰М˚В Fx′, Fy′, Fz′. СУФЫТЪЛП, ˜ЪУ ‚ТВ ЪрЛ ˜‡ТЪ-
М˚В ФрУЛБ‚У‰М˚В МВ У·р‡˘‡˛ЪТfl ‚ МУО¸ МЛ ‚ У‰МУИ ЪУ˜НВ ФУ‚ВрıМУТЪЛ S , Ú.Â. ÔÓ‚ÂðıÌÓÒÚ¸ S ‚ Н‡К‰УИ ЪУ˜НВ ЛПВВЪ Н‡Т‡ЪВО¸МЫ˛ ФОУТНУТЪ¸. е˚ ЫТЪ‡МУ‚ЛОЛ р‡МВВ, ˜ЪУ ФрЛ Ъ‡НЛı ФрВ‰ФУОУКВМЛflı ‚
͇ʉÓÈ ÚӘ͠M ФУ‚ВрıМУТЪЛ S ÒÛ˘ÂÒÚ‚ÛÂÚ ÌÓðχθ Í ÔÓ‚ÂðıÌÓ- uur
ÒÚË N , Ôð˘ÂÏ
uur |
|
∂F(x,y,z) |
|
|
r |
|
∂F(x,y,z) |
|
|
r |
∂F(x,y,z) |
|
|
ur |
|
|
|
|
|
|
|
||||||||
N |
= |
|
|
|
i |
+ |
|
|
|
j + |
|
|
|
k . |
∂x |
|
|
∂y |
|
|
∂z |
||||||||
|
|
|
M |
|
|
|
M |
|
|
|
M |
|||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
17

ur
N
ν |
μ |
z |
|
M |
|
λ |
|
S
y
0
D
x
êËÒ. 1.1.11
СУФЫТЪЛП, ‚ ˜‡ТЪМУТЪЛ, ˜ЪУ ФУ‚ВрıМУТЪ¸ S z = f(x,y) . й˜В‚Л‰МУ, ˜ЪУ П˚ ПУКВП Т˜ЛЪ‡Ъ¸
F(x,y,z) =z − f(x,y) ,
ФрЛ˜ВП, ˜‡ТЪМ˚В ФрУЛБ‚У‰М˚В
∂F = −∂f(x,y) , ∂F = −∂f(x,y) , ∂x ∂x ∂y ∂y
Б‡‰‡М‡ Ыр‡‚МВМЛВП
∂∂Fz =1
МВФрВр˚‚М˚ ‚ ТЛОЫ Т‰ВО‡ММ˚ı ‚˚¯В ФрВ‰ФУОУКВМЛИ. й·УБМ‡˜ЛП
|
∂f(x,y) |
= p(x,y) , |
∂f(x,y) |
=q(x,y) . |
|
|
∂x |
|
|
||
|
|
|
∂y |
||
нУ„‰‡ flТМУ, ˜ЪУ МУрП‡О¸ Н ФУ‚ВрıМУТЪЛ ‚ О˛·УИ ЪУ˜НВ M ·Û‰ÂÚ |
|||||
ËÏÂÚ¸ ÍÓÓð‰Ë̇Ú˚: uur |
|
uur |
|||
|
N |
=N (−p(x,y), −q(x,y),1). |
|||
Ц‰ЛМЛ˜М˚И ‚ВНЪУр МУрП‡ОЛ Н ФУ‚ВрıМУТЪЛ, ТОВ‰У‚‡ЪВО¸МУ, ЛПВ-
ÂÚ ‚ˉ: |
|
|
r |
ur |
|
|
uur0 |
|
|
||
|
= |
−p(x,y) i −q(x,y) j +k |
|
||
|
N |
|
|
, |
|
|
± p2 (x,y) +q2 (x,y) |
+1 |
|||
r |
r ur |
|
|
||
|
|
|
|
||
„‰Â i , |
j , k – УрЪ˚ ТЛТЪВП˚ НУУр‰ЛМ‡Ъ (рЛТ. 1.1.11). |
||||
д‡Н ЛБ‚ВТЪМУ, НУУр‰ЛМ‡Ъ˚ В‰ЛМЛ˜МУ„У ‚ВНЪУр‡ ТУ‚Ф‡‰‡˛Ъ Т М‡-
Фр‡‚Оfl˛˘ЛПЛ НУТЛМЫТ‡ПЛ ‰‡ММУ„У ‚ВНЪУр‡. й·УБМ‡˜ЛП ˜ВрВБ λ , μ ur
Ë ν Û„Î˚ ÌÓðχÎË N ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ Ò ÍÓÓð‰Ë̇ÚÌ˚ÏË ÓÒflÏË Ox , Oy, Oz . áÌ‡Í ± ‚ БМ‡ПВМ‡ЪВОВ ФУТОВ‰МВИ ЩУрПЫО˚ УБМ‡˜‡ВЪ, ˜ЪУ П˚ ПУКВП ‚˚·р‡Ъ¸ М‡ МУрП‡ОЛ ‰‚‡ ‚Б‡ЛПМУ ФрУЪЛ‚УФУОУКМ˚ı М‡-
18
Фр‡‚ОВМЛfl, Ъ.В. ‰Оfl М‡Фр‡‚Оfl˛˘Лı НУТЛМЫТУ‚ МУрП‡ОЛ ФУОЫ˜ЛП
Ъ‡НЛВ ЩУрПЫО˚: |
−p(x,y) |
|
|
||||
cos λ = |
|
|
; |
||||
± |
p2 (x,y) +q2 (x,y) +1 |
||||||
cos μ = |
|
−q(x,y) |
|
; |
|||
± |
p2 (x,y) +q2 (x,y) +1 |
|
|||||
cosν = |
|
|
|
1 |
. |
||
± |
p2 (x,y) +q2 (x,y) +1 |
||||||
б‡ЩЛНТЛрЫВП М‡ МУрП‡ОЛ ЪУ М‡Фр‡‚ОВМЛВ, НУЪУрУВ У·р‡БЫВЪ УТЪ- р˚И Ы„УО Т УТ¸˛ Oz , Ъ.В. ‚˚·ВрВП ‚ ЩУрПЫО‡ı ‰Оfl М‡Фр‡‚Оfl˛˘Лı НУТЛМЫТУ‚ Ъ‡НУИ БМ‡Н ФВрВ‰ НУрМВП, ˜ЪУ·˚ ·˚ОУ cosν > 0 .
аЪ‡Н, М‡Фр‡‚Оfl˛˘ЛВ НУТЛМЫТ˚ ‰Оfl МУрП‡ОЛ, У·р‡БЫ˛˘ВИ УТЪ- р˚И Ы„УО Т УТ¸˛ Oz , Ú‡ÍÓ‚˚:
cos λ = |
−p(x,y) |
|
; |
cos μ = |
|
−q(x,y) |
; |
|
p2 (x,y) +q2 (x,y) +1 |
p2 (x,y) +q2 (x,y) +1 |
|||||||
|
cosν = |
|
|
|
1 |
|
. |
|
|
|
p2 (x,y) +q2 (x,y) +1 |
|
|||||
СОfl МУрП‡ОЛ, ЛПВ˛˘ВИ ФрУЪЛ‚УФУОУКМУВ М‡Фр‡‚ОВМЛВ, ФУОЫ˜ЛП
ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ: |
|
|
|
|
|
||
cos λ = |
|
p(x,y) |
|
; cos μ = |
|
q(x,y) |
|
|
|
|
|
; |
|||
|
p2 (x,y) +q2 (x,y) +1 |
p2 (x,y) +q2 (x,y) +1 |
|||||
|
|
cosν = |
|
−1 |
|
. |
|
|
|
p2 (x,y) +q2 (x,y) +1 |
|||||
к‡ТТПУЪрЛП ЪВФВр¸ ФУ‚ВрıМУТЪ¸ S , р‡ТФУОУКВММЫ˛ М‡‰ ФрУТЪУИ |
|||||||
ӷ·ÒÚ¸˛ D , |
ÎÂʇ˘ÂÈ ‚ |
ФОУТНУТЪЛ xOy |
(ðËÒ. 1.1.12). ê‡ÁÓ·¸ÂÏ |
||||
ӷ·ÒÚ¸ D ТВЪ¸˛ ФрУТЪ˚ı ОЛМЛИ М‡ fl˜ВИНЛ D1 , D2 , ..., Dn Ò ÔÎÓ- ˘‡‰flÏË F1 , F2 , ..., Fn ; λ – ð‡Ì„ ‰ðÓ·ÎÂÌËfl D .
к‡ТТПУЪрЛП ˆЛОЛМ‰рЛ˜ВТНЛВ ФУ‚ВрıМУТЪЛ, У·р‡БЫ˛˘ЛВ НУЪУр˚ı Ф‡р‡ООВО¸М˚ УТЛ Oz , ‡ М‡Фр‡‚Оfl˛˘ЛПЛ ТОЫКЛЪ ‰рУ·fl˘‡fl ТВЪ¸ ОЛМЛИ У·О‡ТЪЛ D . щЪЛ ˆЛОЛМ‰рЛ˜ВТНЛВ ФУ‚ВрıМУТЪЛ ФВрВМУТflЪ ‰рУ·ОВМЛВ ЛБ У·О‡ТЪЛ D ̇ ÔÓ‚ÂðıÌÓÒÚ¸ S , НУЪУр‡fl р‡Б·Л‚‡ВЪТfl Ъ‡НЛП У·р‡БУП М‡ fl˜ВИНЛ S1 , S2 , ..., Sn . Ç˚·ÂðÂÏ ‚ ͇ʉÓÈ fl˜ÂÈÍ Sk ФрУЛБ‚УО¸МЫ˛ ЪУ˜НЫ Mk (xk ,yk ,zk ) Ë Ôðӂ‰ÂÏ ˜ÂðÂÁ Ì ͇҇- ÚÂθÌÛ˛ ÔÎÓ˘‡‰ÍÛ Tk ‰У ФВрВТВ˜ВМЛfl Т ‚˚¯ВМ‡Б‚‡ММ˚ПЛ ˆЛОЛМ‰-
19

рЛ˜ВТНЛПЛ ФУ‚ВрıМУТЪflПЛ. й·УБМ‡˜ЛП ФОУ˘‡‰¸ Н‡Т‡ЪВО¸МУИ ФОУ- ˘‡‰НЛ Tk ˜ÂðÂÁ Sk .
z |
Tk |
Mk (xk ,yk ,zk ) |
|
Sk |
|||
|
S |
0 |
y |
|
Dk |
|
|
|
,yk ) |
|
D |
(xk |
|
|
|
|
x |
|
|
êËÒ. 1.1.12 |
|
|
ÖÒÎË ÒÛ˘ÂÒÚ‚ÛÂÚ ÍÓ̘Ì˚È Ôð‰ÂÎ |
|
|
|
n |
|
S = lim |
∑ Sk , |
|
n→∞ |
k=1 |
|
λ→0 |
|
|
МВ Б‡‚ЛТfl˘ЛИ МЛ УЪ ТФУТУ·‡ ‰рУ·ОВМЛfl, МЛ УЪ ‚˚·Ур‡ ЪУ˜ВН Mk М‡ ФУ‚ВрıМУТЪЛ S , ЪУ УМ М‡Б˚‚‡ВЪТfl ФОУ˘‡‰¸˛ ФУ‚ВрıМУТЪЛ S , р‡Т- ФУОУКВММУИ М‡‰ У·О‡ТЪ¸˛ D , ‡ ҇χ ÔÓ‚ÂðıÌÓÒÚ¸ ‚ ˝ÚÓÏ ÒÎÛ˜‡Â ̇- Á˚‚‡ÂÚÒfl Н‚‡‰рЛрЫВПУИ.
z
|
ur |
νk |
N |
y |
|
0 |
Tk |
Dk
x
ϕk
êËÒ. 1.1.13
20
