2.4. Метод касательных

Рассмотрим алгоритм построения итерационной последовательности метода касательных, используя геометрический язык. Построим график функции f(x) на [a, b]. И пусть эта функция имеет на данном отрезке единственный корень.

Возьмемx₀ [a, b] и построим касательную к графику функции в точке x₀. Найдем точку пересечения касательной с Ox и обозначим ее через x₁. Затем построим касательную в точке x₁ и обозначим точку пересечения ее с осью Ox через x₂. Продолжая этот процесс, получим итерационную последовательность.

Не трудно проверить, что члены итерационной последовательности получаются по формуле: x_n+1=x_n-

В результате получим итерационный метод, который называется методом касательных. Сформулируем достаточные условия сходимости метода касательных:

Теорема 6. Пусть:

1. f(x)

2. f(a)f(b)<0

3. f^’(x) и f^’’(x) знакопостоянны на [a, b]

4. итерационная последовательность имеет вид:

x_n+1=x_n-, n=0,1,2,..

x₀=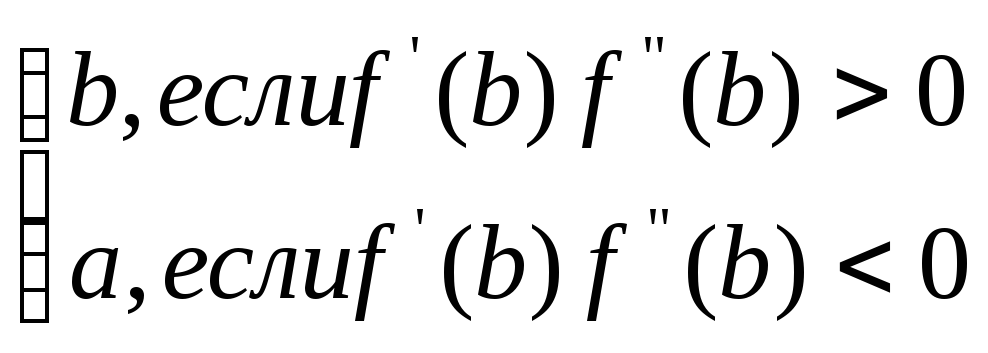

Тогда, , гдеX_c- единственный корень уравнения (1) на [a, b].

Доказательство: Существование и единственность x_c уравнения (1) следует из условия (2) и знакопостоянства производной на [a, b].

Докажем, что построенная итерационная последовательность сходится к x_c. При выполнении условия теоремы возможны четыре случая:

1. монотонно убывающая последовательность, ограниченная снизу

2. монотонно возрастающая последовательность, ограниченная сверху

3. монотонно возрастающая последовательность, ограниченная сверху

4. монотонно убывающая последовательность, ограниченная снизу

Во всех четырех случаях последовательность сходится. Докажем, что она сходится к x_c. x_n+1=x_n-

limx_n+1=limx_n-, т.к. x_c-единственный корень уравнения.

2.5. Метод секущих

Рассмотрим график функции y=f(x) на отрезке [a, b] и пусть на [a, b] существует единственный корень уравнения (1).

Положим х₀=a, x₁=b. Соединим точки с абсциссами x₀ и x₁ секущей и обозначим через x₂ точку пересечения секущей с осью Ox. Выберем тот из отрезков [a, x₂] или [x₂,b] на концах которого, функция принимает значения разных знаков. Применим тот же прием, т.е. соединим точки с абсциссами x₀, x₂, находим точку пересечения с осью абсцисс и обозначим ее через x₃.В результате получим итерационную последовательность.

Достаточные условия сходимости метода секущих:

Теорема 7. Пусть:

1. f(x)

2. f(a)f(b)<0

3. f^’(x) и f^’’(x) знакопостоянны на [a, b]

4. {x_n} имеет вид:

x_n+1=x_n-, nN

х₁=x₀=

Тогда , гдеx_c- единственный корень уравнения (1) на [a, b].

Доказательство аналогично предыдущей теоремы.

Оценка погрешности методов.

Рассмотрим вопрос об оценке погрешности методов касательных и секущих. Докажем неравенство: |x_n-x_c|≤.

Т.к. f^’(x)- непрерывна и f^’(x)≠0, то такое m>0 существует. f(x_n)=f(x_n)-f(x_c)=|т. Лагранжа|=f^’(c)(x_n-x_c), |f(x_n)|=|f^’(c)||x_n-x_c|≥m|x_n-x_c|

2.6. Комбинированный метод секущих и касательных

Заключается в совместном применении метода хорд и касательных.

Теорема 8. Пусть:

1. f(x)

2. f(a)f(b)<0

3. f^’(x) и f^’’(x) знакопостоянны на [a, b]

4. итерационная последовательность построена по формулам:

x_2n=x_2n-2-, x_2n+1=x_2n-1-, n.

x₁=x₀=

Тогда, итерационная последовательность сходится к x_c, где x_c- корень уравнения (1) и причем единственный на [a, b].

Рассмотрим, как оценить погрешность комбинированного метода. При выполнении условий теоремы, приближения с четными и нечетными номерами лежат по разные стороны от искомого корня. Поэтому, для оценки погрешности данного метода можно воспользоваться неравенством:

|x_n+1-x_c|≤|x_n+1-x_n|, n

X

x_n x_c x_n+1

Если - требуемая точность и |x_n+1-x_n|≤, то в качестве искомого приближенного значения можно взять любое число из отрезка [a, b].