
- •Математика
- •Утверждено редакционно-издательским советом ВоГту Составитель: Абильдин а.А., канд.Техн.Наук, доцент
- •Введение
- •Тема 1. Векторы. Линейные операции над векторами.
- •§1.1. Действия над векторами.
- •3.Скалярное произведение
- •1.3.Линейная зависимость и независимость векторов
- •Тема 2. Матрицы и определители
- •1.Транспонирование матриц
- •2. Сложение
- •3.Умножение матрицы на скаляр
- •4.Умножение матриц
- •§2.2. Обратная матрица
- •Тема 3. Решение систем линейных уравнений
- •Тема 4. Произведение преобразований
- •Тема 5. Собственные векторы линейных преобразований
- •Тема 6. Комплексные числа
- •Контрольная работа № 1
- •Тема 8. Предел и непрерывность функций
- •Тема 9. Производная и дифференциал
- •Исследование функций
- •Тема 10. Приближенное решение уравнений
- •Контрольная работа №2
- •Литература
§2.2. Обратная матрица
Пусть А - квадратная матрица. Матрица B называется обратной для матрицы А, если произведение этих матриц равно единичной матрице, т.е. АB = BA=E.
Если определитель квадратной матрицы не равен нулю, то эта матрица имеет обратную и притом единственную.
Правило. Для вычисления обратной матрицы необходимо осуществить следующие операции:
Вычислить определитель
 исходной матрицы; если он не равен
нулю, то обратная матрица существует.
исходной матрицы; если он не равен
нулю, то обратная матрица существует.Вычислить алгебраические дополнения элементов исходной матрицы: А11, А12,..., Аn1,... Аnn .
Составить из алгебраических дополнений матрицу

Транспонируя полученную матрицу, получить присоединенную
 .
.Разделив присоединенную матрицу на определитель, получить обратную матрицу
 ,
,
Сделать проверку
 ∙
∙ =E
=E
Пример.
Вычислить обратную матрицу для
 .
.
Проводим расчеты по пунктам, описанным выше:
1.

2.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3.
 .
.
4.
 .
.
5.
 =-
=-
 .
.
Тема 3. Решение систем линейных уравнений
3.1. Метод обратной матрицы
Пример.
Решить систему уравнений:
 .
.
Запишем систему в матричном виде: вместо
 имеем
имеем
 ,
где
,
где
 ;
;
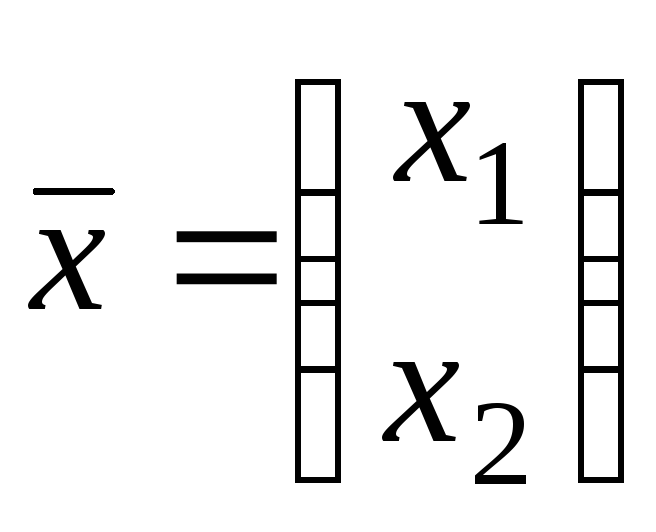 ;
;
 ,
то
,
то

Найдем обратную матрицу:
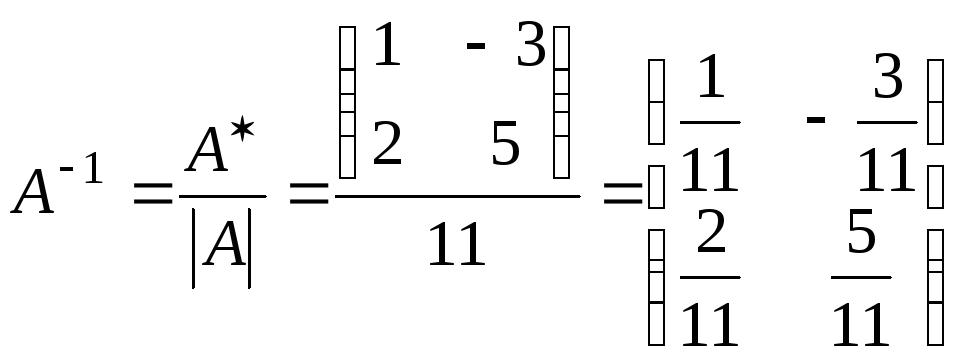 .
.
3. Вычисляем искомый вектор:
 ,
,
где
![]() ,
,
![]() .
.
Сделаем проверку, подставив полученный результат в данную систему:
![]() .
.
![]() .
.
3.2. Метод Гаусса
Рассмотрим систему m уравнений,связывающих n неизвестных
 (1)
(1)
Здесь aij (1≤i≤m , 1≤j≤m) коэффициенты; bj – cвободные члены. Если все коэффициенты и свободный член какого- то уравнения равны нулю , то вычеркиваем его из системы. Если коэффициенты при всех неизвестных равны нулю, а b≠0 , то система решений не имеет .
Условимся,что первым в системе (1) стоит уравнение, в котором коэффициент при первом неизвестном отличен от нуля (например а11≠0). Запишем систему (1) в виде матрицы опустив неизвестные и отделяя свободные члены вертикальной чертой
 (2)
(2)
Делим
все элементы первой строки на
![]()
 (3)
(3)
Затем из каждой 2-й,3-й,...,m-й строки матрицы (3) вычитаем почленно первую строку умноженной соответственно на a21,a31,..,am1 ; при этом результат вычитания получится в виде
 (4)
(4)
где
![]() =
=![]() -
-![]()
![]() ,...,
,...,![]() =b2
–
=b2
–
![]() .
.
Повторяя указанную операцию необходимое число раз,получим матрицу вида
 (5)
(5)
Полученной матрице соответствует система уравнений
 (6)
(6)
Пользуясь тем,что система имеет треугольный вид,ее можно решать последовательно, начиная с последнего уравнения.
Пример. Решить систему линейных уравнений методом Гаусса
 (7)
(7)
Матрица этой системы имеет вид
![]()
 (8)
(8)
Первую строку матрицы (8) умноженную на 2 и на 3 вычитаем из второй и третьей, соответственно
( (9)
(9)
Далее, к третьей строке матрицы (9) прибавив вторую, получим матрицу

соответствующей системе

Значит, решением системы (7) будет
![]()
![]() ,
,
![]() .
.
