
000000315551
.pdf
энергии — электромоторы, лампы, электропечи и т.д. — работают при низком напряжении, обычно в несколько сотен вольт, то на местных подстанциях вблизи потребителей принимаемое высокое напряжение понижается трансформаторами в соответствующее число раз.
Сформулируем теперь конкретно задачу расчета выходного напряжения генератора (электростанции). В нулевом приближении можно считать, что энергетические процессы в линии передачи переменного тока описываются выражениями (1-4), полученными для линии постоянного тока. Пусть имеется генератор с проектной мощностью Рг и линия передачи сопротивлением Rл, т.е. величины Rл и Pг заданы. Требуется определить выходное напряжение генератора, при котором относительная потеря мощности (напряжения) при передаче ее потребителю не превышала бы заданной величины (обычно до 10%).
Решение. По определению:
Pл= Pг
Но, с другой стороны, по закону Джоуля-Ленца:
P I 2 R |
|
|
Pг |
2 R |
, |
||||
|
|
|
|||||||
л |
л |
|
|
|
|
|
л |
||
|
|
|
|
Uг |
|
|
|
||
следовательно: |
|
|
|
|
|
|
|
|
|
|
P |
|
|
Pг |
|
2 R . |
|
|
|
|
|
|
|
|
|
||||
|
г |
|
|
|
л |
|
|
||
|
|
Uг |
|
|
|
||||
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
Uг |
Pг Rл |
. |
(5) |
||
|
|||||
|
|
|
|
||
Из этого выражения видно, что при заданных мощности генератора и сопротивлении линии потери в линии обратно пропорциональны квадрату напряжения генератора:
~ 12 ,
Uг
т.е., повысив напряжение, например, в 10 раз, мы получим уменьшение потерь в 100 раз.
Если энергия передается потребителю не непосредственно от электростанции, а от некоторого промежуточного распределителя, например, от районной подстанции в дальнее село, то расчет выходного напряжения подстанции Uг ведется не по мощности генератора Рг, а по мощности Рн, которую надо доставить потребителю при заданных потерях , так как отдельный потребитель берет через подстанцию лишь часть мощности генератора. В этом случае задача решается так. В формулу (5) вместо Рг подставляется величина Рн/(1 ), поскольку:

Рн=(1 )Рг.
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
Uг |
Pн Rл . |
(6) |
|||
(1 |
) |
|
|
||
|
|
|
|||
Отсюда видно, что потери , если они невелики, также примерно обратно пропорциональны квадрату напряжения Uг. Соотношение (6) можно использовать и для проектирования ЛЭП при заданной мощности потребителя Рн, максимально допустимом (по каким-либо причинам) напряжении Uг и допустимых потерях .
Из выражений (5) и (6) также следует, что потери в линии уменьшаются при уменьшении ее сопротивления Rл. А это означает, что потребителя (нагрузку) выгоднее подключать как можно ближе к генератору, или же строить электростанции по возможности ближе к потребителям.
3.1.2. Распределение напряжения в линии
Если всю линию разделить на множество равных небольших участков длиной x и измерить сопротивления пары проводов на каждом из них, то получатся величины Rx, вообще говоря, не равные друг другу, так как линия может быть составлена из проводов разной толщины и материала.
Определение. Предел отношения
lim |
Ri |
|
dR |
|
x |
dx |
|||
x 0 |
|
называется погонным сопротивлением линии. Вообще говоря, = (х), где х — координата вдоль линии. Если же=const по всей линии, то линия называется однородной.
Пусть однородная линия нагружена в конце на некоторое сопротивление Rн. Тогда легко показать, что напряжение между проводами линии
U(х) будет линейно уменьшаться от генератора к нагрузке (см. рис.3.1.3), т.е. U(х) будет иметь вид:
U(x)=Uг k x |
(7) |
где k — коэффициент, зависящий от сопротивлений линии и нагрузки. Величина U(х) называется напряжением в данном сечении линии.
Если в каком-либо промежуточном сечении линии к ней подключить еще дополнительную нагрузку Rн’, то характер распределения на-

пряжения примет вид ломаной, полностью лежащей под первоначальной прямой (см. рис.3.1.3 — пунктир). В реальной практике подключение слишком мощного потребителя где-нибудь в середине ЛЭП может привести к недопустимому уменьшению напряжения у потребителей на дальних участках линии.
3.1.3. Экспериментальная установка.
Экспериментальная модель ЛЭП представляет собой спаренный реохорд с двумя парами скользящих контактов, к которым могут подключаться вольтметр и нагрузка. Нагрузку можно подключить также и в конце линии (см. рис.3.1.4). В качестве нагрузок используются магазины сопротивлений. На вход линии пода-
Рис.3.1.4. Экспериментальная мо-
ется постоянное напряжение Uг от
дель линии электропередачи блока питания. Ток в цепи измеряется миллиамперметром.
Данную настольную линию можно считать моделью реальной ЛЭП, уменьшенной примерно в миллион раз, так как погонное сопротивление используемой в модели нихромовой проволоки примерно во столько же раз больше погонного сопротивления проводов реальной ЛЭП.
В экспериментальной части данной работы исследуется эффективность передачи электроэнергии при различных выходных напряжениях генератора, но при постоянной его мощности, т.е. осуществляется проверка соотношения (5) и его следствие:
|
1 |
U 2 |
|
||
|
|
г1 |
. |
(8) |
|
|
2 |
U 2 |
|
||
|
|
г2 |
|
||
3.1.4.Программа работы
1.Собрать цепь согласно рис.3.1.4, но пока без нагрузок. Включить вольтметр и генератор, выставив напряжение на его выходе от 3 до 5 В.
2.Определить общее сопротивление обоих проводов линии, измерив напряжение генератора и ток в линии, накоротко замкнутой на конце.
3.Подключить к концу линии нагрузку Rн1 1 2 Rл. Измерить ток I1 в линии. При невысоком напряжении генератора (например, при Uг=5 В) снять распределение напряжения U(х) по всей линии с интервалом в 10 см.
4.По известным сопротивлениям Rн1 и Rл и измеренным напряжению Uг1 и току I1 вычислить величины Рг, Рн1, Рл1, 1 и 1. Проверить соотношение (5).
5.Повысить напряжение генератора Uг до 15 В и вычислить ток I2, соответствующий мощности, которую отдавал генератор в предыдущем опыте (п.3 и п.4). Увеличивая сопротивление нагрузки и следя за показанием миллиамперметра, добиться установления в цепи именно такого тока. Снять новую зависимость U(х).
6.По известным величинам Rн2, Rл, Uг2 и I2 вычислить величины
Рн2, Рл2, 2 и 2. Вновь проверить соотношение (5). Проверить пропорцию
(8).
7. Изучить влияние промежуточной нагрузки Rн’ в линии на распределение напряжения в ней, и в частности — на уменьшение напряжения на потребителе в конце линии. Для этого подключить добавочную нагрузку сопротивлением Rн’ Rн2 в каком-либо внутреннем сечении линии, например, при х=40 см, и при напряжении источника Uг2 и сопротивлении на конце Rн2 снять зависимость U(х) вдоль всей линии (0 x l), где l
—длина линии.
Вкачестве результатов представляются все расчетные величины по п.п.4-6, а также все экспериментальные данные. Три зависимости U(х) оформляются в виде таблиц и графиков в одном масштабе и на общем листе. На каждом графике должны быть указаны величины I, Rн, а на по-
следнем — Rн’.
3.1.5.Контрольные вопросы и задания
1.Что такое относительная потеря мощности (напряжения) в линии? Как она связана с КПД?
2.Почему передавать электроэнергию на большие расстояния выгоднее при высоком напряжении?
3.Что такое погонное сопротивление линии?
4.Непосредственным расчетом доказать зависимость (7) для однородной линии и определить коэффициент k.
5.Изобразить эквивалентную схему и дать качественный вид графика U(х) для линии, нагруженной на конце и в середине сопротивлениями Rн и Rн’ соответственно, если: а) Rн=0, Rн’ 0; б) Rн 0, Rн’=0.
6.Генератор мощностью 5000 кВт передает энергию по двум медным проводам заводу, находящемуся на расстоянии 250 км. Допустимая потеря мощности в проводах 2%. Рассчитать диаметр проводов для случаев, когда энергия передается под напряжением 100 кВ и 10 кВ.
7.От подстанции с выходным напряжением 100 кВ требуется передать к нагрузке на расстояние 10 км мощность 5 МВт. Определить минимальный диаметр медного провода, чтобы потери напряжения в линии не превышали 1%.
8.Дом подключен к магистральной линии проводом, имеющим сопротивление 1 0м. Напряжение в магистрали 220В. Определить максимально допустимую мощность, потребляемую в доме, если напряжение на включаемых в сеть приборах не должно падать ниже 210В.
3.1.5. Литература
С.Г. Калашников. Электричество. М.: “Наука”, 1985. § 71.
3.2. Исследование цепи постоянного тока (Лабораторная работа №4)
Целью работы является освоение методов расчета сложных цепей постоянного тока и экспериментальная проверка уравнений Кирхгофа.

3.2.1.Методы расчета электрических цепей
3.2.1.1.Правила Кирхгофа
Правила Кирхгофа являются основными соотношениями, на которых базируются расчеты сложных электрических цепей. Пусть имеется разветвленная сеть проводов, в различных участках которой находятся источники ЭДС Ek и постоянные сопротивления Rk (см.
рис.3.2.1). Величины Ek и Rk заданы. Такая сеть называется цепью постоянного тока. Ставится задача: рассчитать токи в каждой ветви этой цепи2. Такую задачу удобно решать с помощью двух правил Кирхгофа.
Первое правило относится к узлам цепи и утверждает следующее: алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.
ik 0 . |
(1) |
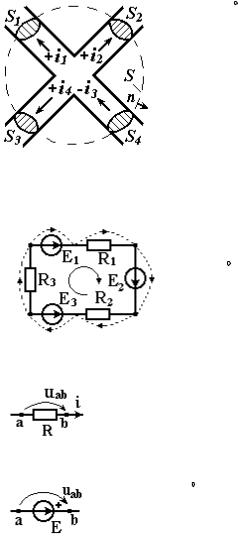
При этом входящим в узел токам условно приписывается один знак (обычно " "), а выходящим — другой (обычно "+"). Это правило означает то, что заряды в узле не накапливаются (сколько входит, столько и выходит), и следует из закона сохранения электрического заряда. Действительно, окружим узел произвольной замкнутой поверхностью S, обозначим сечения проводов этой поверхностью через Sk, а токи в них через ik (см. рис.3.2.2). Применим к поверхности S закон сохранения заряда:
dq
jdS .
S dt
Так как заряд q в узле, т.е. внутри поверхности S не меняется, то:
jdS 0 .
S
Но поскольку токи есть только в проводах, т.е. только в сечениях Sk, то получаем:
2 Ветвью или участком называется фрагмент цепи, соединяющий два узла и
содержащий элементы цепи (например, сопротивления и (или) источники ЭДС).
Узлом называется точка соединения трех или более ветвей цепи.
|
|
|
|
|
|
|
|
0 jdS |
jk dS ik |
, |
|||
|
S |
Sk |
|
|
|
|
|
т.е. соотношение (1). Применительно к узлу, |
|||||
|
показанному на рис.3.2.2, первое правило |
|||||
|
Кирхгофа примет вид (положительными будут |
|||||
|
токи, ориентированные в направлении нормали |
|||||
|
n): |
|
|
|
|
|
|
i1 + i2 i3 + i4 = 0. |
|
|
|||
|
Второе правило Кирхгофа относится к |
|||||
Рис.3.2.2. К выводу первого |
любому выделенному в цепи замкнутому кон- |
|||||
туру и утверждает следующее: алгебраическая |
||||||
правила Кирхгофа |
||||||
сумма напряжений на всех элементах произ- |
||||||
|
||||||
вольного замкнутого контура равна нулю: |
|
|
|
|
||
|
uk ( Rk ik Ek ) 0 . |
(2) |
||||
|
Это правило следует из основного свойства |
|||||
|
электростатического поля: |
|
|
|||
|
|
0 , |
|
|
|
|
|
Edl |
|
|
(3) |
||
|
L |
|
|
|
|
|
|
где L — произвольный замкнутый контур. |
|||||
|
Покажем справедливость (2). Рассмотрим ка- |
|||||
|
кой-либо контур цепи, |
изображенной на |
||||
Рис.3.2.3. К выводу второго |
рис.3.2.1, например внешний, |
и |
мысленно |
|||
правила Кирхгофа |
проведем замкнутую кривую L, |
показанную |
||||
на рис.3.2.3 штриховой линией. Если нет переменного магнитного поля, то вдоль этой кривой выполняется соотношение (3). Кон-
|
турный интеграл от поля Е вдоль этой кривой состоит из |
|
нескольких частей. Каждая часть — это интеграл от одно- |
|
го вывода элемента цепи до другого, и такой интеграл на- |
Рис.3.2.4. |
зывается напряжением, или падением напряжения на дан- |
Uab = Ri |
ном элементе (см. рис.3.2.4, рис.3.2.5). Следовательно: |
|
|
(uR |
|
|
Edl |
uE |
) 0 , |
||
L |
|
k |
|
k |
|
|
|
|
|
Рис.3.2.5.
Uab= E
где, по закону Ома:
uRk Rk ik —
падение напряжения на сопротивлении Rk замкнутого контура;
uEk Ek —
падение напряжения на источнике ЭДС.

Таким образом, получаем выражение (2). При записи (2) следует руководствоваться следующим правилом знаков3:
1) Если направление вычисления напряжения на сопротивлении Rk совпадает с направлением вычисления тока через него (см. рис.3.2.4), то падение напряжения на Rk записывается в (2) со знаком “+” (в противном случае — со знаком “ ”);
2) Если направление вычисления напряжения на источнике Ek противоположно стрелке ЭДС, то падение напряжения на нем записывается в (2) со знаком “+”. Если стрелка напряжения совпадает по направлению со стрелкой ЭДС, то падение напряжения на источнике записывается со знаком “ ” (см. рис.3.2.5).
Правила Кирхгофа (1) и (2) позволяют записать полную систему линейных алгебраических уравнений 1-го порядка, из которой можно однозначно определить токи во всех ветвях цепи. Практически последовательность составления таких уравнений следующая:
1.Задать произвольно направления вычисления токов ik во всех ветвях цепи4. Если в результате вычислений какой-либо ток окажется отрицательным, то это будет означать, что положительные заряды дрейфуют в направлении, противоположном поставленной стрелке.
2.Записать систему узловых уравнений (1), руководствуясь выбором знаков для входящих и выходящих токов. Если в цепи Y узлов, то независимых уравнений типа (1) будет Y-1. В этом несложно убедиться, сложив любые Y-1 разных узловых уравнений для произвольной электрической цепи. В результате сложения получится последнее неучтенное узловое уравнение. Таким образом, линейно независимыми являются любые уравнения типа (1) для Y-1 несовпадающих узлов.
3.Уравнения типа (2) должны учитывать все независимые контуры цепи, т.е. такие, которые нельзя образовать наложением всех остальных учтенных, друг на друга. Необходимое количество K контурных уравнений можно определить из условия:
K=B (Y 1),
где B — количество ветвей цепи, которое совпадает с количеством неизвестных токов ik. В качестве независимых удобно выбирать только все простые контуры, т.е. не содержащие в себе других контуров.
3 Направление вычисления напряжения на каждом элементе замкнутого
контура совпадает с направлением обхода контура.
4 Под направлением вычисления тока понимается направление нормали n к
сечению проводника (см. рис.3.2.2). Это направление принято обозначать на схемах стрелкой тока. Ток в проводнике положителен, если в направлении стрелки тока движутся положительные заряды.

4. Выбрать простые контуры и произвольным образом задать направление их обхода. Для каждого контура записать уравнение (2) с учетом правила знаков при вычислении напряжения на элементах.
Полученная неоднородная система алгебраических уравнений (если она составлена правильно) содержит B линейно независимых уравнений для B неизвестных токов и имеет единственное решение.
Пример. Вычислить токи через R1, R2 и R3 в цепи, показанной на рис.3.2.6, если номиналы всех элементов Rk и Ek этой цепи заданы.
Расставляем произвольно стрелки токов i1, i2 и i3 в ветвях цепи, как показано на рис.3.2.6. Так как независимый узел только один, то уравнений типа (1) будет одно:
i1 i2 i3=0.
Из трех возможных контуров I, II и III (см. рис.3.2.6) выберем два простых (I и II). Задаем в этих контурах произвольные направления обхода, например, по часовой стрелке, и записываем для
них уравнения типа (2) с учетом правила знаков:
i1 R1 +i2 R2 E1 E2 = 0,i2 R2+i3 R3 E3 +E2 = 0.
( Уравнение для контура III является зависимым, так как он образуется наложением контуров I и II.)
Таким образом, имеем систему трех уравнений для трех искомых токов. После решения системы, знаки полученных токов покажут, в каком направлении их следует считать положительными.
3.2.1.2. Метод узловых потенциалов
Для достаточно сложных цепей правила Кирхгофа приводят к слишком громоздким системам уравнений. В связи с этим были разработаны более эффективные методы расчета цепей, которые, хотя и базируются на правилах Кирхгофа, но требуют нахождения меньшего числа неизвестных, а значит содержат меньше уравнений. Один из таких методов
— метод узловых потенциалов. Если цепь содержит Y узлов, то этот метод приводит лишь к (Y 1) алгебраическим уравнениям, сколько дает лишь первое правило Кирхгофа.
За неизвестные в данном методе принимаются потенциалы узловk. Если потенциалы всех узлов известны, ток в любой ветви между двумя узлами "k" и "п" можно определить по закону Ома для участка цепи с ЭДС (см. рис.3.2.7):
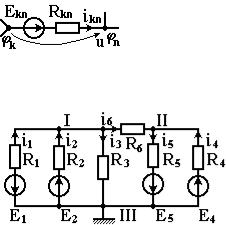
u = k n = iknRkn Ekn |
(4) |
Пусть цепь имеет Y узлов. В силу того, что потен- |
|
циал определен с точностью до аддитивной постоянной, один узел всегда можно заземлить и принять его потенциал равным нулю. Следовательно, остается Y 1 неизвестных величин k. Так, например, для схемы, показанной на рис.3.2.6, метод
узловых потенциалов приводит всего одному уравнению.
Рассмотрим алгоритм данного метода на примере более сложной цепи, показанной на рис.3.2.8. Она имеет три узла (I, II и III) и четыре независимых контура. Прямое использование правил Кирхгофа привело бы здесь к шести уравнениям относительно неизвестных токов в ветвях. Метод узловых по-
тенциалов приводит лишь к двум уравнениям. Заземлим, например, узел III, положив 3=0, и определим потенциалы узлов I и II, т.е. 1 и 2. Расставим произвольно стрелки токов в ветвях и запишем первое правило Кирхгофа для узлов I и II:
i1 i2 i3 i6 0 ; |
||||
|
i |
i |
i |
0 . |
|
4 |
6 |
5 |
|
Теперь выразим эти токи из закона Ома (4) с учетом правила знаков:
|
|
|
|
1 |
E1 ( 3 1 ) |
|||||
i1 |
|
|
||||||||
|
|
|
|
|||||||
|
|
|
R1 |
|
|
|
|
|||
|
|
|
|
1 |
|
|
E2 |
( 3 1 ) |
||
i2 |
|
|
|
|
|
|||||
|
R2 |
|
||||||||
|
|
|
|
|
|
|
|
|||
|
i3 |
1 |
|
0 |
( 1 3 ) , |
|||||
|
|
R |
|
|
||||||
|
|
|
|
|
3 |
|
|
|||
, i4 |
|
1 |
|
E4 ( 3 2 ) , |
||
|
|
|
||||
|
|
R4 |
||||
, i5 |
|
1 |
E5 ( 2 3 ) , |
|||
|
|
|||||
|
|
R5 |
||||
i6 |
|
1 |
01 ( 1 2 ) . |
|||
|
|
|||||
|
|
|
R6 |
|||
(5)
(6)
Подставим эти выражения для токов в (5) и учтем, что 3=0. После подстановки получим систему двух уравнений относительно неизвестных потенциалов 1 и 2:
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
E |
2 |
|
|
E |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
R2 |
|
|
R3 |
|
|
|
|
|
1 |
|
|
R6 |
|
|
|
R2 |
|
|
R1 |
|||||||||||||
R1 |
|
|
|
|
|
|
|
R6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
E |
4 |
|
|
|
E |
5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
R 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
R4 |
|
|
R5 |
|
|
R6 |
|
|
|
|
|
R4 |
|
|
|
R5 |
|||||||||||||
