
- •1. Введение.
- •2. Основные определения.
- •2.1 Различимость, изоморфизм и минимизация.
- •2.2 Проблемы тестирования.
- •2.3 Установочная последовательность.
- •2.4 Синхронизирующие последовательности.
- •3. Идентификация и верификация состояния.
- •3.2. Простые условные диагностические эксперименты.
- •3.3. Построение простого условного диагностического эксперимента.
- •3.4. Верификация состояния.
- •4. Тест На Соответствие.
- •4.1. Статусные Сообщения и Сброс.
- •4.2. Разделяющие Последовательности.
- •5. Вывод.
- •6. Список литературы
- •7.Приложение.
3.3. Построение простого условного диагностического эксперимента.
Первый алгоритм описывает образование разбиения и построение дерева. Второй алгоритм строит простой условный диагностический эксперимент, используя полученное дерево.
Дерево
T
имеет корень. Каждая вершина дерева
обозначена набором состояний, корень
подписан набором всех состояний, набор
внутренних вершин представляет собой
объединение обозначений его потомков.
Обозначение листьев образует разбиение
начальных состояний
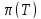 множества состояний автомата M.
Дерево считается завершенным, если
разбиение дискретно. Вдобавок, мы
связываем входную последовательность
p
с каждой внутренней вершиной. Каждое
ребро дерева обозначено выходным
символом. Далее используется обозначение
множества состояний автомата M.
Дерево считается завершенным, если
разбиение дискретно. Вдобавок, мы
связываем входную последовательность
p
с каждой внутренней вершиной. Каждое
ребро дерева обозначено выходным
символом. Далее используется обозначение
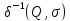 относительно множества Q
и последовательности
относительно множества Q
и последовательности
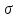 ,
его мы используем для обозначения
множества состояний
,
его мы используем для обозначения
множества состояний
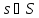 для которых,
для которых,
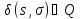 .
.
Допустимый
сигнал a
для блока Q
текущего разбиения
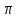 принадлежит одному из трех типов: 1) два
или более состояний Q
выдают разные выходные сигналы на a,
2) все состояния выдают одинаковые
выходные сигналы, но они переходят в
более, чем один блок
принадлежит одному из трех типов: 1) два
или более состояний Q
выдают разные выходные сигналы на a,
2) все состояния выдают одинаковые
выходные сигналы, но они переходят в
более, чем один блок
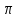 ,
3) ни одно из выше упомянутых, т.е. все
состояния выдают одинаковый выходной
сигнал и переходят в один блок
,
3) ни одно из выше упомянутых, т.е. все
состояния выдают одинаковый выходной
сигнал и переходят в один блок
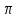 .
Определим представление
.
Определим представление
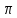 графом
графом
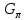 ,
это направленный граф с блоками
,
это направленный граф с блоками
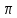 в качестве вершин и переходами между
блоками с одинаковым количеством
состояний. Переход
в качестве вершин и переходами между
блоками с одинаковым количеством
состояний. Переход
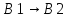 обозначается входным символом a
и выходным символом o,
если a
допустимый вход типа 3) для
обозначается входным символом a
и выходным символом o,
если a
допустимый вход типа 3) для
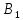 и образует биективное соответствие в
и образует биективное соответствие в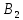 с выходом o.
с выходом o.
Алгоритм I:
Что нужно: Минимизированный автомат M.
Что получим: Готовое дерево ST, если M имеет простой условный диагностический эксперимент.
Метод:
1) Для начала обозначим дерево ST одной вершиной, корнем, обозначенным тривиальным текущим разбиением.
2)
Обозначим за R
набор блоков с наибольшей мощностью.
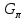 это граф, реализующий
это граф, реализующий
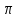 ,
а
,
а
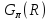 это подграф, образованный R.
Для каждого блока B
множества R,
u(B)
будет листом текущего дерева ST,
обозначенный как B.
Расширяем ST
тех пор, пока
это подграф, образованный R.
Для каждого блока B
множества R,
u(B)
будет листом текущего дерева ST,
обозначенный как B.
Расширяем ST
тех пор, пока
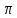 не станет дискретным.
не станет дискретным. 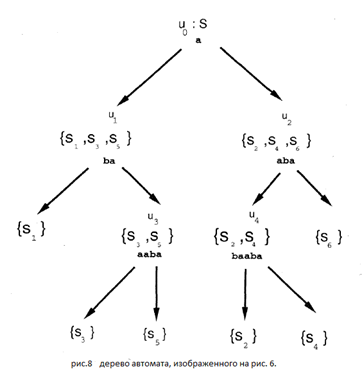
Случай 1: Если есть допустимый входной символ a для B, тогда связываем сигнал aс вершиной u(B). Каждое подмножество состояний B, которые выдают одинаковый выход, соединяется с u(B) как его лист и подписывается как совокупность этих состояний. Ребро подписано выходным сигналом.
Случай
2: Если же есть допустимый входной символ
a
типа 2) для B.
Пусть v
будет низшей вершиной ST,
чье обозначение содержит в себе множество
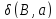 (v
это не лист). Если
(v
это не лист). Если
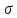 это последовательность, связанная с v.
Тогда последовательность, связанная с
вершиной u(B),
имеет вид a
это последовательность, связанная с v.
Тогда последовательность, связанная с
вершиной u(B),
имеет вид a .
Для каждого потомка v,
чье обозначение Q
пересекается с
.
Для каждого потомка v,
чье обозначение Q
пересекается с
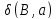 ,
присоединяем к u(B)
потомка и обозначаем его как
,
присоединяем к u(B)
потомка и обозначаем его как
 .
Ребро, инцидентное с u(B),
называется также как и смежное ребро к
v.
.
Ребро, инцидентное с u(B),
называется также как и смежное ребро к
v.
Случай
3: В противном случае, ищем путь в
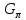 от
B
к C,
который попадает под случаи 1) и 2). Если
такой путь не существует, тогда прерываем
процесс и объявляем, что конечный автомат
не имеет простой условный диагностический
эксперимент. Иначе, обозначим за
от
B
к C,
который попадает под случаи 1) и 2). Если
такой путь не существует, тогда прерываем
процесс и объявляем, что конечный автомат
не имеет простой условный диагностический
эксперимент. Иначе, обозначим за
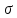 такой путь. К этому моменту u(C)
уже было определено и связана с
последовательностью
такой путь. К этому моменту u(C)
уже было определено и связана с
последовательностью
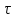 ,
полученной предыдущими шагами. Расширим
дерево как в случае 2) свяжем с u(B)
последовательность
,
полученной предыдущими шагами. Расширим
дерево как в случае 2) свяжем с u(B)
последовательность
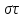 .
Для каждого потомка u(С),
чье обозначение Q
пересекается с
.
Для каждого потомка u(С),
чье обозначение Q
пересекается с
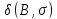 ,
присоединяем к u(B)
потомка с обозначением
,
присоединяем к u(B)
потомка с обозначением
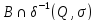 .
Ребро инцидентное с u(B)
называется так же, как и смежное ребро
к u(C).
.
Ребро инцидентное с u(B)
называется так же, как и смежное ребро
к u(C).
Пример:
Рассмотрим конечный автомат на рис.6.
Дерево для него показано на рис.8.
Единственный допустимый сигнал для S
это a,
который разделяет S
на два блока по 3 состояния в каждом. Оба
блока рассмотрены за следующую итерацию.
Блок с названием
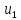 имеет допустимый сигнал b
типа 2), который переводит его в корень,
получает последовательность ba
и двух потомков. Блок
имеет допустимый сигнал b
типа 2), который переводит его в корень,
получает последовательность ba
и двух потомков. Блок
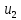 имеет только допустимый сигнал a
типа 3), и имеет путь длины один до графа
для
имеет только допустимый сигнал a
типа 3), и имеет путь длины один до графа
для
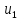 , таким образом,
, таким образом,
 имеет сигнал aba.
В следующей итерации рассматриваем
блоки
имеет сигнал aba.
В следующей итерации рассматриваем
блоки
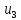 и
и
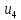 .
Оба входных сигнала типа допустимы для
.
Оба входных сигнала типа допустимы для
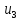 и имеют тип 2), выбираем a.
Тогда последовательность для
и имеют тип 2), выбираем a.
Тогда последовательность для
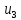 есть aaba.
Блок
есть aaba.
Блок
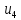 имеет оба допустимых сигнала типа 3), и
оба переводят
имеет оба допустимых сигнала типа 3), и
оба переводят
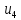 в
в
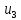 .
Мы выбираем b
и получаем сигнал baaba,
где b–допустимый
сигнал для
.
Мы выбираем b
и получаем сигнал baaba,
где b–допустимый
сигнал для
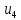 ,
а aaba
сигнал для
,
а aaba
сигнал для
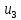 .
.
Время
сложности этого алгоритма O(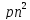 ),
а размер объявленного дерева O(
),
а размер объявленного дерева O(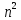 ).
).
Теперь произведем простой условный диагностический эксперимент для определения начального состояния. Эксперимент базируется на наблюдении за текущим множеством.
Алгоритм II (Простой Условный Диагностический Эксперимент):
Что нужно: Завершенное дерево ST (из I алгоритма).
Что получим: Простой условный диагностический эксперимент.
Метод:
I
и C
начальное и текущее множества, которые
согласовываются с наблюдаемым выходом
(изначально, I=C
равные всему набору состояний S).
Пока |I|>1
(и таким образом, |C|>1),
найдем низшую вершину u
дерева, чье обозначение содержит текущее
множество C.
Применяем входную последовательность
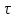 ,
связанную с u,
и изменяем I
и C
в соответствии с выходом.
,
связанную с u,
и изменяем I
и C
в соответствии с выходом.
Пример:
Рассмотрим автомат на рис.6, если мы
применим Алгоритм II
к дереву ST
на рис.8, получим простой условный
диагностический эксперимент на рис.7.
Сначала, подаем символ a
– обозначение корня. Допустим выход 0.
Тогда начальное множество I={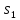 ,
,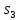 ,
, },
а текущее множество C={
},
а текущее множество C={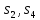 ,
,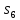 }.
Низшая вершина ST,
которая содержит C,
это
}.
Низшая вершина ST,
которая содержит C,
это
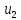 ,
тогда подаем последовательность из
,
тогда подаем последовательность из
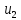 :
aba.
Пусть последний выход 1. Тогда начальное
множество I={
:
aba.
Пусть последний выход 1. Тогда начальное
множество I={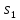 ,
,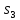 },
C={
},
C={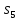 ,
,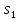 }.
Низшая вершина, которая содержит C,
это
}.
Низшая вершина, которая содержит C,
это
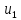 и подаем последовательность ba,
после которой мы узнаем начальное
состояние. Другие ветви последовательности
строятся аналогично.
и подаем последовательность ba,
после которой мы узнаем начальное
состояние. Другие ветви последовательности
строятся аналогично.
Алгоритм
II
имеет длину не больше n(n-1)/2
и строит простой условный диагностический
эксперимент за время O(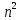 ),
имея готовое дерево.
),
имея готовое дерево.
