
Жданов Явления переноса в газах и плазме 2008
.pdf
f =1,77 γ − 0,45 . |
(5.35) |
5.7. Вязкость и теплопроводность газовых смесей
Элементарную теорию явлений переноса в случае вязкости и теплопроводности нетрудно обобщить на случай газовой смеси. Для произвольной газовой смеси, состоящей из N компонентов ( N типов молекул), тензор вязких напряжений и вектор теплового потока определяются простым суммированием по N
N |
N |
|
πrs = ∑παrs = −2ηSrs , |
η = ∑ηα , |
(5.36) |
α=1 |
α=1 |
|
N |
N |
|
q = ∑qα = −λ T , |
λ = ∑λα . |
(5.37) |
α=1 |
α=1 |
|
Здесь ηα и λα – парциальные коэффициенты вязкости и тепло-
проводности (не путать с соответствующими коэффициентами для чистых компонентов), η и λ – соответствующие коэффициенты
для смеси.
При получении линейных соотношений переноса и выражений для парциальных коэффициентов переноса можно использовать общее уравнение переноса элементарной теории (5.2), записав его для компонента α смеси,
Γα = − |
1 |
nα |
vα |
λα |
∂Gα |
. |
(5.38) |
|
2 |
∂x |
|||||||
|
|
|
|
|
|
Обобщая соответствующую процедуру вывода соотношений для тензора вязких напряжений и теплового потока в простом газе на
случай газовой смеси, для парциальных вязких напряжений παyx и
тепловых потоков qα получаем |
|
|
|
|
|
|
|
|||
π |
=−η |
duy |
, |
q |
|
= −κ |
|
dT |
, |
(5.39) |
|
|
α dx |
||||||||
αyx |
α dx |
|
α |
|
||||||
где
161
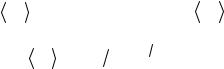
ηα = |
1 |
ραλα vα |
, |
κα = |
1 |
ρα cV αλα |
vα . |
(5.40) |
|
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||
Здесь ρα = mαnα , |
vα |
= (8kT πmα )1 2 , |
cV α –парциальная |
||||||
удельная теплоемкость при постоянном объеме, λα – средняя дли-
на свободного пробега частиц сорта α в смеси, определяемая выражением (4.70) главы 4.
Рассмотрим сначала вопрос о вязкости газовой смеси. Обозначим через ηαα коэффициент вязкости чистого газа, образованного из
молекул сорта α . Используя (4.70) и формулы для вязкости простого газа (5.4) – (5.5), для парциального коэффициента вязкости приходим к выражению
|
ηα |
= |
|
|
|
ηαα |
|
|
|
= |
|
|
|
|
ηαα |
|
|
|
|
|
. |
(5.41) |
|||||||
|
|
|
|
N |
ν |
|
|
|
|
|
N |
|
|
x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
αβ |
|
|
|
|
|
|
β |
|
|
|
|||||||||||
|
|
|
|
1+ ∑ |
|
|
1+ |
∑Gαβ |
|
|
|
|
|
||||||||||||||||
|
|
|
ναα |
|
xα |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
β=1 |
|
|
β=1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
β≠α |
|
|
|
|
|
|
|
|
β≠α |
|
|
|
|
|
|
|
|||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
αα |
= |
1 |
|
|
kT |
|
, |
|
|
G |
αβ |
= Ω(αβ0,1) |
|
|
, |
|
|
(5.42) |
||||||||||
|
|
|
|
|
|
|
(0,1) |
|
|
|
|
|
(0.1) |
|
|
|
|
||||||||||||
|
|
|
|
2π Ωαα |
|
|
|
|
|
|
|
|
|
|
Ωαα |
|
|
|
|
|
|
||||||||
где использованы соотношения (5.6) и (4.83). |
|
|
|
|
|
|
|
||||||||||||||||||||||
Для вязкости N -компонентной газовой смеси получаем |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
ηαα |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
η |
= ∑ |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
(5.43) |
|||||||
|
|
|
|
|
|
|
N |
|
|
|
xβ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
α=11+ ∑Gαβ |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
xα |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
β=1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
β≠α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражение для коэффициента вязкости смеси в форме (5.43), предложенное еще в 1904 г., известно как формула Васильевой. Многие последующие исследования, основанные на различных мо-
162

дификациях элементарной кинетической теории, являлись лишь попыткой дать более достоверные выражения для параметра Gαβ . Выражения (5.41) и (5.43) можно скорректировать, используя в качестве вязкостей чистых компонентов ηαα результаты строгой теории либо экспериментально определяемые величины. С другой стороны, для величины Gαβ в случае модели молекул – твердых
сфер, используя соотношения (4.86) – (4.87), получаем
Ω(1,1)
Gαβ = 2 (αβ ) . (5.44)
Ωαα2,2
Выразим это отношение через значения коэффициентов вязкости [ηαα ]1 и бинарной диффузии [Dαβ ]1 (см. следующий параграф), получаемые на основе строгой теории.
В результате
|
6 mα + mβ kT [ηαα ] |
|
||
Gαβ = |
|
p [Dαβ ]1 . |
(5.45) |
|
5 |
2mαmβ |
|||
|
|
|
1 |
|
Более обоснованный, хотя и приближенный результат Брокау (см. [11]), получается в результате разложения определителей, через которые записывается вязкость смеси в формулах строгой теории. В этом случае
|
6 |
|
kT [ηαα ] |
|
|
Gαβ = |
|
Aαβ |
|
[Dαβ ]1 . |
(5.46) |
5 |
mα p |
||||
|
|
|
1 |
|
|
Здесь Aαβ = Ω(αβ2,2)  Ω(αβ1,1) . С учетом слабого изменения величи-
Ω(αβ1,1) . С учетом слабого изменения величи-
ны Aαβ с температурой для модели Леннард-Джонса можно ис-
пользовать некоторое среднее значение величины (6 5)Aαβ =1,32 вместо 1,2 в формуле (5.46).
5)Aαβ =1,32 вместо 1,2 в формуле (5.46).
163

Заметим, что расчет вязкости смеси по формуле (5.43) с использованием (5.45) или (5.46) дает довольно близкие результаты, если массы частиц компонентов различаются не слишком заметно. В общем случае следует пользоваться более достоверным результа-
том (5.46).
На практике для расчета вязкости смеси на основе известных экспериментальных данных по вязкостям чистых газов и измеренных коэффициентов бинарной диффузии часто используется общая формула (5.43), в которой
Gαβ =1,385 |
kT |
ηαα |
. |
(5.47) |
|
pmα |
Dαβ |
||||
|
|
|
Здесь ηαα и Dαβ – экспериментально определяемые коэффициенты вязкости чистых газов и коэффициенты бинарной диффузии. Выражение для Gαβ в виде (5.47) было предложено Уилки и Бад-
денбергом [11,19] на основе обработки большого массива экспериментальных данных для двухкомпонентных смесей различных газов, в результате чего в выражении появился эмпирический коэффициент 1,385. Известна также формула Уилки [19], в которой фигурируют лишь вязкости чистых компонентов,
|
m |
|
1 2 |
|
|
|
|
1 2 |
|
1 4 |
2 |
|
|
|
|
|
|
|
m |
|
|
||||||
Gαβ = |
β |
|
|
|
+ |
|
ηαα |
|
β |
|
|
. (5.48) |
|
|
|
1 |
|
ηββ |
|
|
|
|
|
||||
|
8(mα + mβ ) |
|
|
|
mα |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Использованный выше подход можно применить и для получения соответствующих выражений в случае теплопроводности смеси. При этом парциальная теплопроводность компонента α определяется выражением
κα = |
|
καα |
|
|
|
|
|
|
N |
ν |
|
, |
(5.49) |
||
|
|
|
|||||
1 |
+ ∑ |
|
αβ |
|
|
|
|
ν |
αα |
|
|
|
|||
|
|
β=1 |
|
|
|
||
|
|
|
|
|
|
||
|
|
β≠α |
|
|
|
|
|
164

а для теплопроводности смеси опять приходим к выражению, аналогичному по своей структуре формуле для вязкости смеси,
N |
καα |
|
|
|
|
|
κ = ∑ |
|
|
|
|
||
N |
xβ |
, |
(5.50) |
|||
α=1 |
1+ ∑Hαβ |
|||||
xα |
|
|
|
|||
|
β=1 |
|
|
|
||
|
β≠α |
|
|
|
|
|
где καα – коэффициент теплопроводности чистого газа, образованного из молекул сорта α . Для одноатомных газов связь καα и ηαα в первом приближении строгой теории определяется соотношением
[καα ]1 |
= |
15 |
k |
[ηαα ]1 . |
(5.51) |
|
4 mα |
||||||
|
|
|
|
|||
В приближении, соответствующем элементарной теории, можно положить Hαβ = Gαβ , где Gαβ определяется выражением (5.45) либо (5.46). Выражение для H αβ , полученное Брокау (см. [11]) раз-
ложением соответствующих определителей, через которые записывается теплопроводность смеси в формулах строгой теории, оказывается существенно более сложным, чем соответствующее выражение (5.46) для вязкости. На практике для определения Hαβ часто
используется формула Мэзона-Саксены [11], в которой фигурируют теплопроводности чистых компонентов
|
m |
β |
|
1 2 |
|
|
[κ |
αα |
] |
1 2 |
|
1 4 2 |
|
||
H αβ =1,065 |
|
|
|
|
|
|
1 |
|
|
mα |
|
|
|
||
8(mα + mβ ) |
|
1 |
+ |
|
[κββ |
] |
|
|
mβ |
|
|
, (5.52) |
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
где коэффициент 1,065 вводится эмпирическим путем для улучшения согласия с экспериментом.
Приводимые выше выражения для теплопроводности смеси справедливы, вообще говоря, лишь для смеси одноатомных газов. Если в состав смеси входят газовые компоненты из двухатомных
165

либо многоатомных молекул, хорошим приближением при расчетах теплопроводности оказывается формула Эйкена-Гиршфелдера
[10]
N |
|
N |
x |
[D |
] |
−1 |
|
|
|
|
|||||
κ = κmon + ∑ncαint [Dαα ]1 |
1 |
+ ∑ |
xβα[Dαααβ ]1 |
|
. (5.53) |
||
α=1 |
|
β=1 |
|
|
1 |
|
|
|
|
β≠α |
|
|
|
|
|
При этом κmon вычисляется по формулам теории одноатомных газовых смесей, cαint – удельная теплоемкость, соответствующая внутренним степеням свободы молекул компонента α , [Dαα ]1 и
[Dαβ ]1 – соответственно коэффициенты самодиффузии и бинар-
ной диффузии, которые либо рассчитываются по известным формулам первого приближения Чепмена-Каулинга, либо берутся из эксперимента.
166

ГЛАВА 6. ДИФФУЗИОННЫЕ ЯВЛЕНИЯ В ГАЗОВЫХ СМЕСЯХ
Неравновесные явления в газовых смесях отличаются бόльшим разнообразием, чем в простом газе, поскольку наряду с вязкостью и теплопроводностью важную роль приобретают диффузионные явления. С пространственной неоднородностью концентрации компонентов смеси связано явление так называемой концентрационной диффузии, присутствие градиента давления вызывает бародиффузию, а наличие градиента температуры – термодиффузию. Как отмечалось в предыдущей главе, использование метода средней длины свободного пробега при рассмотрении диффузионных явлений в газовой смеси (за исключением самодиффузии) оказывается мало эффективным. Поэтому ниже мы используем другой подход, который можно назвать методом баланса импульса. Идея использования этого метода восходит еще к работам Максвелла и Стефана, интерес к его применению при анализе диффузии в газах возродился 50-х годах прошлого века (см. [26]), в кинетике газов и плазмы он использовался в работах Т. Каулинга [27] и Д.А.ФранкКаменецкого [7,28].
6.1. Метод баланса импульса. Сила диффузионного трения
Выделим в газе малый цилиндрический объем толщиной dx с поперечным сечением S (рис. 6.1).
dx
S
dp1
Рис.6.1
Сила, действующая на молекулы компонента 1 в этом объеме и связанная с наличием неоднородности парциального давления компонента вдоль оси X , равна, очевидно,
167

[p |
− (p |
|
)]S = −S dp |
|
|
dp |
|
|
+ dp |
= |
− |
1 |
Sdx |
||||
dx |
||||||||
1 |
1 |
1 |
1 |
|
|
|
В стационарном состоянии эта сила должна уравновешиваться силой диффузионного трения, действующей на молекулы компонента 1 со стороны молекул компонента 2. Природа этой силы связана с тем, что при столкновении разнородных молекул смеси происходит передача импульса от частиц компонента 1 частицам другого компонента. Средняя величина теряемого при столкновениях импульса, отнесенная к единице объема и единице времени, обозначалась выше как R1 и рассчитывалась в параграфе 4.10. Условие баланса
сил, вызванных наличием градиента парциального давления компонента и силы диффузионного трения, для объема Sdx в установившемся режиме диффузии может быть записано в виде
− dp1 Sdx + R1Sdx = 0
dx
или
dp1 = R |
|
|
dx |
1 . |
(6.1) |
|
|
|
Напомним, что выражение для R1 , получаемое с использованием
определенного приближения к функциям распределения молекул компонентов (4.74), имеет вид
R1 = −n1μ12ν12 (u1 −u2 ) , |
(6.2) |
где μ12 = m1m2 (m1 + m2 ) – приведенная масса молекул, |
ν12 – |
эффективная частота столкновений с передачей импульса (см.
формулу (4.78)).
Для того чтобы лучше уяснить физический смысл этого результата, мы дадим здесь еще один более простой вывод выражения для
R1 , используя модель твердых сферических молекул. Пусть z12 – число столкновений, испытываемых молекулой сорта 1 в единицу времени с молекулами сорта 2, а p1 – изменение импульса моле-
кулы 1 при одном таком столкновении. Полное изменение импульса молекулы сорта 1 в результате столкновений равно, очевидно,
168

z12 p1 . Соответствующее среднее изменение импульса получает-
ся усреднением по всем столкновениям. Примем для простоты, что среднее значение произведения двух величин можно приближенно заменить произведением средних, т.е. будем определять величину
R1 = z12  p1
p1 . Величину z12 положим равной средней частоте
. Величину z12 положим равной средней частоте
столкновений ν12(1) частиц сорта 1 с частицами сорта 2 , которая для модели молекул–твердых сфер определяется выражением (4.63)
ν(1) = n g πd 2 |
|
|
8kT |
1 2 |
|||
, |
g = |
. |
|||||
πμ |
|||||||
12 |
2 |
12 |
|
|
|
||
|
|
|
|
|
12 |
|
|
При усреднении p1 обращается в нуль та часть величины  p1
p1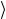 , которая связана с тепловым движением частиц, поэтому
, которая связана с тепловым движением частиц, поэтому  p1
p1 = m1
= m1 u1
u1 . Известно (см., например, [13, 21]), что для моле-
. Известно (см., например, [13, 21]), что для моле-
кул, представляемых в виде твердых упругих сфер, их рассеяние в результате столкновений оказывается изотропным в системе отсчета, связанной с их центром масс. Это означает, что в этой системе отсчета скорости упорядоченного движения молекул каждого сорта после столкновения равны нулю, а значит в обычной (лабораторной) системе отсчета обе эти скорости равны скорости центра масс G . Поскольку G = (m1u1 +m2u2 )/(m1 +m2 ), для среднего изменения
скорости u1 при столкновении имеем |
|||||
u1 |
= G −u1 |
= |
m2 (u2 −u1 ) |
|
|
m1 + m2 |
|||||
|
|
|
|||
или
p1 = μ12 (u2 −u1 ) .
= μ12 (u2 −u1 ) .
В результате средняя передача импульса в единичном объеме смеси от всех молекул сорта 1 молекулам сорта 2 определяется как
R |
1 |
= −n μ |
12 |
ν(1)(u |
1 |
−u |
2 |
) . |
(6.3) |
|
1 |
12 |
|
|
|
Как видно, различие между выражениями (6.3) и (6.2) проявляется в определении эффективных частот столкновений. Для модели
169

твердых сфер ν12(1) = (3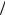 4)ν12 , т.е. результаты приближенного и строгого расчета отличаются лишь множителем (3
4)ν12 , т.е. результаты приближенного и строгого расчета отличаются лишь множителем (3 4).
4).
6.2. Концентрационная диффузия
Начнем анализ диффузионных явлений с вывода выражения для диффузионного потока, вызванного неоднородностью концентрации компонентов смеси. Ограничимся для простоты случаем бинарной смеси газов.
Напомним, что молярный диффузионный поток компонента 1 в смеси определяется выражением (3.58)
J m |
= n (u |
1 |
− um )= |
n1n2 |
(u −u |
2 |
) |
, |
m = − |
m . (6.4) |
|
||||||||||
1 |
1 |
|
n |
1 |
|
|
J2 |
J1 |
||
|
|
|
|
|
|
|
|
|
|
Запишем теперь уравнение баланса импульса для компонента 1 (6.1) с учетом выражения для R1 (6.2) в проекции на направление оси X
n μ ν |
(u |
−u |
|
)= − |
dp1 |
|
|
|
dx . |
(6.5) |
|||||
1 12 12 |
1 |
|
2 |
|
|||
Выражая отсюда разность скоростей компонентов, для молярного диффузионного потока (6.4) получаем
|
J m |
= −D |
dn1 |
= −nD |
dx1 |
. |
(6.6) |
|
|
|
|
||||||
|
1 |
12 |
dx |
12 |
dx |
|
||
Здесь |
использованы |
соотношение |
p1 = n1kT , |
определение |
||||
x1 = n1 |
n и предполагается, что полное давление p и температура |
|||||||
газа T |
поддерживаются постоянными. Коэффициент пропорцио- |
|||||||
нальности в выражении (6.6) соответствует коэффициенту бинар-
ной диффузии D12 |
и определяется выражением |
|
|
|||||||
|
D12 = |
n2kT |
3 |
|
kT |
|
|
|||
|
|
|
= 4 |
|
|
, |
(6.7) |
|||
|
nμ12 |
ν12 |
nμ |
g Q(1) |
||||||
|
|
|
|
|
|
12 |
12 |
|
|
|
где |
g = (8kT πμ |
|
)1 2 , а |
Q(1) |
– среднее эффективное сечение с |
|||||
|
12 |
|
|
12 |
|
|
|
|
|
|
передачей импульса (формула (4.79)). Удобно выразить |
D12 , ис- |
|||||||||
170
